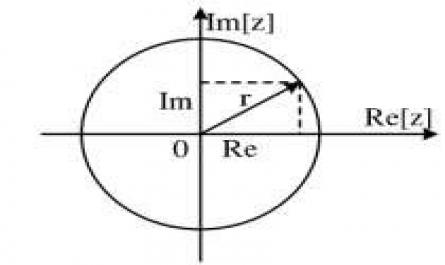
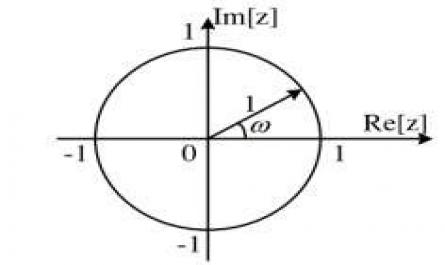
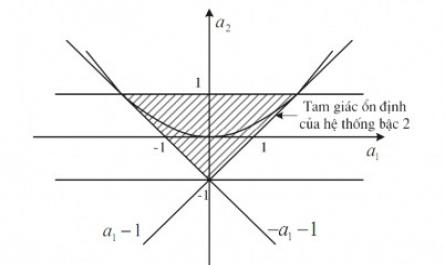
Xử lý tín hiệu số

Lời Nói Đầu Hiện Nay, Số Hóa Trong Lĩnh Vực Công Nghệ Thông Tin Và Công Nghệ Kỹ Thuật Điện - Điện Tử Đang Được Thực Hiện Trên Toàn Thế Giới Cũng Như Tại Việt Nam. Chính Vì Thế Xử Lý Tín Hiệu Số (Dsp- Digital Signal Processing) Đã ...

Tín hiệu số dễ dàng lưu trữ trên các thiết bị băng đĩa từ mà không bị mất mát hay giảm chất lượng. Như vậy tín hiệu số có thể truyền đi xa và có thể được xử lý từ xa. Phương pháp xử lý số cũng cho phép thực hiện các ...

Dãy x ( n ) có chiều dài: L [ x ( n )] = [0, 3] = 4 x  n  ` -2 -1 0 1 2 3 4 n Hình 1.22. Dãy có chiều dài hữu hạn N =4 c. Năng lượng của dãy Năng lượng của dãy x ( n ) được định nghĩa như sau:  Ví dụ 3: E x   n  x ( n ) 2 (1.8) Hãy ...

Chú ý: Tích chập này chỉ đúng với hệ thống tuyến tính bất biến vì nó được định nghĩa chỉ cho hệ thống này. c. Các tính chất của tích chập - Tính chất giao hoán y ( n )  x ( n )  h  n   h  n   x ( n )   (1.20) =  x ...

H ( n ) = 0 với mọi n < 0 (1.24) Định lý đảo: Nếu đáp ứng xung h ( n ) của một hệ thống tuyến tính bất biến bằng 0 với n < 0 thì hệ thống đó là nhân quả. Nhận xét: Các hệ thống nhân quả là hệ thống duy nhất thực hiện ...

Ví dụ 3: Giải phương trình sai phân tuyến tính hệ số hằng sau đây: y ( n )  2 y ( n  1 )  3 y ( n  2 )  x ( n )  2 x ( n  1 ) với kích thích x ( n )  u ( n ) và điều kiện ban đầu y ( - 1) = y ( - 2) = 0. Cho biết tính ổn định của ...

Ví dụ 4: Hãy vẽ sơ đồ cấu trúc của hệ thống rời rạc được cho bởi phương trình sai phân tuyến tính sau đây: y  n   b 0 x  n   a 1 y  n  1   a 2 y  n  2   a 4 y  n  4  Giải: Đây là phương trình sai phân ...

 1   n h 1  n    2 0  n  2   0 c¸c gi¸ trÞ cßn l¹i h  n   1   n  1   u  n  2   u  n  6  2 2 h  n   rect  n  3 11 Tìm đáp ứng xung h ( n ) của hệ thống tổng quát. Bài 1.21 Cho một hệ ...

Hình 2. 4.Vòng tròn đơn vị d. Cực và không (Pole và Zero) Trong thực tế chúng ta thường gặp các biến đổi Z cho dưới dạng một thương số của hai đa thức z (hoặc z -1 ) và như vậy X ( z ) là hàm hữu tỉ của z : - Định nghĩa không X ( z ) ...

Theo định lý Cauchy ta có: 1  n  m  1  1 víi n  m 2  j Ñ   z dz  0 víi n  m Với m = n ta có: C  x ( n )  1 Ñ  X ( z ) z ( n  1) dz (2.21) j 2  C Tích phân (2.18) chính là biểu thức của phép biến đổi Z ngược, nó được ...

Z Để đơn giản và dễ hiểu mà không làm mất đi tính tổng quát, giả sử X ( z ) dạng chính tắc và có r cực thực đơn z pk , một cực thực bội z pq bậc q , một cặp cực phức liên hợp z pe và * , khi đó có thể phân tích X ( z ) thành ...

Biến đổi Z của hàm tự tương quan r x (m) Nếu: Thì: ZT [ x ( n )]  X ( z ) x x R ( z )  ZT [ r ( m )]  X ( z ) X ( z  1 ) (2.52) 2.4. Ứng dụng biến đổi Z trong xử lý tín hiệu và hệ thống rời rạc 2.4.1. Hàm truyền đạt của hệ thống rời ...

1 1 X  z   X  z    z  1 X  z  Y  z   X  z   z  1 X  z    1  z  1  X  z  Từ đây ta có: 1 1 1 X  z   X  z  1 1   z  1 1  z  1 Y  z   X  z  1   z  1 1  Y  z ...

Thay điều kiện đầu: y   2    4 ; y   1    1 Ta có: 9 3   Y  z  1  3 z  1  2 z  2  1  2 z  1  8  X  z  3 9 X  z   3 2 1  1 z Biến đổi tiếp: 1  3 z  1 9 z  3 Y  z   z  1  ...

Bài 2.27 Cho hệ thống được mô tả bởi phương trình sai phân sau: y ( n )  0.7 y ( n  1)  0.12 y ( n  2)  x ( n  1)  x ( n  2) và tín hiệu vào x ( n )= nu ( n )? Xét tính ổn định của hệ thống? Tính đáp ứng của hệ thống? Bài 2.28 ...

Vậy : FT [2  n u ( n )]   1 1  2  1 . e  j   1 1  0,5 e  j  c.   ( n )  1 n  Hàm  ( n ) thoả mãn (3.16) nên tồn tại biến đổi Fourier :  FT [  ( n )]     ( n ). e  j  . n n   1. e  j  0 ...

Ví dụ: FT [ nx ( n )]=j dX (e j  ) d  (3.38) Hãy tìm biến đổi Fourier của dãy Giải : x ( n )  2  n n . u ( n ) Có : F T   2  n u  n     1 1  0,5 e  j  Theo (3.38) có : FT [ 2  n n . u ( n )]  d  1  j    0,5  . e ...

Chuyển tín hiệu và hệ thống rời rạc sang miền tần số rời rạc chúng ta dùng một công cụ toán học gọi là biến đổi Fourier rời rạc (Discrete Fourier Transform: DTF). 3.5.1 Biến đổi Fourier rời rạc đối với các tín hiệu tuần hoàn có chu ...

~ x 1 ( m ) 6 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 n ` ~ -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 n x 2 (  m ) 6 ` ` ~ ~ -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 n x 1 (0) 6 . x 2 (0) 6 ` ~ x 2 (1  m ) 6 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 n ` ` x 1 (1) 6 . x 2 (1) 6 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 n ~ ~ ` ~ ...

DFT  rect ( n )    N khi k=0  L N  0 khi 0<k  (N-1) Tức là : Vậy: D FT  r ect L ( n ) N   N .  ( k ) N  sin( k  L / N ) .e -j k  (L-1 ) khi N > L L N  DFT  rect ( n )    N sin( k  / N )  N.  (k) khi N = L  N 3.5.2.2. ...

X  n   x  n      1 2  1,1,1    thông qua biến đổi Fourier. Bài 3.13 Cho dãy tín hiệu:  1  n 2 x  n       u  n  Tìm j  Bài 3.14 X  z  và X  e j   Xác định mật độ phổ năng lượng S x ...

B. Bộ lọc thông cao lý tưởng Bộ lọc thông cao lý tưởng có đáp ứng biên độ được cho bởi:          c H  e j     1          0         c còn lại (4.2) Biểu diễn bằng ...

Nhận xét: - Nếu có bộ lọc số thông tất, bộ lọc số thông dải và bộ lọc chắn dải có cùng đáp ứng pha thì ta có quan hệ sau: j  j  j  H bs ( e )  H ap ( e )  H bp ( e ) j  j  j  H bs ( e ) : là đáp ứng tần số của bộ lọc ...

Đổi biến, đặt m   N  1  n   n   N  1  m  ,     2    2  Khi n = 0 thì m   N  1    2   Khi n   N  1   thì m =1, nhận được : 2  1      N  1  1  N  1    ...

J  dãy không nhân quả vô hạn. Khi dùng hàm cửa sổ để hạn chế h(n) trở thành đáp ứng xung h(n) N nhân quả và hữu hạn, thì đáp ứng biên độ tàn số H lp ( e ) của bộ lọc được  tổng hợp có dạng sườn dốc ở vùng tần số ...

  N  1  9  1  4   (  )   4  2 2 Đáp ứng xung của bộ lọc thông thấp lý tưởng pha tuyến tính: h lp ( n )  sin   ( n   )   c  ( n   ) sin   ( n  4) / 4   ( n  4) Bước 2 : Dùng cửa sổ hình ...

ĐÁP ÁN VÀ HƯỚNG DẪN GIẢI Đáp án chương 1 Bài 1.1 Theo định nghĩa dãy nhảy đơn vị và dãy xung đơn vị ta có:  u ( n )    ( n  k ) k  0  ( n )  u ( n )  u ( n  1) Bài 1.2 Ta xác định u  n  5  và u  n  2  sau đó ...

  n  h  n   16   Vậy hệ thống đã cho là ổn định Bài 1.23   1  n    h  n     3   víi n  0 Ta có:  0 víi n cßn l¹i h ( n ) < 0 với n < 0 nên hệ thống là nhân quả.    1  ...

X ( n )  4 n u ( n )  X ( Z )  Z Z  4 Z  4 Y ( Z ). Z 2  5 Z  6  Z 2 Z . Z  4 2 Z 2  Z  1 Z 2 Y ( Z )   2 Z  1  Z  1   A  B  C Z  Z  2  Z  3  Z  4   Z  2   Z  3   Z  4  A   2 Z ...

Vậy FT [ x ( n )]  1 1  ae  j  Bài 3.7 Với a=2: FT [ x ( n )]  1 1  2 e  j     a.  n  x  n      n  2 u (n)   1   n  0 x E  1 n  x  n    j  X 1  e  là không tồn tại  ...

3 ° X  k    x %  n  e n  0  j 2  nk 4 Mặt khác nếu biểu diễn x %  n  theo các hàm mũ phức: x %  n   A j 2  n e 4  A  j 2  n e 4 2 2 1 3 j 2  nk Và sử dụng : x %  n    ° X  k  e 4 N n  0  j 2  nk ...

Vẽ h  n  với  c 2   ,  c 1   và N = 7 2 3 sin    n  3   sin    n  3   h ( n )  1 2   2   n  3     1 3   3     n  3  2 3 h (3)  1  1  1 2 3 6 3 h (2)  h (4)  1  3 ...

N Vẽ sơ đồ bộ lọc x ( n ) 3 4π Z  1 1 2π Z  1 1 6 Z  1 1 2π y ( n ) 3 Z  1 4π Bài 4.20 Tương tự bài 4.19, sơ đồ bộ lọc như sau: 3 1 1 2π 1 6 1 2π 3 4π 4π Z  1  Z  1  Z  1  Z  1  x ( n ) y ( n ) Bài 4.21 Tương từ bài 4.20, ...