Xử lý tín hiệu số - 9

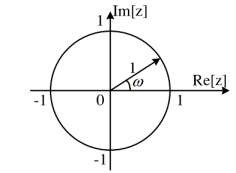
Hình 2. 4.Vòng tròn đơn vị

d. Cực và không (Pole và Zero)

Trong thực tế chúng ta thường gặp các biến đổi Z cho dưới dạng một thương số của hai đa thức z (hoặc z-1) và như vậy X(z) là hàm hữu tỉ của z:

- Định nghĩa không

X (z) N (z)

D(z)

(2.7)

Trong biến đổi Z nếu tại các điểm zor mà tại đó các không của X(z).

Có thể bạn quan tâm!

• Sơ Đồ Thực Hiện Hệ Thống Đệ Quy Và Không Đệ Quy
• Xử lý tín hiệu số - 7
• Biểu Diễn Tín Hiệu Và Hệ Thống Rời Rạc Trong Miền Z
• Các Phương Pháp Biến Đổi Z Ngược
• Định Lý Giá Trị Đầu Của Dãy Nhân Quả
• Ứng Dụng Biến Đổi Z Trong Xử Lý Tín Hiệu Và Hệ Thống Rời Rạc

Xem toàn bộ 272 trang tài liệu này.

Xzor 

thì các điểm đó gọi là

Vậy nghiệm của tử số N(z) chính là không của X(z).

Nếu N(z) là đa thức của z bậc M thì X(z) có M không.

- Định nghĩa cực

Trong biến đổi Z nếu tại các điểm

gọi là các cực của X(z).

zpk

mà tại đó

X zpk thì các điểm đó

Vậy nghiệm của mẫu số D(z) chính là cực của X(z).

Nếu D(z) là đa thức của z bậc N thì X(z) có N cực

- Biểu diễn X(z) dưới dạng cực và không

Nếu N(z) là đa thức của Z bậc M, D(z) là đa thức của z bậc N thì ta có thể viết:

N (z) b b z1 b z2  ... b zM

(2.8)

X (z) 0 1 2 M

D(z) a a z1 a z2  ... a zN

0 1 2 N

bM(z z01 )(z z02 )...(z z0M )

aN(z zp1 )(z zp2 )...(z zpN )

M M

(2.9)

b z z0r z z0r 

M r 1 Cr 1

a N N

N z zpk k 1

z zpk k 1

Ta cũng có thể biểu diễn X(z) theo đa thức của z-1

M

M

M

1

1

z 1z0r z 1z0r z 

(2.10)

N N

X z Cr 1CzM N r 1

z N 1z z1 1z z1 

k 1

pk pk

k 1

Trên mặt phẳng phức, các không điểm z0k của hàm X(z) được ký hiệu bằng dấu khuyên tròn nhỏ “o” còn các cực điểm zpr được ký hiệu bằng dấu gạch chéo nhỏ “x” như trên hình 2.5.

Imz

x

zp1

z

01

0

z x

z

02

Rez

p 2

Hình 2. 5. Không và cực của X(z).

Ví dụ :

Cho

xnanun

a  0

Hãy tìm ZT x n , RC X z , các không, các cực và vẽ chúng trên mặt phẳng Z.

Giải:

Từ định nghĩa biến đổi Z ta có:

ZT xnX z





n



anunzn 

n0

az1 n  1



1az1

với z a

Vậy

RC Xz:z

a, Rxa

X(z) có một không

z01  0 và một cực

zp1 a

Im[z]

1

a

x

1 1

1

z01

Re[z]

zp1

Hình 2. 6. Miền hội tụ của X(z) và vị trí cực, không với a>0.

2.2.2 Sự tồn tại của biến đổi Z

a. Định nghĩa miền hội tụ của biến đổi Z

Định nghĩa 1: Tập hợp tất cả các giá trị của z mà tại đó chuỗi



X z

xnzn ZT xn

n

hội tụ được gọi là miền hội tụ của biến đổi Z hai phía.

Ký hiệu: RC hoặc ROC: miền hội tụ (Region of Convergence) Đối với biến đổi Z một phía chúng ta cũng có định nghĩa tương tự: Định nghĩa 2: Tập hợp tất cả các giá trị của z mà tại đó chuỗi



X1zxnzn ZT1xn

n0

hội tụ được gọi là miền hội tụ của biến đổi Z một phía.

Ví dụ 1:

Cho tín hiệu rời rạc sau:

2

n

x n

víi

n 2

0 víi n cßn l¹i

Hãy xác định biến đổi Z hai phía, một phía và xác định miền hội tụ của chúng.

Giải:

xn

`

4

2

1

Tín hiệu x(n) là không nhân quả có chiều dài biểu diễn đồ thị trên hình 2.7.

L x n, 2; x(n) được

n

Hình 2. 7. Tín hiệu x(n) trong ví dụ 1.

Theo định nghĩa ta có biến đổi Z hai phía như sau:

 2 1

X(z) xnzn 2nzn  4z2  2z1 12nzn

n

Đổi biến n = -m ta có:



n

n

X (z) 2m zm 4z2  2z1 1

m1

Gọi:



m m

21 z z

X1 (z) 2

m1

z 

1 21 z 2 z

z  2

2 1

X2 (z)  4z  2z 1

z  0

Vậy:

X (z) 

z

2 z

 4z2  2z1 1

z  2;

z  0

Như vậy miền hội tụ của X(z) là miền nằm bên trong vòng tròn có bán kính là 2 trừ gốc tọa độ.

Im[z]

Mặt phẳng z

r=2

0 Re[z]

Miền hội tụ của X(z)

Hình 2. 8. Miền hội tụ của X(z) trong ví dụ 1.

Biến đổi Z một phía của x(n):

 2

X1(z) xnzn 2nzn  4z2  2z1 1

n0 n0

Vậy miền hội tụ của biến đổi X1(z) là toàn bộ mặt phẳng Z trừ gốc tọa độ z = 0.

b. Tiêu chuẩn Cauchy

Phát biểu tiêu chuẩn Cauchy

Chuỗi số vô hạn :





n0

x(n)

(2.11)

hội tụ nếu điều kiện sau được thỏa mãn:

1

(2.12)

lim x(n) n  1

n 

tách

Để sử dụng tiêu chuẩn hội tụ Cauchy xác định miền hội tụ của chuỗi (2.7), phải

X (z) thành hai chuỗi như sau:

1 

X (z) x(n).zn x(n).zn

X1(z) X 2

(z)

Trong đó :

n

n0



1

X1 (z) 

0

x(n).zn 

x(n).zn x(0)

(2.13)

Và:

n



X 2 (z) 

n0

n

x(n).zn

(2.14)

Theo tiêu chuẩn Cauchy, chuỗi

X 2 (z) sẽ hội tụ nếu thỏa mãn điều kiện:

1

lim

n 

x(n). zn n  1



Nếu tồn tại số

1

z1 lim x(n) n  1

n 

Rxhữu hạn để:

1

(2.15)

lim

n 

x(n) n

Rx

Thì :

Rx

| z1 |  1

Khi đó chuỗi

X 2 (z) sẽ hội tụ với mọi z thoả mãn điều kiện:

| z | Rx

(2.16)

Để tìm miền hội tụ của

X1 (z) , đổi biến đặt m n



thì chuỗi (2.10) được đưa

về dạng:

X (z) x(m).zm x(0)

1

m0

Nếu x(0) hữu hạn thì chuỗi

X1 (z)

sẽ hội tụ nếu thỏa mãn điều kiện :

1 1

lim

m 

x(m). zmm

 1

| z | .lim | x(m) | m m 

 1

11

Nếu tồn tại số

Rxhữu hạn để:

lim

m 

x(m) m



Rx

Thì : 1 | z |  1

Rx

Trong đó,

Rx

lim

m 

1

1

x(m) m

Hay trở về biến n:

1

Rx 

lim x nn

(2.17)

Khi đó chuỗi

X1 (z) sẽ hội tụ với mọi z thoả mãn điều kiện:

| z | Rx

(2.18)

RC Xz

là giao các miền hội tụ của

X1 (z)

theo (2.14) và

X 2 (z)

theo (2.12):

Nếu

RxRxthì

RC X z : Rx

z Rx.

Như vậy, dãy không nhân quả vô hạn x(n) có

X (z) ZT[x(n)]với miền hội tụ

là hình vành tròn trên mặt phẳng phức, có tâm là gốc tọa độ, bán kính trong

Rx, bán

kính ngoài

Rxnhư ở hình 2.7a . Các bán kính hội tụ

Rxvà

Rxđược xác định theo

(2.11) và (2.13) tương ứng. Nếu

Rxkhông hữu hạn hoặc

RxRxthì

X (z) không

xác định với mọi z, nên trong trường hợp đó dãy không nhân quả x(n) không có biến đổi Z.

Im[z]

R 

x

R 

Re[z]

x

Im[z]

Re[z]

R 

x

Im[z]

R 

x

Re[z]

a. Dãy không nhân quả. b. Dãy nhân quả. c. Dãy phản nhân quả.

Hình 2. 9. Miền hội tụ của biến đổi Z.

Khi x(n) là dãy nhân quả thì biến đổi Z của nó có thành phần

X1(z) 0 , nên

X (z) X2 (z) , do đó miền hội tụ của X (z) là miền hội tụ của X 2 (z) theo (2.12), nên

RC Xx:z

Rx.Miền này nằm ngoài vòng tròn tâm ở gốc tọa độ, đường kính

Rxnhư ở hình 2.7 b. Bán kính hội tụ

Rxđược xác định theo (2.11). Nếu

Rx thì

X (z) không xác định với mọi z, nên trong trường hợp đó dãy nhân quả x(n) không có biến đổi Z.

Khi x(n) là dãy phản nhân quả thì biến đổi Z của nó có

nên X (z) X1(z) , do đó miền hội tụ của X (z) là miền hội tụ của X1 (z)

X2 (z)  0 ,

theo (2.14),

nên RC X z  :| z | Rx. Đó là miền nằm trong vòng tròn tâm ở gốc tọa độ, đường kính Rx+ như ở hình 2.7c . Bán kính hội tụ Rx+ được xác định theo (2.13). Nếu = 0 thì

X (z) không xác định với mọi z, nên trong trường hợp đó dãy phản nhân quả x(n) không có biến đổi Z.

Biến đổi Z một phía có dạng giống với biến đổi Z hai phía của các dãy nhân quả, do đó miền hội tụ của biến đổi Z một phía là :

RC X1z:z

R 

x

Đó là miền nằm ngoài vòng tròn tâm là gốc tọa độ, đường kính

Rxnhư ở hình

2.7 b. Bán kính hội tụ

Ví dụ 2:

Rxđược xác định theo (2.11)

Cho

3 n

4

x(n) 



với mọi n

Hãy tìm biến đổi Z hai phía và miền hội tụ.

Giải:



3 n

ZT xnX z



n4 

zn

n

n n



nÒu n 0 nÒu n 0

Ta có:



n

3 n

1 3 1 

X (z) 

n0 4

z1 





n4 

z1 



Gọi:

3 n 1 3

X1 (z) 4

z1 

3 1

với

z1  1

4

n0 

 1

1 3 z1

4

1z

3

4

với

z 3 ;





4

Rx4

1 

31 

3

1 l 3z3









X 2 (z) 



n

4 

z1 

4 

 4

3

với

z  1

4

n

3 z

l1 

1z

z

4

4

 4

1 3 z

4

với

z 4 ;

3

Rx3

3 2

1 4 3 4

X (z) X

(z) X (z) 

với z 

1 2 3 1 3  4 3

14 z 14 z 



Miền hội tụ của X(z) cho trên hình 2.10 là hình vành khăn với bán kính trong

3

Rx4

và bán kính ngoài 4

3

mặt phẳng Z

Im[z]

Rx

Rx

Re[z]

Hình 2. 10. Miền hội tụ của X(z)

2.2. Biến đổi Z ngược

2.2.1. Định nghĩa biến đổi Z ngược

Nếu biến đổi Z thuận cho phép tìm hàm ảnh X(z) từ dãy gốc x(n), thì biến đổi Z

ngược cho phép tìm dãy gốc x(n) từ hàm ảnh X(z).



Để tìm biểu thức của biến đổi Z ngược, xuất phát từ biểu thức của biến đổi Z thuận:

X (z) x(n) zn n

và định lý Cauchy về tích phân theo chiều dương trên đường cong khép kín C

bao quanh gốc tọa độ trong mặt phẳng phức:

1 n1

1 víi n 0

(2.19)

2j Ñ

z dz 

0 víi n 0

C 

Nhân cả hai vế của biểu thức với thừa số

z(m1)

j2, rồi lấy tích phân theo

chiều dương trên đường cong kín C nằm trong miền hội tụ của X(z) và bao quanh gốc tọa độ, nhận được:

1 (m1) 1 

n ( m1)

(2.20)

j2

ÑX (z)z dz 

j2Ñ

x(n)z z dz

C C n

Vì tích phân lấy trong miềm hội tụ của X(z), nên có thể đổi vị trí của dấu tổng và dấu tích phân ở vế phải của (2.17):

1 (m1) 

1 ( nm1)

j2

ÑX (z)z dz x(n)

j2

C n

Ñz dz

C