Xử lý tín hiệu số

x(n)  4n u(n) X (Z ) 

Z  4

Z  4

Y (Z ).

Z 2  5Z  6 

Z 2

Z .

Z  4

2Z 2 Z 1

Có thể bạn quan tâm!

Xem toàn bộ 272 trang tài liệu này.

Z 2

Y (Z )2Z 1Z 1ABC

Z Z  2Z  3Z  4Z  2Z  3Z  4

A 2Z 1Z 1

Z  3Z  4

B 2Z 1Z 1

Z  2Z  4

C 2Z 1Z 1

Z  3Z  2

Z  2

Z  3

Z  4

9

20

35

Y (Z ) 9 Z

 20 Z

 35 Z

Z  4

2 Z  2

Z  3 2

Z  4

y(n) 9 2n  20.3n 35 .4n u(n)

2 2 

Bài 2.16

a. Áp dụng:



brZr

H (Z ) r 0

akZk k 0

Y Z  1Z 2

H Z X Z 1 a Z 1 a Z 2 Z 2 a Z a

1 2 1 2

b. Ứng dụng tiêu chuẩn Jury ta có:

1. D(Z ) Z 1  1a1 a2  0 a2 1a1 

2. D(Z ) Z 1  1a1 a2  0 a2 1a1 

(vì N chẵn)

3. 1 a2 1 a2 1

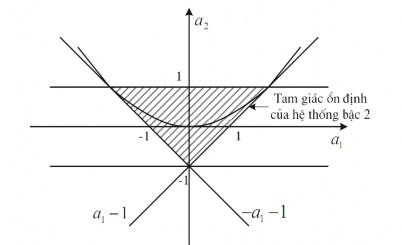
Bài 2.17

X z13z1 2z2

Miền hội tụ: toàn bộ mặt phẳng z, trừ z = 0.

X zcó hai không tại z

1;

z 2

và một cực kép tại z = 0

Bài 2.18

01 02

H ZH ZH Z1 H Z

1 2 3 

b' Z1 Z 1 

b' Z 1 11 

0

1 b'Z 1 b

b Z 1 b Z 3 b Z 6 

1 a Z 2 a Z 3 

Bài 2.19

1 0 1 2 3 1 2

Y (Z ) 1Z 1 Z 1 Z 1

Bài 2.20

H (Z ) 

X (Z ) 1Z 1 Z Z Z 

2z2

X (z) 

(1 0.5z1 )(1z1 )

X (z)  4 

1z1

 8

1 0.5z1

Miền hội tụ RC: |Z|>1

x(n)  4(n)  4(1)n u(n)  8(5)n u(n)

Bài 2.21

Công thức biến đổi Z

X (z) 

1 n n

n5 ( 2) z

X (z) 

1 l 5

l 5

15

5 1 l l

l 0 ( 2) z

l 0 ( 2) z

( ) z

1 5 5

1 1 l

( ) z

l 0 ( 2 z )

 ( 1 )5

z5

1

1z1

RC:

Bài 2.22

Đặt

z 1

x1(n) cos(0n)u(n)

x (n) 1 [e j0nu(n) ej0nu(n)]

1 2

1 1 1

 1z1cos()

X1 (z) 

[

2 1e

j0 z

1 

1e

j0 z

1 ]

1 2z1cos() z2

RC: |Z|>1

x(n) an x (n)

1

X (z) X1(a z)

1az1cos()

X (z)  0

Bài 2.23

1 2az 1cos() a2 z2

với |z|>|a|

1 2

x(n)  (an an )u(n) anu(n) anu(n) x (n) x (n)

X1 (z) 

1az1

RC: | z || a |

X 2 (z) 

1a1z1

RC: | z || 1 |

Vậy

X (z) 

1az1

 1

1a1z1

RC: | z |max(| 1 |,| a |)

Bài 2.24

Y (z) 

13 z1 1 z2

4 8

X (z)

Đáp ứng xung: X(z)=1

H (z) 

11 z1

 1

11 z1

2 4

h(n) 

1 n  1 n

[2( ) ( ) ]u(n) 2 4

Tính đáp ứng đối với dãy nhảy đơn vị Dãy nhảy đơn vị có biến đổi Z:

X (z) 

1z1

8 1

Y (z)  3

1z1

11 z1

 3

11 z1

2 4

y(n)  [8 

1 n  1 1 n

Bài 2.25

2( ) ( ) ]u(n)

3 2 3 4

Tìm X1(z), X2(z)

1 1

X (z) 1 ( ) n z n  ( )z n

1 n2 n0 3

1 1 n n

1 l l 1 l l

Tìm

n( 2) z

= l 1 ( 2) z = l 0 ( 2) z 1

= 1

11 z

1 =

z1 1

RC: |z|<2

Tính





n0

( )z

n =

11 z1

RC:| z |1

X (z)  2 

1 z1 1

11 z1

 6

(11 z1 )(11 z)

RC: 1 | z | 2

2 3 3 2

 1

X (z) 

1 n n

11

Tìm y(n)

n0 ( 2) z

1 z

4

RC: |z|>1/2

Y (z) 

2

11 z1

 3

11 z1

 3

1 2z1

3 2

 1 n

10 1 n



y(n) 

2( )

 ( )

3 2

, n  0

Bài 2.26

4 (2)n ,

 3

n  0

(1z1 )(1z1 z2 ) 1

H (z) 

(1z1 )(1

1z1 )(11

2 5

z1 )

| z | 1

H (z) 

(1

1z1 z2

1z1 )(11

2 5

z1 )

1 | z | 1

9  3 z

H (z)  1 10 10 1

(z 1 )(z 1)

z 1

B

z 1

2 5 2 5

9  3 z

A Y (z)(z  0.5) |

z1/2

 5 / 2

trong đó Y (z)  10 10

(z 1 )(z 1)

2 5

B Y (z)(z  0.2) |z1/5 2.8

H (z)  1 [ 2

11 z1

2.8

11 z1

]z1

2 5

h(n) (n) 

1 n  1 n

[5( ) 14( ) ]u(n)

2 5

Bài 2.27

z1 z2

Y (z) X (z)

1 0.7z1  0.12z2

x(n) nu(n)

z1

X (z) 

(1z1 )2

Y (z) 

z2 z3

(1z1 )2 (1

z1 )(1

10 5

z1 )

Các điểm cực nằm trong vòng tròn đơn vị, vậy hệ thống ổn định

y(n)  [4.76n 12.36 

3 n  2 n

26.5( ) 38.9( ) ]u(n)

10 5

Bài 2.28

Biến đổi Z một phía của phương trình ta được:

Y1 (z) 5[z1Y1 (z) y(1)]  6[z2Y1 (z) z1 y(1) y(2)] X 1(z) 1 [z1 X 1(z) x(1)]

Với y(n)=0 khi n<0 và x(-1)=1/2 thay vào phương trình trên ta có:

Y1 (z)[1z1  6z2 ] X 1 (z)[11 z1 ] 1

2 4

(*)

Với

x(n)  2n , có

X 1 (z) 

z  2

thay vào (*) được:

1 5z

Y (z) 

4(z  2)(z  3)(z  2)

[ + + ]

Y1 (z)  1 A B C

z 4 z  2 z  3 z  2

A=1, B=9, C=-5

Y (z) 1

z  9

z  5 z

4 z  2 4 z  3 4 z  2

y(n) 1 2n u(n) 9 (3)n u(n) 5 (2)n u(n)]

4 4 4

Đáp án chương 3 Bài 3.1

j

a. X1e =1

jj

b. X 2 e e

 1 n1

c. X3

e jejn 

n0  2 

1 1 ej

n n

d. X 4

ej2ejn 2ej

n0 n0

Chuỗi này không tồn tại vì 2ej

Bài 3.2

 2 1. Vậy

x4 n

không có FT.

x2 n

Ta phân ra làm 2 trường hợp n < 0 và n > 0 ứng với các tín hiệu như vậy ta có kết quả:

x1 nvà

X X1 X 2 

Bài 3.3

 1a2

1 2a cosa2

L1

X e jAejn A

n0

jL1

1ejL

1ej

j 2 

sin(L/ 2)

X e

Ae



sin(/ 2)

Với  0 , biến đổi ta có:

X e j 0 

A L.

Phổ biên độ của

x ncó dạng:

A

A L

 0

Bài 3.4

X e j 0 





sin L / 2

sin / 2

Hàm phần thực và ảo

X (e j) cos(2).cos() - jcos(2).sin()

Hàm phần thực: Hàm phần ảo:

X R () cos(2).cos()

X I ()  - cos(2).sin()

Hàm độ Modul và Argument

Modul: Rút gọn:

Argument:

X (e j) 

cos2 (2).cos2 () + cos2 (2).sin2 ()

X (e j) cos(2)

 cos(2).cos() 

() arctg  cos(2).sin()



Rút gọn

() 

Hàm độ lớn và pha

Hàm độ lớn:

A(e j) cos(2) )

Bài 3.5

Hàm pha:

()=-- 

21



cos(2)

cos(2) 



N 1

FT x nX e jejn

n0

 1 e

j N

jN



jN

e 2

jN

e 2

1 ej

j 

e 2 e

j 

e 2

sin N

sin N

jN 1

e 22 sin 

X e j

2 sin 

sin N

arg X e jN 1arg  2 



2



 sin 

 2 

21

sin N

sin N

Với:



arg  2k 

 sgn  2



1

 sin 

 2 



 sin

 2







Bài 3.6

sin N Ae j 2

sin 

e jN 1



ZT x(n)

n



an .u(n).zn 

n0

az1 n

, z

1

1 a

ZT x(n)

1az



, z a

Nếu a  1 , RC[ZT[x(n)]] không chứa đường tròn đơn vị

=> FT[x(n)] không tồn tại

Nếu a  1, RC[ZT[x(n)]] chứa đường tròn đơn vị

Z e

=> FT[x(n)] tồn tại

Ta có:

FT x(n)X (z) j