Các Phương Pháp Biến Đổi Z Ngược

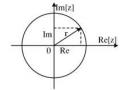
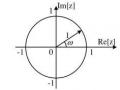
Theo định lý Cauchy ta có:

1 nm1

1 víi n m

2j Ñ

z dz 

0 víi n m

Với m = n ta có:

C 

Có thể bạn quan tâm!

Xem toàn bộ 272 trang tài liệu này.

x(n)  1 ÑX (z)z(n1)dz

(2.21)

j2C

Tích phân (2.18) chính là biểu thức của phép biến đổi Z ngược, nó được ký hiệu như sau:

Hay :

IZT[X (z)] x(n)

X (z) IZT x(n)

(2.22)

(IZT là chữ viết tắt của thuật ngữ tiếng Anh: Inverse Z Transform).

Khi ứng dụng biến đổi Z để giải các bài toán phân tích và tổng hợp hệ xử lý số, cần sử dụng biến đổi Z thuận để chuyển dãy x(n) sang miền biến số Z. Sau khi thực hiện những biến đổi cần thiết trong miền Z, cần sử dụng biến đổi Z ngược để nhận được kết quả trong miền thời gian.

Tìm biến đổi Z ngược để xác định dãy x(n)bằng cách tính trực tiếp tích phân thường rất phức tạp, vì thế người ta xây dựng các phương pháp gián tiếp sau để tìm biến đổi Z ngược :

- Phương pháp thặng dư.

- Phương pháp khai triển X(z) thành chuỗi lũy thừa.

- Phương pháp phân tích X(z) thành tổng các phân thức tối giản.

2.2.2. Các phương pháp biến đổi Z ngược

a. Phương pháp thặng dư

Trong lý thuyết thặng dư của hàm biến số phức thì tích phân vòng trong biểu thức biến đổi Z ngược có thể được đánh giá bằng tổng các thặng dư như sau:

Ñ

x n1

j2C

X(z)zn1dz Re s Xzzn1





zz pk 

(2.23)

Ở đây zpk là các cực của X (z)zn-1 nằm trong đường cong khép kín c.

Ta biểu diễn

X zzn1 dưới dạng sau:

X (z)zn1 (z)

(2.24)

(z zpk ) k



Re s Xzzn1



zz pk 

đọc là thặng dư của

X zzn1 tại cực z= zpk.

X zzn1 có

bao nhiêu cực thì phải có đủ bấy nhiêu thặng dư, sau đấy lấy tổng của tất cả các thặng dư này ta sẽ có x(n).

Công thức tính thặng dư của

X zzn1 như sau:



Re s X zz

n1

zz





pk 

z zpk

(2.25)

(s 1)!

d( sk 1)(z)

dz( sk 1)

Trong trường hợp riêng, nếu là nghiệm đơn thì biệt sau:

sk  1thì biểu thức có dạng đặc



Re s X zzn1

(z)

zz 

z zpk (zpk )

(2.26)

Sau khi tính tất cả các thặng dư của hàm

X zzn1 ở tất cả các cực trong đường

cong khép kín C và cộng chúng lại ta thu được x(n).

Ví dụ 1:

z 



Hãy tìm

Giải:

x(n) IZT[ X (z)] (z a) 

với

RC Xz:z a

Có X (z)z

(n1)

z.z(n1) zn

(z a) (z a)

Với

n  0 ,

X (z).z

(n1)

zn

(z a)

có cực đơn

zp a và

(z) zn .

Re s Xzzn1

(a) an

zz 



x(n)  Re s Xzzn1

n

a

zz pk 

khi n 0

VìRC Xz:z

a nên x(n) là dãy nhân quả, do đó kết quả là :



x(n) IZT z anu(n)

Ví dụ 2:

Cho:

X (z) 

 (z a) 

với

RC X z : z

b ;

a2 b2

(z2  2az b2 ) 

Hãy tìm biển đổi Z ngược.

Giải:

Ta có:

X (z)z

(n1)

zn

(z2  2az b2 )

. Với

n  0 , hàm X (z).z(n1) có hai điểm cực là

nghiệm của phương trình :

z2  2az b2  0

(b2 a2 )

jp

Vì a2 b2



0 , nên phương trình trên có hai nghiệm là cặp

a2 b2

số phức liên hợp :

zp1 zp

a j

 | zp | .e

và :

z z*

a j

 | z

| .ejp

(b2 a2 )

p2 p p

a2  (b2 a2 )

(b2 a2 )



Với : | z | 

b và arctg 

Theo các cực điểm z và z*

có thể phân tích



X (z)z(n1)

a 

thành :

X (z)z

p p

(n1) z

+ Với cực z p

(z z

có .

)(z z* )

Theo biểu thức thặng dư tìm được:

Re s X zz

n1

z z

1 (zp )

1 (zp ) 

(zp )

p 

zz p

(zp zp )



 | zp | .e 

jp n

a j (b2 a2 ) a j (b2 a2 ) 







Vậy:

Re s X zz

2 j (b2 a2 )



n1





zz p 

bn .e jnp

+ Với cực z p có 2 (z) (z z

, theo biểu thức thặng dư tìm được :

)

(z* )n

Re s X z zn1 

(z* ) p

z z p 

2 p (z* z )



p p

a j (b2 a2 ) a j (b2 a2 ) 







 | zp

| .ejpn

Vậy:

Re s Xzzn1



zz*

bn .ejnp

2 j (b2 a2 )



Ta có:

x(n)  Re s Xzzn1  Re s Xzzn1 

zz p 

2 j (b2 a2 )

bn .e jnp





bn .ejnp

zz p 

bn e jnp ejnp 

bn .sin(n)

(b2 a2 )

x(n) 

p

(b2 a2 )

2 j 

VìRC Xz:z

b nên x(n) phải là dãy nhân quả, do đó kết quả là :

z 

bnu(n) 



(b2 a2 )

IZT  (z2  2a.z b2 ) 

sin n arctg a

(b2 a2 )



Trong đó,

a2 b2 và

RC Xz:z b

b. Phương pháp khai triển thành chuỗi lũy thừa

Tổng quát X(z) là hàm giải tích của z, nên trong miền hội tụ của nó ta có thể

khai triển X(z) thành chuỗi lũy thừa của theo dạng:

zn



X (z) 

n

a zn

(2.27)



Mặt khác, theo định nghĩa của biến đổi Z có :

X (z) x(n).zn n

Trong miền hội tụ của X(z), cả hai chuỗi trên đều hội tụ nên khi đồng nhất các hệ số của hai chuỗi này ta tìm được dãy:

x(n) an

(2.28)

Vậy khi khai triển X(z) thành chuỗi luỹ thừa thì các hệ số của z-n chính là các giá trị của x(n).

Ví dụ 3:

Cho:

X (z) 

(z a)

Hãy tìm x(n) với các miền hội tụ của X(z) trong hai trường hợp:

a. Với

b. Với

Giải:

RC Xz:z a RC Xz:z a

a. Chia cả tử số và mẫu số cho z nhận được :

X (z) z 1

VìRC Xz:z

(z a) (1a.z1)

a nên x(n) là dãy nhân quả .

Chia tử số cho đa thức mẫu số (1 + az-1) :

1 | 1 + az-1 _

1 + az-1 1 - az-1 + a2z-2 - a3z-3 + a4z-4 - ......

- az-1

- az-1 - a2z-2

+ a2z-2

+ a2z-2 + a3z-3

- a3z-3

Tổng quát ta có:

X(z) =



X (z) 2

n0

zn

với z a

Vậy ta thu được dãy x(n) như sau:

x(n)  (a)n u(n)

với

RC Xz:z a

b. Với

RC Xz:z

a thì x(n) là dãy phản nhân quả

Hàm X(z) phải là chuỗi luỹ thừa của zn .

Chia tử số cho đa thức mẫu số (az-1 + 1) .

1 | az-1 + 1 _

1 + a-1z a-1z - a-2z2 + a-3z3 - a-4z4 + ......

- a-1z

- a-1z - a-2z2

+ a-2z2

+ a-2z2 + a-3z3

- a-3z3

- a-3z3 - a-4z4

+ a-4z4

...................

Tổng quát ta có:



X (z) (a)m zm m1

Để có dạng của biến đổi Z với lũy thừa z-1, ta đổi biến số m = -n

Ta có:



X (z) (a)nzn n1

Ta thu được dãy x(n) như sau:

x(n) (a)n u n 1

Từ ví dụ trên có các nhận xét sau:

với

RC Xz:z a

- Cùng một hàm X(z) nhưng với hai miền hội tụ khác nhau sẽ nhận được hai hàm x(n) khác nhau, điều đó có nghĩa là quan hệ giữa hàm X(z) và hàm x(n) của biến đổi Z hai phía chỉ là đơn trị khi ứng với một miền hội tụ xác định. Vì thế, để tìm biến đổi Z ngược của biến đổi Z hai phía, cần phải biết miền hội tụ của hàm X(z).

- Trong ví dụ, chuỗi lũy thừa biến đổi có quy luật nên tìm được biểu thức của số

hạng tổng quát an

và biểu thức của hàm x(n). Trong đa số các trường hợp, khi chia đa

thức để khai triển X(z) thành chuỗi lũy thừa, không thể tìm được quy luật biến đổi của chuỗi lũy thừa, nên chỉ tìm được giá trị một số mẫu của hàm x(n). Đó chính là nhược điểm cơ bản của phương pháp khai triển X(z) thành chuỗi lũy thừa, và vì thế phương pháp này ít được sử dụng.

c. Phương pháp khai triển thành phân thức tối giản

Trong thực tế chúng ta thường sử dụng các biến đổi Z hữu tỷ và ta có thể viết biến đổi Z dưới dạng sau đây:



X zN z 

D z

(2.29)

Phương pháp này chính là việc tiến hành khai triển biến đổi Z này thành các phân thức tối giản sau đó tìm biến đổi Z ngược của các phân thức này, kết quả cuối cùng là tổng các biến đổi Z ngược của các phân thức tối giản này.

Giả sử N(z) là đa thức bậc M, D(z) là đa thức bậc N

Nếu hàm X(z) có bậc của đa thức ở mẫu D(z) lớn hơn bậc của đa thức ở tử N(z), tức là N > M thì nó được gọi là hàm X(z) dạng chính tắc. Trong trường hợp hàm X(z) có N M thì nó là hàm dạng không chính tắc. Khi đó, bằng cách chia đa thức ở tử cho đa thức ở mẫu hoặc bằng biến đổi toán học, sẽ nhận được hàm X(z) dạng:



X (z) S zP z S zX , (z)

Q z

(2.30)

Trong đó X’(z) là hàm dạng chính tắc. Vì S(z) là đa thức lũy thừa của Z, nên có thể dễ dàng tìm được biến đổi Z ngược của nó:

M N

s(n) IZT[S (z)] sr(n r)

r 0

(2.31)

Vì vậy, trong mọi trường hợp chỉ cần nghiên cứu phương pháp tìm biến đổi Z ngược của hàm X(z) dạng chính tắc. Có thể biểu diễn hàm X(z) chính tắc qua các cực điểm zpk:

N (z)

(b zMb z1b z2 ... b

).z( N M )

X (z) 0 1 2 M

D(z) (z zp1)(z zp2 )....(z zpN )

(2.32)

Các cực điểm zpk của hàm X(z) có thể là các cực đơn (cực có giá trị khác nhau), hoặc các cực bội bậc q (q cực có giá trị giống nhau), hơn nữa zpk có thể là các số thực hoặc số phức. Trước hết chúng ta nghiên cứu trường hợp X(z) có nghiệm đơn giản.

- Trường hợp hàm X(z) chỉ có các cực đơn là số thực

Khi X(z) dạng chính tắc và có N cực đơn zpk là số thực (N cực thực đơn), thì có thể phân tích X(z) thành tổng của các phân thức đơn giản dạng:



B(z) N A

X (z) A

D(z)

k

k 1 (z zpk )

A A A

(2.33)

12 ... N

(z zp1 ) (z zp2 ) (z zpN )

Để xác định hệ số Ak , nhân cả hai vế của (2.33) với (z - zpk ) :

X (z)(z z

) A1 (z zpk ) A2 (z zpk )  ... A

 ... AN(z zpk )

pk (z z

p1) (z zp 2 )

k (z z )

Tại z= zpk thì trừ Ak , còn tất cả các số hạng khác ở vế phải của biểu thức trên đều bằng không, do đó có:

AkX (z)(z zpk )

zzpk

(2.34)

Lấy biến đổi Z ngược hàm X(z), tìm được dãy x(n) :

N A N

1 z 

x(n) IZT X (z)IZT kAk IZT z 

Ta thu được dãy x(n) như sau:

k 1 (z zpk) 

k 1

 (z zpk ) 

x(n) B z(n1)u(n 1),

RC X z : z  max z 

(2.35)

k pk

k 1



pk 

Dãy (2.35) có dạng trễ, để nhận được các dãy x(n) không ở dạng trễ như trên, chia cả hai vế cho z và phân tích hàm :

X (z) N (z) N A

k

z zD(z) k 0 (z zpk )

Chỉ số k chạy từ 0, do z.D(z) = 0 có thêm một nghiệm zp0 = 0 (hoặc B(z) = 0 giảm một nghiệm tại z01 = 0 ). Ta được :

N z

k 0

X (z) Ak (z z )

Trong đó, các hệ số Ak được xác định theo biểu thức:

A X (z) (z z )

(2.36)

k z pk 

zzpk

Lấy biến đổi Z ngược hàm X(z), ta tìm được dãy x(n) :

N z 

k 0



x(n) IZT X z IZT Ak(z z ) 

với:

RC Xz:z

 max zpk , nhận được:

x(n) IZT X (z)A z u(n)

k pk

(2.37)

Ví dụ 4:

Cho:

X (z) 

(z  5) (2z2  8z  6)

k 0

Hãy tìm x(n) bằng phương pháp khai triển thành phân thức tối giản.

Giải:

Hàm X(z) là phân thức dạng chính tắc. Vì đa thức đặc trưng có

a0  2  1 nên

phải nhóm thừa số 2 ra ngoài. Để nhận được hàm gốc x(n) dạng không trễ, phân tích hàm:

X (z) 

(z  5) 

(z  5)

A0 

A1 A2

z 2z(z2  4z  3) 2z(z 1)(z  3) z (z 1) (z  3)

Theo (2.36), xác định được các hệ số

A0 ,

A1 , và

A2 :



A 

(z  5)z 

A 5 5

0  2z(z 1(z  3) 

z 0

0 2(1)(3) 6



A 

(z  5)(z 1) 

A 

(1 5)

6 3

1  2z(z 1)(z  3) 

z 1

1 2.1(1 3)

4 2



A 

(z  5)(z  3) 

A 

(3  5)

 8  2

2  2z(z 1)(z  3) 

z 3

2 2.3.(3 1) 12 3

Vậy:

X (z)  5 1  3 1  2 1

z 6 z 2 (z 1) 3 (z  3)

Suy ra:

X (z) 5 3 z 2 z

6 2 (z 1) 3 (z  3)

Vì dãy x(n) là nhân quả nên RC X z  : z

 3 nên :

x(n) IZT X (z)5 (n) 3 u(n) 2 3n u(n)

6 2 3

- Trường hợp hàm X(z) có nhiều cực dạng phức tạp