Biểu Diễn Tín Hiệu Và Hệ Thống Rời Rạc Trong Miền Z

1 

n

h1 n2

0 n 2

0 c¸c gi¸ trÞ cßn l¹i

h n1n1u n2u n6

22

h nrect n

3 11

Tìm đáp ứng xung h(n) của hệ thống tổng quát.

Có thể bạn quan tâm!

• Phương Pháp Giải Phương Trình Sai Phân Tuyến Tính Hệ Số Hằng
• Sơ Đồ Thực Hiện Hệ Thống Đệ Quy Và Không Đệ Quy
• Xử lý tín hiệu số - 7
• Xử lý tín hiệu số - 9
• Các Phương Pháp Biến Đổi Z Ngược
• Định Lý Giá Trị Đầu Của Dãy Nhân Quả

Xem toàn bộ 272 trang tài liệu này.

Bài 1.21

Cho một hệ thống tuyến tính bất biến được mô tả bằng phương trình sai phân sau đây:

ynb0xnb1xn1b2xn 2b4xn 4

Vẽ sơ đồ thực hiện hệ thống.

Bài 1.22

Cho các hệ thống tuyến tính bất biến được ghép với nhau theo sơ đồ hình BT 1.22: Với h1(n) = h2(n) = u(n) - u(n-4)

a. Tìm đáp ứng xung h(n) của hệ thống tổng quát.

b. Nhận xét tính ổn định và tính nhân quả của hệ thống tổng quát.

h1(n)

h2(n)

x(n) y(n)

Hình BT 1.22

Bài 1.23

Hãy tìm đáp ứng xung của hệ thống tuyến tính bất biến có đáp ứng ra là:



1

1m 

y n x n 

x n 1  ... x n m

 ...

3  3 

Nhận xét tính nhân quả và ổn định của hệ thống.

Bài 1.24

Cho hệ thống có kích thích

x(n) u(n)

và đáp ứng xung

h n1

2

n



u n.

Xác định đáp ứng của hệ thống.

Bài 1.25

Cho tín hiệu vào

x nunun 10và hệ thống có đáp ứng xung là:

2

n

h n1



u n

Xác định đáp ứng của hệ thống.

Bài 1.26

Cho hệ thống có đáp ứng xung

h n1

2

n



u n

với tín hiệu vào:

x n2nun

Xác định đáp ứng của hệ thống.

Bài 1.27

Cho hệ thống với đáp ứng xung

1 n



h n2 



0

0 n 4

n cßn l¹i

Xác định kích thích x(n) với 0 n  8

dạng dãy số như sau:

để tạo ra đáp ứng được biểu diễn dưới



Bài 1.28

y n1,2,2,5,3,3,3,2,1,0,...



Tìm đáp ứng xung h(n) của hệ thống được cho bởi sơ đồ cho trên hình BT 1.28 sau đây:

xn

D

0,5

D

yn

Hình BT 1.28

Bài 129

Cho hệ thống được mô tả bởi sơ đồ sau:

xn

yn

D 1 6 D

D

1

8

D

Biết

Bài 1.30

y(n)  0

với

Hình BT 1-29

n 0. Tìm đáp ứng đầu ra y(n)

x(n)  3n u(n)

với kích thích đầu vào là :

Cho hệ thống rời rạc được thực hiện bởi cấu trúc trên hình BT 1.30

x(n)

+

+

0.8

3

y(n)

Z-1

2

Hình BT 1.30 Xác định đáp ứng xung của hệ thống.

Bài 1.31

Cho hệ thống thời gian rời rạc có cấu trúc như trong hình BT 1.31. Biết y(n)=0 với n < 0

x(n)

+

+

y(n)

0.9

2

+

3

Z-1

Z-1

Hình BT 1.31

Tính 3 đáp ứng xung đơn vị của hệ thống với n = 0, n = 1 và n = 2.

Bài 1.32

Cho

xnrect3 n

Xác định hàm tự tương quan

rxx n.

CHƯƠNG 2: BIỂU DIỄN TÍN HIỆU VÀ HỆ THỐNG RỜI RẠC TRONG MIỀN Z

Phép biến đổi là một công cụ quan trọng trong việc phân tích tín hiệu và các hệ thống tuyến tính bất biến theo thời gian. Trong chương 2, chúng ta sẽ dùng biến đổi Z để biểu diễn tín hiệu và hệ thống trong miền Z. Phương pháp khảo sát gián tiếp trong miền Z đặc biệt quan trọng trong việc phân tích tín hiệu và hệ thống rời rạc vì nó cho những kết quả khả quan mà nếu khảo sát trực tiếp trong miền tự nhiên n sẽ rất phức tạp. Biến đổi Z đóng vai trò như biến đổi Laplace trong việc phân tích tín hiệu và hệ thống tương tự.

Quan hệ giữa miền n và miền Z được mô tả trên hình 2.1.

ZT

Miền n

Miền Z

IZT

Hình 2. 1.Quan hệ giữa miền n và miền Z ZT: Z Transform (biến đổi Z)

IZT: Inverse Z Transform (biến đổi Z ngược)

2.1. Biến đổi Z

2.2.1. Biến đổi Z hai phía và một phía

a. Biến đổi Z hai phía

Định nghĩa: Biến đổi Z hai phía của một dãy x(n) được định nghĩa như sau:



X (z) x(n). zn n

(2.1)

Ký hiệu bởi toán tử:

ZT[x(n)] X (z)

(2.2)

Hay:

x(n) ZTX (z)

(ZT là chữ viết tắt của thuật ngữ tiếng Anh: Z - Transform).

Đối với biến đổi Z hai phía, ta có thể gọi tắt là biến đổi Z. Ở đây, z là một biến số phức.

Ví dụ 1:

Hãy xác định biến đổi Z hai phía của các dãy sau:

a. (n)

b. n k 

c. (n  )

d. x(n) 

e. u(n)

Giải :

f. u(n 3)



k

g. u(n 3)

h. u(n)

3, 2, 5,1



a. ZT[(n)] (n). zn  1

n

Chuỗi hội tụ với mọi z, nên ZT[(n)] xác định với mọi z.



b. ZT[(n k )] (n k). zn zk n

Chuỗi hội tụ với mọi z > 0, nên ZT[(n k)] xác định với mọi z > 0.



c. ZT[(n k )] (n k). zn zk n

Chuỗi hội tụ với mọi z < , nên ZT[(n k)] xác định với mọi z < .

 2

d. X (z) 

x(n)zn x(n)zn

 3z1  2  5z1 z2

nn1

Hàm X(z) xác định trong miền 0 < z < .



e. ZT[u(n)] 

u(n)zn 

zn  1z



n

n0

(1z1 ) z 1

Dãy nhân quả vô hạn u(n) có biến đổi Z bằng  tại z = 1

f. ZT[u(n  3)] 





n



u(n  3)zn 

n3



zn 

m0

z(m3) z3z

(z 1)

1

z2 (z 1)

Ta đã đổi biến, đặt (n  3) m

n  (m  3) và khi

n 3

thì

m  0

Dãy nhân quả vô hạn u(n  3) có biến đổi Z bằng  tại z = 1 và z = 0



n n



(m3) 3

z z4

g. ZT[u(n  3)] u(n  3)z

n

z

n3

z

m0

z (z 1) 

(z 1)

Ta đã đổi biến, đặt (n  3) m 

n  (m  3) và khi n  3 thì

m 0





Dãy không nhân quả u(n  3) có biến đổi Z bằng  tại z = 1 và z = 



h. ZT[u(n)] 

u(n).zn 

u(n).zn 

u(m).zm 

zm  1

0

n

n

m0

m0 (1 z)

Ta đã đổi biến, đặt

n m

 khi n  thì m 

Dãy phản nhân quả vô hạn u(n) có biến đổi Z bằng  tại z = 1

Ví dụ 2:

Tìm ZT của các tín hiệu có chiều dài vô hạn sau đây:

Giải:

0,5n

e

x5 n

0

e

0,5n

x6 n

0

n 2

n 2

n  0

n  0

n

X z x

zZ n 

e0,5n zn ez2 e0,5 ze0,5 z1 

5 5

n

n

n0

= ez2 e0,5z 1

1 e0,5z1

với

z e0,5 , z 

n

X z x

zZ n 

e0,5n zn e0,5 z1 

6 6

n

n

n0

1 víi 1 e0,5z1

b. Biến đổi Z một phía Định nghĩa:

z e0.5

Biến đổi Z một phía của dãy x(n) là chuỗi lũy thừa của biến số phức z:



X 1 (z) 

n0

x(n). zn

(2.3)

Miền xác định của hàm Ký hiệu bởi toán tử:

X 1 (z) là các giá trị của z để chuỗi hội tụ.

Hay :

ZT1[x(n)] X 1(z)

1 1

x(n) ZTX (z)

(2.4)

Sự khác nhau giữa biến đổi Z một phía và hai phía:

- Tổng theo n chỉ chạy từ 0 

- Không biểu diễn được tín hiệu x(n) đối với miền biến số độc lập âm (n < 0)

- Biến đổi Z một phía và hai phía với tín hiệu nhân quả là như nhau.

- Đối với tín hiệu nhân quả thì biến đổi Z một phía là duy nhất, vì tín hiệu nhân quả bằng 0 với n < 0.

- Về ký hiệu, để phân biệt với biến đổi Z hai phía, ta ghi số 1 ở phía trên bên

trái:

X 1 (z) ,

ZT1 số 1 có nghĩa là một phía.

Ví dụ 3:

Hãy xác định biến đổi Z một phía của các dãy ở ví dụ 1 và so sánh kết quả với biến đổi Z hai phía tương ứng.

a. (n)

b. (n k)

c. (n k)



d. x(n)  {3, 2, 5,1}

e. u(n)

Giải:

f. u(n 3)



g. u(n 3)

h. u(n)

a. ZT1[(n)] (n). zn  1

n0

Dãy nhân quả (n) có biến đổi Z một phía giống biến đổi Z hai phía.



b. ZT1[(n k)] (n k) zn zk

n0

Dãy nhân quả (n k) có biến đổi Z một phía giống biến đổi Z hai phía.



c. ZT1[(n k)] (n k)zn 0zn  0

n0 n0

Dãy phản nhân quả (n k) có biến đổi Z một phía luôn bằng 0.

 2

d. X 1 (z) x(n)zn x(n)zn  2  5z1 z2

n0 n0

Dãy không nhân quả x(n) có biến đổi Z một phía khác biến đổi Z hai phía



e. ZT1[u(n)] 

u(n)zn 

zn  1z



n0

n0

1z1 z 1

Dãy nhân quả u(n) có biến đổi Z một phía giống biến đổi Z hai phía.



f. ZT1[u(n  3)] 

n0



u(n  3)zn 

n3



zn 

m0

zm3 z3z

z 1

1

z2 (z 1)

Dãy nhân quả u(n 3) có biến đổi Z một phía giống biến đổi Z hai phía.



g. ZT1[u(n  3)] 

n0



u(n  3)zn 

n0

zn z

z 1

Dãy không nhân quả u(n  3) có biến đổi Z một phía khác hai phía.



h. ZT1[u(n)] u(n)zn 0zn 0

n0 n0

Dãy phản nhân quả vô hạn u(n) có biến đổi Z một phía luôn bằng 0.

Như vậy, các dãy nhân quả có biến đổi Z một phía và hai phía giống nhau, các dãy không nhân quả có biến đổi Z một phía và hai phía khác nhau, các dãy phản nhân quả có biến đổi Z một phía bằng không.

Ví dụ 4:

Tìm biến đổi Z một phía của các tín hiệu có chiều dài vô hạn sau đây:

e

0,5n

x5 n

0

n 2

n 2

Giải:

0,5n

e

x6 n

0



n  0

n  0

5 5

X 1 zx

n0

zZn e0,5n zn n0

1 víi 1 e0,5z1

z e0.5

n

6 6

X 1 zx

zZ n 

e0,5n zn e0,5 z1 

n0

n

n0

1 víi 1 e0,5z1

c. Mặt phẳng Z

z e0.5

Ở đây, z là một biến số phức và được biểu diễn theo hai dạng:

+ Biểu diễn theo phần thực, phần ảo: Re[z], Im[z]:

z = Re[z] + j.Im[z] (2.5)

Imz

Mặt phẳng z

0

Rez

Hình 2. 2. Biểu diễn theo phần thực, phần ảo

+ Biều diễn theo tọa độ cực:

z re jr cosj sinr cosj sin

RezImz

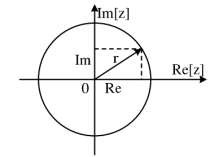
Hình 2. 3. Biểu diễn theo tọa độ cực

(2.6)

- Trường hợp đặc biệt:

z r  1 ta có vòng tròn đơn vị.