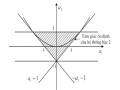
Vẽ h nvới c2 ,c1 và N = 7
2 3
sin n 3
sin n 3
h(n) 1
2
2
n 3
1
3
3
n 3
2 3
h(3) 1 1 1
2 3 6
3
h(2) h(4) 1
3
2
h(1) h(5)
4
h(0) h(6) 1
3
3
h(1) h(7)
8
Bài 4.4
h(n) 1
4
h(n)
1
6
1 3
1 3 3
2
28
-4 -3 -2 -1 0
1
2
3
4 5 6 7
3
8
n
1
3
3
H e je jn d
2
1 jN 1
1 c 2
jN 1
1 c1
jN 1
2
e
2 e jn d
e
2
c 2
2e jnd
e
2
c1
2ejnd
sin
n N 1
sin
n N 1
N 1
c 2
2
c1
2
(n
) [c 2 c1 ]
2 n N 1n N 1
c 2 2 c1 2
sin n 3sin n 3
h(n) (n 3) [ 1
2
2
n 3
1
3
3
n 3
]
2 3
h(3) 1 ( 1 1) 5
2 3 6
h(2) h(4) 1 3
3
2
h(1) h(5)
4
h(0) h(6) 1
3
3
h(1) h(7)
8
h(n)
5
6
3
4
1
3
-4 -3 -2 -1 0 1 2 3 4 5 6 7 3n
1 3 8
Bài 4.5
2
Vì 0 và N lẻ nên đây là bộ lọc số FIR pha tuyến tính loại 1
Ta có :
N 1 5 1 2
2 2
Ta có: h(n) = h(5-1-n) = h(4-n)
Vậy : h(4) = h(0) = -1;
h(3) = h(1) = 1; h(2) = 2
Vẽ đáp ứng xung:
2
1
0
1 2
3 4 n
-1
h(n)
Bài 4.6
Vì
0 và N chẵn nên đây là bộ lọc FIR pha tuyến tính loại 2.
Ta có :
N 1 4 1 1,5
2 2
Ta có: h(n) = h(4-1-n) = h(3-n)
Vậy: h(3) = h(0) = -1 h(2) = h(1) = 1
Vẽ đáp ứng xung:
h(n)
1
0
1
2 3
-1
n
Bài 4.7
Vì
0 và N lẻ nên đây là bộ lọc FIR pha tuyến tính loại 3
Ta có :
N 1 7 1 3
2 2
Ta có: h(n) = -h(7-1-n) = -h(6-n)
Vậy : h(6) = -h(0) = 1
h(5) = -h(1) = 0,5
h(4) = -h(2) = 1,5 h(3) = 0
Vẽ đáp ứng xung:
1,5
1,0
0,5
0
-0,5
-1,0
-1,5
2 3 4
5
6 n
1
h(n)
Bài 4.8
Vì
0 và N chẵn nên đây là bộ lọc FIR pha tuyến tính loại 4
Ta có :
N 1 4 1 1,5
2 2
Ta có: h(n) = -h(4-1-n) = -h(3-n)
Vậy : h(3) = -h(0) = 1
Vẽ đáp ứng xung:
h(2) = -h(1) = -1
h(n)
1
0 1 2 3 n
-1
Bài 4.9
Đáp ứng pha :
N 1 5 1 2 () 2
2 2
2
Đáp ứng biên độ tần số :
H (e j) a(n) cos(n)
n0
a(0) h N 1h(2) 2
2
a(1)
N 1
2h(1) 2
2h1
2
Vậy:
Bài 4.10
a(2) 2h(2 2) 2h(0) 2
H (e j) 2 2cos() 2cos(2)
1
0
1
2 3
n
-1
h(n)
Đáp ứng pha :
N 1 4 1 1,5 () 1,5
Đáp ứng biên độ tần số :
2
2
H (e j)
2
2
b(n) cosn 1
n1
b(1)
2 N
h2
2h(2 1) 2h(1) 2
1
Vậy:
b(2) 2h(2 2) 2h(0) 2
H (e j) 2cos(0,5) 2cos(1,5)
Bài 4.11
Đáp ứng pha :
N 17 11,5 () 3
2 2 2
Đáp ứng biên độ tần số :
Vậy:
Bài 4.12
2
H(ej) c(n).sin(.)
n1
c(1) 2.h(1) 2.h(3 1) 2.h(2) 2.1,5 3
c(2) 2.h(1) 2.0,5 1
c(3) 2.h(0) 2.1 2
H(ej) 3.sin() sin(2) 2.sin(3)
Đáp ứng pha :
N 14 11, 5 ()
1, 5
2 2 2
j2 1
Đáp ứng biên độ tần số :
H(e
) d(n).sin .(n )
n1
2
Vậy:
Bài 4.13
d(1) 2.h( N 1) 2.h(1) 2 ;
2
d(2) 2.h(2 2) 2.h(0) 2
H(ej) 2sin(0,5) 2sin(1,5)
Ta có phổ của hàm cửa sổ chữ nhật:
j
wR (e )N FT[wR (n)N ]
= w
n
R (n)N
N1
ejn ejn
n0
N
1 ejN
= 1 ej
sin
2
sin
2
jN 1
e2
Từ đó ta vẽ được đồ thị hàm biên độ tần số như sau :
wR (e )N
j
N
0
246
2
N N N
Bài 4.14
Ta có:
wT (n)N
2 rect
N 1
N 1
(n)* rect
N 1
(n 1)
2 2
= 2
N 1
wT (n)N1* w
T (n 1)N 1
2 2
Từ đó suy ra phổ của hàm cửa sổ tam giác:
T N
w (ej)
2 w
R N1
N 1
(ej) .ejw
(e )
j
R N1
N 1
sin 2
j2
2 2
N 11
j2
Mà:
Vậy:
wR (e
)N 1
2
e 2
sin
2
w (e j)
T N
2 .e
N 11
j2
2 .
N 1 sin 2
2
.ej.e
N 11
j2
2 .
N 1 sin 2
2
N 1 sin sin
2 2
2
N 1
2
sin
2
jN 1 2
Bài 4.15
N 1 e
2
sin
2
Do chiều dài của
wH (n)N
là N nên ta có thể viết:
wH (n)N
(1)cos
2
N 1
nw
R (n)N
Biến đổi tiếp ta được:
2
w (n) w (n) (1 )w (n) cos n
H N R N R N
N 1
j n
22
w
R (n)N
1 (1)w 2
R (n)N
e N1 1 (1)w 2
R (n)N
j n
eN1
Lấy biến đổi Fourier 2 vế ta được:
1
j2n 1
j2n
FT w
(n)
FT w
(n)
(1)FT w
(n)
e N1
(1)FT w
(n) e
N1
H N R N2
R N 2 R N
22
w (ej)
w
(ej)
1 (1)w
j ()
(e N1 )
1 (1)w
j ()
(e N1 )
H N R N 2 R N 2 R N
N
sin
jN1
R N
Mà :
w (e j)
2 e 2
sin
j (2) N1
2
jN1
jN1
Và :
e N1 2 e
2 .e j
e 2
Vậy :
j (2) N1
e N1 2
jN1
e 2
.ej
jN1
e 2
sin Nsin N
sin N
jN1
1
2 N 1
1
2 N 1
w (ej) e 2 2
H N
2 2
sin
2
sin 2 N 1
sin 2 N 1
Cửa sổ Hanning:
0, 5
sin
NN
0, 5 sin
sin N
jN1
2 N 1
2 N 1
w (e j) e 2
2 0, 25
0, 25
H N
sin
2
sin 2 N 1 sin 2 N 1
Bài 4.16
Tương tự như bài 4.11: Cửa sổ Hamming:
0, 54
sin
NN
0, 54 sin
sin N
jN1
2 N 1
2 N 1
w (e j) e 2
2 0, 23
0, 23
H N
sin
2
sin 2 N 1 sin 2 N 1
Bài 4.17
Tương tự bài 4.12, ta vẽ được hàm biên độ tần số của cửa sổ tam giác như hình
sau:
wR (e )N
j
N
2
0
N
2
N
Từ đó ta tính được bề rộng đỉnh trung tâm :
Bài 4.18
4
N
Tương tự bài 4.13, ta vẽ được hàm biên độ tần số của cửa sổ tam giác như hình sau:
wR (e )N
j
N
S
0
S
Tỷ số giữa biên độ đỉnh thứ cấp thứ nhất trên biên độ đỉnh trung tâm được tính như sau:
w(ejs)
w(ej0)
20 lg 13dB
Bài 4.19
Theo đầu bài ta chọn cửa sổ chữ nhật WR (n)N
là cửa sổ nhân quả tâm đối xứng
tại
N 1
2
với N=5
Bộ lọc số lý tưởng thông thấp có dạng:
h(n) c sin c n
c n
sin (n N 1
c )
h(n) c 2
(n N 1)
c2
Với
và N=5
1 sin[ 6 (n 2)]
c h(n)
6 6
(n 2) 6
Nhân cửa sổ WR (n)5 với h(n) lý tưởng ta được:
hd (n) WR (n)5.h(n)
Kết quả phép nhân thể hiện trên bảng sau:
0 | 1 | 2 | 3 | 4 | |
h(n) | 3 4 | 1 2 | 1 6 | 1 2 | 3 4 |
WR (n) | 1 | 1 | 1 | 1 | 1 |
hd (n) | 3 4 | 1 2 | 1 6 | 1 2 | 3 4 |
Có thể bạn quan tâm!
Xem toàn bộ 272 trang tài liệu này.