Khoảng Tin Cậy Cho Độ Lệch Hai Giá Trị Tỷ Lệ.

n1 ;n2 30	n 30; X ~ N  ; 21 1 1 1 n 30; X ~ N  ; 22 2 2 2
Biết  2 ; 2 1 2	 2  2  z /2 1 2 n1 n2	 2  2  z /2 1 2 n1 n2
Chưa biết  2	 S 2 S2 z /2 1 2 n1 n2	 n n 2 S 2 S 2 t 1 2  /2 n n 1 2

Có thể bạn quan tâm!

• So Sánh Trung Bình (Mean), Trung Vị (Median), Yếu Vị (Mod)
• Các Khuynh Hướng Đo Vị Trí Tương Đối.
• Khoảng Tin Cậy Cho Độ Lệch Hai Giá Trị Trung Bình 81
• Kiểm Định Giả Thiết Cho Một Giá Trị Tỷ Lệ Tổng Thể.
• Kiểm Định Giả Thiết Cho Hai Giá Trị Tỷ Lệ Tổng Thể.
• Kiểm Định Giả Thiết Cho Hai Phương Sai Tổng Thể

Xem toàn bộ 142 trang tài liệu này.

S S

2 2

n1 n2



X1X2 ; X1X2 

Trong đó độ chính xác được tính theo công thức

Trong đó khi cỡ mẫu của hai mẫu đều nhỏ thì phương sai mẫu của kết hợp hai mẫu là

S 2 



n 1 S n 1 S

1



2

1 2



2

2

n1 n2 2

z /2



2

1



2

 

n1 n2

2; z /2 được tính theo phân phối chuẩn.

 t

n n 2

1 2

 /2

; t

1 2

 /2

n n 2

được tính theo phân phối Student.

Trường hợp 2: Hai mẫu dữ liệu lấy phối hợp từng cặp. (Hai mẫu dữ liệu phụ thuộc).

Giả sử ta có mẫu n cặp quan sát x, ylấy từ hai tổng thể X ,Y :x1,y1;x2,y 2;...,xn,yn, gọi

1, 2là trung bình của hai tổng thể. Ta lặp bộ dữ liệu mới là sự chênh lệch của từng cặp giá trị,

và d , d lần lượt là trung bình và độ lệch chuẩn của bộ dữ liệu mới. Với độ tin cậy 1 

ước lượng cho sự chênh lệch hai giá trị trung bình của hai tổng thể là khoảng

d  ;d  

Trong đó độ chính xác tính theo các trường hợp sau

thì khoảng

n 30	n 30
d đã biết 2	 z  d  /2 n	 z  d  /2 n
d chưa biết 2	 z Sd  /2 n	 t n1 . Sd  /2 n

n

n



 z

 d

 /2

; z

 /2

được tính theo phân phối chuẩn.



 t n1 . Sd ; t n1 được tính theo phân phối Student.

 /2

 /2

Ví dụ 5.4 Công ty điện lực thực hiện các biện pháp khuyến khích tiết kiệm điện. Lượng điện tiêu thụ ghi nhân ở 12 hộ gia đình trước và sau khi có các biện pháp khuyến khích tiết kiệm điện như sau

Hộ gia

đình

Lượng điện tiêu thụ (kwh) Hộ gia Lượng điện tiêu thụ (kwh)
Trước Sau	đình	Trước	Sau
1	73 69	7	74	75
2	50 54	8	87	78

3

83	82	9	69	64
4	78	67	10	72	72
5	56	60	11	77	70
6	74	73	12	75	63

n

n

Ví dụ 5.5 Một công ty đang xem xét kế hoạch tiết giảm chi phí sản xuất thông qua việc xây dựng dây chuyền sản xuất mới nhằm rút ngắn thời gian sản xuất sản phẩm. Ở dây chuyền sản xuất mới, 40 sản phẩm được sản xuất với thời gian trung bình 46,5 phút, và độ lệch chuẩn 8 phút. Còn dây chuyền cũ 38 sản phẩm với thời gian trung bình là 51,2 phút, và độ lệch chuẩn 9,5 phút. Với độ tin

cậy 95% thì sự chênh lệch về thời gian trung bình sản xuất 1 sản phẩm nằm trong khoảng

X1 X2 z /2 .

  X X z .

1 2 1 2  /2





Trong đó 

X146,5; S18 ;n140

X251,2; S29,5;n238

và 1  95% z/2 1,96

Vậy khoảng ước lượng là 8,6077 1 2 0,7923

Sự thay đổi trung bình về lượng điện tiêu thụ trước và sau khi có các biện pháp tiết kiệm với độ

tin cậy 95% nằm trong khoảng:

d t n1 . Sd  d t n1 . Sd

 /2

1 2

 /2

Trong đó d 3,4167;S 5,4848;n 12;1 95% tn1 2,201

d

 /2

Khoảng ước lượng là 0,0682 126,9016

12

S 2 S 2

n1 n2

12

S 2 S 2

n1 n2

5.4. Khoảng tin cậy cho giá trị tỷ lệ.

5.5.1 Phân tích.

Gọi p là giá trị tỷ lệ phần tử loại A trong một tổng thể. Từ giá trị quan sát X1, X2,..., Xnđộc lập có cùng phân phối nhị thức (trong đó Xi1 cho việc ở lần kiểm tra thứ ݅ ta được phần tử loại ܣ và Xi0 khi không được phần tử loại ܣ), ta cần lập khoảng ước lượng cho p với độ tin cậy 1  .

Xét hàm ước lượng Tn

f X1 X2 ... Xn , ta xây dựng khoảng ước lượng sao cho

n

P f  p f  1 

Định lý. Cho X1, X2,..., Xnlà biến ngẫu nhiên có quy luật phân phối nhị thức, thì Tnf theo quy

luật phân phối chuẩn T f ~ N p; pq 

n

n 





 f p  

Ta có P f  p f  1 

P 1 

pq pq pq 

n n n 

pq

n



Mà T f ~ N p; pqf p ~ N 0;1nên

 z

 z

pq n

n n 

 /2

 /2



pq n

Nhưng trong công thức độ chính xác thì p,q là các tham số tổng thể nên ta sẽ thay bằng tham số mẫu, ta có:

f 1 f n

5.5.2 Quy tắc thực hành.

 z /2

Khoảng ước lượng cho giá trị tỷ lệ p là khoảng f  ; f  .

Trong đó  z

 /2

f 1 f , với z

n

 /2

là phân vị của phân phối chuẩn.

Ví dụ 5.6 Một nghiên cứu được thực hiện nhằm ước lượng thị phần của sản phẩm nội địa đối với mặt hàng bánh kẹo. Kết quả điều tra 100 khách hàng cho thấy có 34 người dùng sản phẩm nội

địa. Với độ tin cậy 95%, ta có khoảng ước lượng cho tỷ lệ khách hàng dùng bánh kẹo nội địa là

f z/2 .

p f z/2 .

Trong đó f 34 ;n 100;1  95% z

100

 /2

1, 96

Vậy khoảng ước lượng là 24,72%p 43,28%

f 1 f n

f 1 f n

Ví dụ 5.7 Trung tâm Quốc gia về Thống kê Giáo dục báo cáo rằng 47% sinh viên cao đẳng làm việc để trả học phí và chi phí sinh hoạt. Giả sử một mẫu của 450 sinh viên cao đẳng được sử dụng trong nghiên cứu.

a. Cung cấp một khoảng tin cậy 95% cho tỷ lệ tổng thể sinh viên cao đẳng làm việc để trả cho học phí và chi phí sinh hoạt.

b. Cung cấp một khoảng tin cậy 99% cho tỷ lệ tổng thể sinh viên cao đẳng làm việc để trả học phí và chi phí sinh hoạt.

c. Điều gì xảy ra với sai số biên khi độ tin cậy gia tăng từ 95% đến 99%?

Giải.

a. Cung cấp một khoảng tin cậy 95% cho tỷ lệ tổng thể sinh viên cao đẳng làm việc để trả cho học phí và chi phí sinh hoạt.

Ta có:

f 1f n

0, 47 1 0, 47

450

f  47%, n  450 , z / 2  1, 96

 z /2

 1,96 0, 0461

f; f  0, 47  0, 0461;0, 47  0, 04610, 4239;0, 5161

b. Cung cấp một khoảng tin cậy 99% cho tỷ lệ tổng thể sinh viên cao đẳng làm việc để trả học phí và chi phí sinh hoạt.

f  47%, n  450 , z / 2  2, 58

 z /2

f 1f n

 2,58

0, 47 1 0, 47 0, 0607

450

f  ; f  0, 47  0, 0607; 0, 47  0, 06070, 4093;0,5307

c. Điều gì xảy ra với sai số biên khi độ tin cậy gia tăng từ 95% đến 99%?

Sai số biên với độ tin cậy 95%, bằng 0,0461, nhỏ hơn sai số biến với độ tin cậy 99%, bằng 0,0607, là 0,0146.

5.5. Khoảng tin cậy cho độ lệch hai giá trị tỷ lệ.

5.5.1 Phân tích.

Gọi p1 , p2 lần lượt là tỷ lệ của phần tử loại A trong 2 tổng thể. Khoảng ước lượng cho độ lệch hai

tỷ lệ đối với độ tin cậy 1 

thông qua hàm ước lượng Z f1 f2 (với

f1 , f2 lần lượt là tỷ lệ phần

tử loại A trên 2 mẫu độc lập của hai tổng thể) thỏa

P f1f2 p1p2f1f2 1

5.5.2 Quy tắc thực hành

Khoảng ước lượng cho độ lệch giữa hai giá trị tỷ lệ p1p2là khoảng:

f1 f2  ; f1 f2  

Trong đó giá trị độ chính xác cho bởi:

 z .

 /2

f1 1 f1 f2 1 f2 

n

1

n

2

Được tính thông qua z/2 là phân vị của phân phối chuẩn.

Ví dụ 5.8 Kết quả điều tra từ mẫu ngẫu nhiên 1000 người ở mỗi thành phố cho thấy năm 2014

tỷ lệ thất nghiệp ở thành phố Hồ Chí Minh là 7,5%, ở thành phố Phan Thiết là 7,2%; với độ tin cậy 99% thì sự chệnh lệch về tỷ lệ thất nghiệp của 2 thành phố nằm trong khoảng

f1f2z/2 .

p1p2f1f2z/2 .

Trong đó

p10,075;n11000 và1  99% t

p 0,072;n 1000

2

 /2

2,575

2

Vậy khoảng ước lượng là 0,027 p1 p2 0,033

Vì vùng giá trị nằm đều xung quanh 0 nên ta không thể kết luận thành phố nào có tỷ lệ thất nghiệp

cao hơn, ta chỉ có thể kết luận tỷ lệ thất nghiệp của thành phố Hồ Chí Minh trong khoảng từ thấp

hơn 2,7% đến cao hơn 3,3% so với thành phố Phan Thiết.

f1 1 f1 f2 1 f2 

n1

n2

f1 1 f1 f2 1 f2 

n1

n2

5.6. Khoảng tin cậy cho giá trị phương sai.

i. Phân tích.

1 2 n

Gọi  2là phương sai của tổng thể chưa biết. Từ giá trị quan sát X , X ,..., X độc lập có cùng phân

n

phối chuẩn, ta cần lập khoảng ước lượng cho  2 với độ tin cậy 1  . Xét hàm ước lượng T

S 2

, ta xây dựng khoảng ước lượng sao cho:

P A  2 B1

Định lý. Cho X1, X2,..., Xnlà biến ngẫu nhiên có quy luật phân phối chuẩn với kỳ vọng là  và

phương sai là  2, và S2là phương sai mẫu (có hiệu chỉnh). Thì ta có

n 1S2

2

~2,n1

Là phân phối Chi bình phương với n 1bậc tự do.

 /2 1 /2

Ta có P 2,n1 2,n1  2,n1 1 .



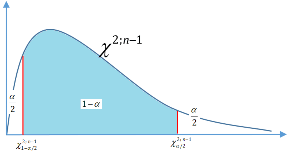
Nên ta có P 2,n1 

n 1S 2



~ 2,n1 2,n1 1 

thay vào phương trình ta có

2

 /2



1 /2



n 1S 2n 1S2

P 



2,n1



1 /2

 2 

 2

2,n1



 /2

1 



n 1S 2

n 1S 2 

Vậy khoảng ước lượng cho

ii. Quy tắc thực hành.

với độ tin cậy 1  là 



2,n1



1 /2

; 2,n1 



 /2 

Khoảng tin cậy cho  với độ tin cậy 1  100% là S  ;S  .Khoảng tin cậy có công

2







2

2

1

2



thức

n 1S 2 n 1S 2 





 2,n1 2,n1

;

1 /2

 /2





Trong đó  2,n1 ;  2,n1 tính theo phân vị Chi bình phương.

 /2 1 /2

S n 1

Đây là khoảng ước lượng hai phía, nghĩa là với giá trị chặn trên và chặn dưới chấp nhận sai số với mức ý nghĩa  / 2.100% . Trong trường hợp ước lượng một phía, nghĩa là chặn trên hoặc chặn dưới sẽ chấp nhận sai số với mức ý nghĩa  100% ta có ước lượng tương ứng:

2

2,n1

Ước lượng phải (chặn trên) với độ tin cậy 1  100% :  2 .



S2 n 1

Ước lượng trái (chặn dưới) với độ tin cậy 1  100%:



2,n1

1

 2 .

Ví dụ 5.9 Khảo sát thời gian tự học (giờ) trong 1 tuần của sinh viên một trường cao đẳng, khảo sát số liệu trên 78 sinh viên ta có bảng số liệu sau

Số giờ

5	6	7	8	9	10
Số sinh viên	2	25	30	15	4	2

Với độ tin cậy 95%, ước lượng cho phương sai thời gian tự học của sinh viên sẽ nằm trong khoảng là

n 1S2



2,n1

1 /2

 2 

n 1S2



2,n1

 /2

Trong đó n 78 ;S 2 1,065 và 1  95% 0 ,025

 2,77 54,62



 104,3

2,77

0 ,975

Vậy khoảng ước lượng cho phương sai là 0,7946  2 1,5014

5.7. Khoảng tin cậy cho dự đoán giá trị quan sát

i. Phân tích

Trong một số trường hợp ta phải dự đoán một giá trị sẽ xảy ra của biến ngẫu nhiên, ta sẽ đưa ra một phương pháp để thu được khoảng dự đoán cho giá trị tương lai theo quy luật phân phối chuẩn.Giả sữ X1, X2,..., Xnlà biến ngẫu nhiên có quy luật phân phối chuẩn. Ta cần dự đoán khoảng giá trị cho biến ngẫu nhiên Xn1 . Điểm dự đoán cho Xn1 là trung bình mẫu X , với sai số dự đoán

là Xn1 X .

Kỳ vọng của sai số dự đoán là E Xn1 X   0

Phương sai của sai số dự đoán là Var X

X  2  2  2 1 1

n1

n n 

Vì giá trị quan sát Xn1 và trung bình mẫu hoàn toàn độc lập nên chuẩn, do đó:



Xn1 X có quy luật phân phối

Z 

Xn1 X 0

~ N 0,1

Thay thế  bằng S ta có

 1 1

n

T 

Xn1 X 0

1 1

n

S

~ T n1

Ước lượng khoảng cho giá trị Xn1 bằng giá trị trung bình X với độ tin cậy 1 100% :



 X X  

P X  Xn1 X  1 P  n1 1 

1 1

n

S



1 1

n

S S 1 1



n



Với T ~ T n1 ta có P tn1 T tn1 1

 /2

Vậy t n1  t n1 S

 /2

1 1

n

.

S 1 1

n

 /2  /2

ii. Quy tắc thực hành.

Khoảng tin cậy cho Xn1 với độ tin cậy 1 100% là X ; X  

Độ chính xác  t n1S 1 1, tính theo phân vị phân phối Student.

 /2

n

Khoảng ước lượng là X t S 1 ; X tn1S 1 .



n1

1

1





 /2

n

 /2

n 

Ví dụ 5.10 Một bài viết trên tạp chí Vật liệu (năm 1989, Vol. II, số 4, tr. 275-281) mô tả các kết quả của bài kiểm tra độ bám dính trên 22 mẫu hợp kim U-700. Bộ mẫu thu được như sau (theo đơn vị megapascals)

1 1

n

1 1

n

19.8 10.1 14.9 7.5 15.4 15.4 15.4 18.5 7.9 12.7 11.9

11.4 11.4 14.1 17.6 16.7 15.8 19.5 8.8 13.6 11.9 11.4

Với độ tin cậy 95%, khoảng ước lượng cho giá trị dự đoán thứ 23 nằm trong khoảng

X tn1 .S

 /2

X X tn1 .S

23

 /2

Trong đó X 13,71; S 3,55;n 22;1  95% t21 2,08

,25

Vậy khoảng ước lượng cho dự đoán giá trị thứ 23 là : 6,16 X2321,26

CHƯƠNG 6

KIỂM ĐỊNH GIẢ THIẾT THỐNG KÊ

Mục lục chương 7

6.1 Khái niệm. 89

6.2 Kiểm định giả thuyết về tỷ lệ tổng thể 91

6.3 Kiểm định giả thuyết về trung bình tổng thể 93

6.4 Kiểm định giả thuyết về phương sai tổng thể 96

6.5 Kiểm định so sánh hai tỷ lệ của hai tổng thể 98

6.6 Kiểm định so sánh hai trung bình của hai tổng thể 102

6.7 Kiểm định giả thiết cho hai phương sai tổng thể 105

6.8 Kiểm định giả thuyết về sự độc lập 106

Trong phần chương 6 chúng ta đã đưa ra phương pháp để ước lượng cho tham số tổng thể dựa trên dữ liệu mẫu dữ liệu, mục đích của chương 7 là đưa ra phương pháp cho việc kiểm tra các kết luận đối với tham số tổng thể dựa trên mẫu dữ liệu.

Ví dụ 6.1 Một trường đại học, khảo sát về vấn đề tỷ lệ có việc làm của sinh viên sau khi học đại học. Nếu trường đại học muốn đưa ra một số liệu về tỷ lệ có việc làm của sinh viên sau khi học, thì đây là bài toán ước lượng. Trường hợp lúc này, trường đại học muốn khẳng định về uy tính và chất lượng của trường ngày càng tăng, thì nhà trường phải khẳng định tỷ lệ sinh viên có việc làm sau khi học có khuynh hướng tăng so với một mức tỷ lệ mà trường đã đạt được trong những năm trước. Thì bài toán lúc này trở thành kiểm định giả thiết thống kê.

Trong bài toán kiểm định về giả thiết thống kê. Một giả thiết được đặt ra, thì mục tiêu chúng ta muốn là thu thập dữ liệu để có thể khẳng định giả thiết đó là sai. Nhưng khi không thể khẳng định giả thiết ban đầu sai, thì điều này đồng nghĩa là ta chưa thu thập đủ dữ liệu, chứ không phải là giả thiết ban đầu đúng.

Mục tiêu bài toán có một sự tương đồng về qui trình được sử dụng tại một phiên tòa xét xử. Khi xét xử một người vì tội trộm cắp, thì tòa án cho rằng bị cáo là vô tội cho đến khi được chứng minh là có tội. Bên nguyên thu thập và trình bày tất cả các bằng chứng sẵn có trong một nỗ lực nhằm phủ nhận giả thuyết “không có tội” để đạt được kết luận người này có tội. Tuy nhiên, nếu bên nguyên thất bại trong việc bác bỏ giả thuyết “không có tội” này, thì điều này không chứng minh được rằng bị cáo là “vô tội” mà chỉ đơn thuần là chưa có đủ bằng chứng để kết luận rằng bị cáo là “có tội”.

6.1. KHÁI NIỆM

6.1.1 Giả thiết H0 và đối thuyết H1 .

Một kiểm định giả thiết thống kê bao gồm:

Xem tất cả 142 trang.