• Và nếu nhóm đối tượng này được khảo sát nhiều lần mà hệ số tương quan vẫn cao như
vậy thì ta có thể kết luận có thể dựa vào cân nặng để dự đoán vòng eo và ngược lại.
• Nhưng cần hiễu rằng hệ số tương quan không phản ảnh mối quan hệ trực tiếp giữa trọng lượng và vòng eo, còn rất nhiền mối quan hệ ảnh hưởng tới điều này nên ta không thể nói rằng trọng lượng là nguyên nhân làm cho vòng eo rộng hay ngược lại, mối quan hệ ở đây ta quan tâm chỉ là tương quan giữa hai đại lượng ngẫu nhiên ta đang xét.
4.5. Hệ số đo hình dạng của quy luật phân phối.
4.2.1 Hệ số Kurtoris (độ nhọn)
Độ nhọn (kurtosis) là đại lượng thống kê mô tả đo mức độ tập trung của phân phối xác suất của biến ngẫu nhiên, cụ thể là mức độ tập trung của các dữ liệu quanh trung tâm của phân phối trong mối quan hệ với hai đuôi.
Độ nhọn (Kurtosis) là một chỉ số để đo lường về đặc điểm hình dáng của một phân phối xác suất. Cụ thể hơn, nó so sánh độ cao phần trung tâm của một phân phối so sánh với một phân phối chuẩn. Phần trung tâm càng cao và nhọn, chỉ số Kurtosis của phân phối đó càng lớn. Hay nói cách khác, kurtosis đo lường độ “béo” phần đuôi của một phân phối xác suất. Cái đuôi càng “béo”, kurtosis càng lớn. Kurtosis của một mẫu có công thức như sau:
n
Kurtosis
nn 1
n1n2n3
i 1
X X
i
4
n
1
i 1
X X
i
4
s4
n
s4
n : Cỡ mẫu.
Xi: giá trị mẫu quan sát thứ i.
X : giá trị trung bình mẫu.
s : độ lệch chuẩn mẫu có hiệu chỉnh.
Tính chất của Kurtosis:
Về mặt tính toán giá trị của độ nhọn (kurtosis), hầu hết trong các phần mềm xử lý số liệu đều có các hàm để tính, điều cần quan tâm ở đây là các tính chất liên quan tới giá trị của độ nhọn (kurtosis). Ở đây tính chất của độ nhọn (kurtosis) xoay quanh 3 vấn đề:
excess kurtosis
hình dạng của phân phối xác suất với excess kurtosis dương/âm ?
excess kurtosis bao nhiêu thì được coi là đáng kể ?
Tính chất: phân phối chuẩn có kurtosis = 3.
Định nghĩa của excess kurtosis: lấy kurtosis của phân phối trừ đi 3. Excess kurtosis dương có nghĩa là kurtosis của phân phối lớn hơn 3, excess kurtosis âm nghĩa là kurtosis của phân phối nhỏ hơn 3. Cụ thể hơn, phân phối có:
excess kurtosis dương được gọi là leptokurtic (“lepto” nghĩa là gầy)
excess kurtosis bằng 0 được gọi là mesokurtic
excess kurtosis âm được gọi là platykurtic (“platy” nghĩa là “rộng”).
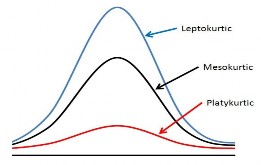
Hình 4.12 : Phân bố dữ liệu theo Kurtosis.
Ví dụ 4.20 Đồ thị của một phân phối chuẩn chuẩn hóa (µ = 0, σ = 1), một phân phối leptokurtic
và một phân phối platykurtic có hình dạng như sau:
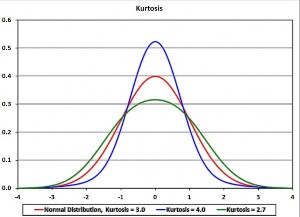
Hình 4.13 : Phân bố dữ liệu theo Kurtosis.
Phân phối chuẩn có kurtosis 3,0, hay zero excess kurtosis. Phân phối leptokurtic có kurtosis 4,0, hay excess kurtosis +1.0
Phân phối platykurtic có kurtosis of 2,7, hay excess kurtosis -0.3
Lưu ý, tuy trên đồ thị không thể hiện rõ lắm, nhưng phân phối leptokurtic có phần đuôi (phần lớn hơn +4 và nhỏ hơn -4) “béo” hơn phân phối chuẩn khoảng gấp đôi, và phân phối platykurtic có phần đuôi “mỏng” hơn phân phối chuẩn khoảng một nửa.
Excess kurtosis được tính là đáng kể nếu giá trị tuyệt đối của nó lớn hơn hoặc bằng 1.0; vd: kurtosis > 4.0 (excess positive kurtosis > 1.0) hoặc kurtosis < 2.0 (excess negative kurtosis < - 1.0).
4.2.2 Độ lệch – Skewness
Độ lệch (skewness) của một phân phối xác suất đo lường sự đối xứng của phân phối đó. Giá trị tuyệt đối của độ lệch càng cao thì phân phối đó càng bất đối xứng. Một phân phối đối xứng có độ lệch bằng 0. Công thức toán học của độ lệch là:
n
X X
i
3
n
X X
i
Skewness
i 1 i 1
n
n1n2
s3
1
3
n
s3
n : Cỡ mẫu.
Xi: giá trị mẫu quan sát thứ i.
X : giá trị trung bình mẫu.
s : độ lệch chuẩn mẫu có hiệu chỉnh.
Các tính chất của độ lệch (Skewness) :
hình dạng của một phân phối có độ lệch dương (positive skewness) hoặc độ lệch âm
(negative skewness)
độ lệch dương hay âm bao nhiêu thì được coi đáng kể
một số tính chất của phân phối có độ lệch dương hoặc độ lệch âm
Độ lệch dương có nghĩa là các giá trị cực lớn hơn giá trị trung bình (mean) sẽ ở xa hơn so với giá trị cực nhỏ hơn giá trị trung bình (mean). Một đồ thị điển hình của một phân phối liên tục với độ lệch dương sẽ trông như thế này:
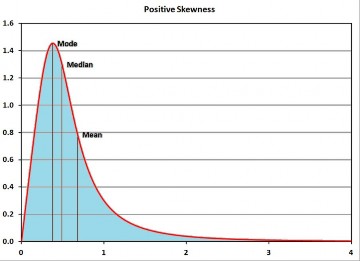
Hình 4.14 : Phân bố dữ liệu theo Kurtosis dương.
Tương tự, một đồ thị điển hỉnh của một phân phối liên tục có độ lệch âm sẽ có hình dạng như sau:
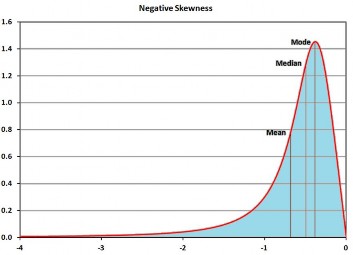
Hình 4.15 : Phân bố dữ liệu theo Kurtosis âm.
Chú ý: Độ lệch được coi là đáng kể nếu giá trị tuyệt đối của nó ≥0.5 (tức là giá trị ≤−0.5 hoặc ≥+0.5). Tính chất quan trọng của độ lệch được biểu thị qua 2 hình minh họa ở trên: với một phân phối có một mode duy nhất, bạn cần phải biết giá trị tương đối của mean, mode và media . Ở đây có một mẹo để ghi nhớ, đó là sắp xếp các từ này theo thứ tự bảng chữ cái, từ trái qua phải:
mean median mode
Nếu phân phối có độ lệch dương – nó sẽ bị lệch sang phải – khi đó ký hiệu sẽ là dấu >. Cụ thể:
mean > median > mode
Ngược lại, nếu phân phối có độ lệch âm – nó sẽ bị lệch sang trái – ký hiệu sẽ là < :
mean < median < mode
CHƯƠNG 5
ƯỚC LƯỢNG THAM SỐ
Mục lục chương 5
5.1. Các tiêu chuẩn ước lượng 77
5.2. Khoảng tin cậy cho giá trị trung bình 79
5.3. Khoảng tin cậy cho độ lệch hai giá trị trung bình 81
5.4. Khoảng tin cậy cho giá trị tỷ lệ 83
5.5. Khoảng tin cậy cho độ lệch hai giá trị tỷ lệ 85
5.6. Khoảng tin cậy cho giá trị phương sai 85
5.7. Khoảng tin cậy cho giá trị dự báo 87
5.1. CÁC TIÊU CHUẨN ƯỚC LƯỢNG.
Cho tổng thể đặc trưng bởi biến ngẫu nhiên X , và X1 , X2 ,..., Xn là các biến ngẫu nhiên quan sát từ
tổng thể có phân phối xác suất với tham số chưa biết. Thống kê TnT X1, X2, ..., Xn
dùng để
ước lượng cho gọi là một hàm ước lượng. Với mỗi bộ giá trị quan sát x1, x2,..., xnthì giá trị
t T x1, x2,..., xngọi là giá trị ước lượng cho tham số
5.1.1 Ước lượng không chệch.
Cho hàm ước lượng TnT X1, X2,..., XnTnđược gọi là
Ước lượng không chệch cho nếu ETn .
Nếu ETn thì ETn gọi là độ lệch của ước lượng. Tnđược gọi là ước lượng tiệm cận không
chệch cho nếu limETn .
n
Mức độ tốt của một số ước lượng được đánh giá bằng cách quan sát hành vi của nó trong sự chọn mẫu lặp lại. Chúng ta hãy xem xét sự giống nhau sau đây. Trên nhiều khía cạnh, thì sự ước lượng điểm là tương tự với việc bắn một khẩu súng vào một mục tiêu.
Ví dụ 5.1 Giả sử rằng một người đàn ông bắn một phát súng duy nhất vào một mục tiêu vàphát súng đó đã trúng ngay điểm đen. Liệu chúng ta có thể kết luận rằng ông ta là một xạ thủ cừ khôi? Câu trả lời là không - không một ai trong số chúng ta ắt sẽ bằng lòng giữ mục tiêu đó trong khi phát súng thứ hai được bắn đi. Đến khi nào mà sự chính xác của ông ta đã được quan sát thấy trong những lần bắn được lặp đi lặp lại, với tất cả phát súng đều trúng vào gần điểm đen, thì chúng ta ắt mới có thể tuyên bố rằng ông ta là một tay súng giỏi.
Về mặt hình ảnh ta có thể xem xét trường hợp ước lượng chệch và không chệch như sau:
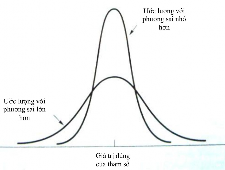
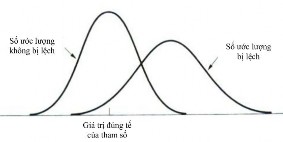
Khi ta đã đưa ra một ước lượng không chệch thì đặc trưng thứ hai đáng mong ước của một ước lượng là khoảng rộng (được đo bằng phương sai) của phân phối mẫu phải càng nhỏ càng tốt. Điều này đảm bảo rằng, với một xác suất cao, một sự ước lượng riêng lẻ sẽ rơi gần vào giá trị đúng của tham số. Các phân phối mẫu cho hai ước lượng không bị lệch, một với phương sai nhỏ và ước lượng kia với một phương sai lớn hơn, đương nhiên là chúng ta sẽ thích ước lượng với phương sai nhỏ hơn bởi vì những sự ước lượng có xu hướng nằm gần với giá trị đúng của tham số hơn là với phương sai lớn hơn.
Định lý. Giả sử X1, X2,..., Xnlà các biến ngẫu nhiên lấy từ tổng thể có trung bình là và độ lệch chuẩn là . Khi đó
X X1 X2 ... Xn là một ước lượng không chệch cho .
n
S
ˆ
2
1
n
i
n
X X là một ước lượng tiệm cận không chệch cho .
2
2
i 1
S2Sˆ2là một ước lượng không chệch cho 2 .
n
n 1
5.1.2 Khoảng tin cậy.
Khi xây dựng một ước lượng khoảng cho một tham số, chúng ta xác định hai điểm mà bên trong khoảng đó chúng ta mong đợi giá trị của tham số chưa biết đó rơi vào. Những ước lượng khoảng được xây dựng để khi chọn mẫu lặp lại thì với một tỷ lệ lớn (gần 1) của các khoảng này sẽ bao quanh tham số quan tâm. Tỷ lệ này được gọi là hệ số tin cậy, và khoảng tạo ra được gọi là khoảng tin cậy.
Đối với một cỡ mẫu cố định, bề rộng của khoảng tin cậy tăng lên khi hệ số tin cậy gia tăng, một kết quả mà đồng ý với trực giác của chúng ta. Chắc hẳn là nếu chúng ta mong muốn hơn rằng khoảng này sẽ bao quanh µ, thì chúng ta ắt sẽ tăng bề rộng của khoảng. Bởi vì chúng ta chỉ chấp nhận các khoảng tin cậy hẹp và hệ số tin cậy lớn hơn, nên chúng ta phải chỉ ra được một mối quan hệ giữa hệ số tin cậy, khoảng tin cậy. Lựa chọn hệ số tin cậy được sử dụng trong một tình huống cho trước được thực hiện bởi người làm thí nghiệm và tùy thuộc vào mức độ tin cậy mà người làm thí nghiệm mong muốn đặt ra trong ước lượng này. Hệ số tin cậy phổ biến nhất có lẽ là các khoảng tin cậy 95%. Việc sử dụng các khoảng tin cậy 99% là ít phổ biến hơn bởi vì bề rộng khoảng lớn hơn được tạo ra. Dĩ nhiên, lúc nào các bạn cũng có thể giảm bớt bề rộng này bằng cách gia tăng cỡ mẫu ݊.
Ngoài các khoảng tin cậy hai phía (mà chúng ta đơn giản gọi là các khoảng tin cậy), chúng ta cũng có thể xây dựng các khoảng tin cậy một phía cho những tham số.
Theo các tiêu chuẩn ước lượng, khi ta sử dụng bất kỳ hàm ước lượng Tnđể ước lượng cho tham số thì khoảng ước lượng có dạng Tn ,Tn giá trị sai số gọi là độ chính xác. Ở đây ta
không tuyệt đối tin rằng giá trị thật của tham số nằm trong khoảng Tn ,Tn , mà ta chỉ tin rằng
Trong đó 1
Nhận xét.
là độ tin cậy.
P Tn Tn 1
Khi độ chính xác càng nhỏ thì độ tin cậy càng thấp.
Khi Tnlà ước lượng vững cho , cố định độ chính xác thì độ tin cậy 1 tiến đến 1 khi cở mẫu thực nghiệm n tiến đến vô cùng.
Thông thường ta cố định độ tin cậy 1 rồi tìm khoảng tin cậy tương ứng.
5.2. Khoảng tin cậy cho giá trị trung bình.
5.3.1 Phân tích.
Gọi là trung bình của tổng thể chưa biết. Từ giá trị quan sát X1, X2,..., Xnđộc lập có cùng phân
phối chuẩn, ta xây dựng khoảng ước lượng cho với độ tin cậy 1 .
Hàm ước lượng Tn
X X1 X2 ... Xn , ta xây dựng khoảng ước lượng thỏa:
n
P X X 1
Định lý. Cho X1, X2,..., Xnlà biến ngẫu nhiên có quy luật phân phối chuẩn với kỳ vọng là và
phương sai là
2
, thì X có quy luật phân phối chuẩn X ~ N ,
n
2
.
Định lý. Cho X1, X2,..., Xnlà biến ngẫu nhiên có quy luật phân phối chuẩn với kỳ vọng là và
phương sai là 2, với X và S2là trung bình mẫu và phương sai mẫu (có hiệu chỉnh) ta có
X ~ N 0;1vàX ~ Tn1
n
S
n
Xét P X X 1 P X 1
n
n
n
Vì X ~ N ;2 Z X ~ N 0,1
n
2
n
Vì hàm ước lượng phụ thuộc vào 2 nên khoảng ước lượng cho chia làm hai trường hợp
Trường hợp 2 đã biết.
Ta có Z ~ N 0;1P z/2 Z z/2 1
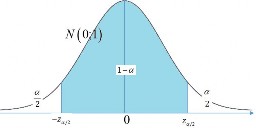
| X | | |
| 1 | nên ta có z /2 | z /2 n |
| n n n | n |
Có thể bạn quan tâm!
-
 Các Đại Lượng Đo Lường Mức Độ Tập Trung Của Dữ Liệu 55
Các Đại Lượng Đo Lường Mức Độ Tập Trung Của Dữ Liệu 55 -
 So Sánh Trung Bình (Mean), Trung Vị (Median), Yếu Vị (Mod)
So Sánh Trung Bình (Mean), Trung Vị (Median), Yếu Vị (Mod) -
 Các Khuynh Hướng Đo Vị Trí Tương Đối.
Các Khuynh Hướng Đo Vị Trí Tương Đối. -
 Khoảng Tin Cậy Cho Độ Lệch Hai Giá Trị Tỷ Lệ.
Khoảng Tin Cậy Cho Độ Lệch Hai Giá Trị Tỷ Lệ. -
 Kiểm Định Giả Thiết Cho Một Giá Trị Tỷ Lệ Tổng Thể.
Kiểm Định Giả Thiết Cho Một Giá Trị Tỷ Lệ Tổng Thể. -
 Kiểm Định Giả Thiết Cho Hai Giá Trị Tỷ Lệ Tổng Thể.
Kiểm Định Giả Thiết Cho Hai Giá Trị Tỷ Lệ Tổng Thể.
Xem toàn bộ 142 trang tài liệu này.
Và P
![]()
![]()
![]()
![]()
![]()
Trường hợp 2 chưa biết.
Trong thực tế ta thường xuyên không biết phương sai tổng thể 2, trong trường hợp này ta vẫn giả định tổng thể có quy luật phân phối chuẩn. Để đưa ra khoảng ước lượng cho ta cần tham số
n 1
n 1S 2
2
để ước lượng cho 2 , ta có:
X X . 1 X .
X
S S
![]()
n
n
n1S2
n
X
Trong đó
~ N 0;1và
n
~ 2,n1 nên Z
2
~T n1
![]()
S
n
/2
/2
Ta có Z ~T n1 P t n1 Z tn1 1 .

| | ||||
| X | | | n1 n1 | |
| n n | | n | 1 nên ta có | t/2 t/2 . n n |
Và P .
![]()
![]()
![]()
![]()
![]()
5.3.2 Quy tắc thực hành.
Khoảng ước lượng cho giá trị trung bình tổng thể với độ tin cậy 1 là khoảng X ; X
trong đó giá trị độ chính xác được tính theo công thức:
n 30 n 30
Trong đó z ; z
/2
n
/2
được tính theo phân phối chuẩn.
t n1 . S ; t n1 được tính theo phân phối Student
/2
/2
Ví dụ 5.2 Một công ty muốn ước lượng số tài liệu trung bình được chuyển bằng fax trong một ngày. Kết quả thu được từ 15 ngày cho thấy trung bình một ngày có 267 trang tài liệu được chuyển bằng fax, và theo kinh nghiệm từ các văn phòng tương tự thì độ lệch chuẩn là 32 trang. Với số tài liệu chuyển bằng fax trong một một ngày có quy luật phân phối chuẩn, thì với độ tin cậy 95% ta
ước lượng được số tài liệu trung bình chuyển trong ngày nằm trong khoảng:
X z . X z
/2
/2
.
Trong đó X 267, 32,n 15,1 95% z/2 1.96
Vậy khoảng ước lượng là 250,8055 283,1945
Ví dụ 5.3 Công ty điện thoại một thành phố muốn ước lượng thời gian trung bình của một cuộc điện đàm đường dài vào cuối tuần, mẫu ngẫu nhiên 20 cuộc gọi đường dài vào cuối tuần cho thấy thời gian gọi trung bình là 14,8 phút và độ lệch chuẩn là 5,6 phút. Như vậy với độ tin cậy 95% ta
ước lượng được thời gian gọi trung bình nằm trong khoảng.
X t n1 . S X t n1 . S
/2
/2
Trong đó X 14,8;S 5,6;n 20;1 95% tn1 2,093
/2
Vậy khoảng ước lượng là 12,1792 17,4208
![]()
![]()
n
n
2đã biết
z
/2
z
n
S
z
/2
n
2chưa biết
/2
t n1 . S
/2
![]()
n
n
n
n
n
5.3. Khoảng tin cậy cho độ lệch hai giá trị trung bình.
5.4.1 Phân tích
Gọi 1, 2là trung bình của 2 tổng thể, dựa trên việc khảo sát hai bộ mẫu độc lập của hai tổng thể ta mong muốn chỉ ra sự khác biết của hai trung bình tổng thể này. Ta xây dựng khoảng ước lượng cho 12với độ tin cậy 1 .
Hàm ước lượng là
Z X1 X2 và khoảng ước lượng thỏa
P X1X2 12X1X2 1
2 2
Định lý. Nếu hai mẫu độc lập được lấy ngẫu nhiên từ hai tổng thể có trung bình và phương sai lần lượt là 1, 2,1, 2, thì phân phối cho độ lệch của hai giá trị trung bình theo quy luật phân phối chuẩn với kỳ vọng và phương sai lần lượt là ( n1,n2lần lượt là cở mẫu của 2 mẫu 2 tổng thể)
2 2
1 2
n1 n2
5.4.2 Quy tắc thực hành
X1 X2
1 2 và
X1 X2
Trường hợp 1: Hai mẫu dữ liệu lấy độc lập.
Khoảng ước lượng cho độ chênh lệch giữa hai giá trị trung bình tổng thể 12là khoảng