Kiểm Định Giả Thiết Cho Hai Giá Trị Tỷ Lệ Tổng Thể.

Biết rằng các báo cáo trước đây khẳng định đường kính của tay đòn do nhà máy sản xuất có giá trị trung bình là 8,22mm, và độ lệch chuẩn là 0,02mm. Hỏi các báo cáo trước đây về phương sai của đường kính tay đòn có còn đúng với mức ý nghĩa  5% hay không.

Giải. Mô hình kiểm định có dạng là

1.

H : 0,02 và H : 0,02

2

2

2

2

0

1

Trong đó  là độ lệch chuẩn của đường kính tay đòn.

i

n

x 



2

2.

Trị thống kê của mô hình: (trường hợp trung bình tổng thể đã biết)  i 1 .

2

0

Trong đó x là đường kình của tay đòn thu từ mẫu dữ liệu,  8,22 ,  20,022. Ta có giá trị trị

i

thống kê:  29,75.

0

3.

4.

Phân vị sử dụng :  20 9,591 và  20 34,170 .

0,975

0,025

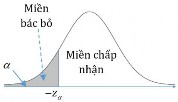
Kết luận: Vì 20  20 , nên ta kết luận không đủ bằng chứng bác bỏ báo cáo trước

0,975

0,025

đây về phương sai của đường kính tay đòn do nhà máy này sản xuất.

Ví dụ 6.6 Một nhà máy sản xuất tay đòn kim loại dùng trong hệ thống giảm xóc của xe máy, một mẫu gồm 15 tay đòn được chọn ngẫu nhiên,và được đo đạc đường kính. Kết quả theo đơn vị mm cho bởi bảng dữ liệu sau:

8.24

8.25	8.2	8.23	8.24
8.21	8.26	8.26	8.2	8.25
8.23	8.23	8.19	8.28	8.24

Có thể bạn quan tâm!

• Khoảng Tin Cậy Cho Độ Lệch Hai Giá Trị Trung Bình 81
• Khoảng Tin Cậy Cho Độ Lệch Hai Giá Trị Tỷ Lệ.
• Kiểm Định Giả Thiết Cho Một Giá Trị Tỷ Lệ Tổng Thể.
• Kiểm Định Giả Thiết Cho Hai Phương Sai Tổng Thể
• Thống kê ứng dụng trong kinh tế và kinh doanh - Trường ĐH Văn Lang - 16
• Thống kê ứng dụng trong kinh tế và kinh doanh - Trường ĐH Văn Lang - 17

Xem toàn bộ 142 trang tài liệu này.

Ví dụ 6.7 Một xí nghiệp sản xuất xi măng đã xác nhận rằng bê tông được làm từ xi măng của xí nghiệp có sức chịu nén kg / cm2khá ổn định theo tiêu chuẩn xây dựng là sức chịu nén dao động

quanh giá trị trung bình với độ lệch 10 kg / cm2. Khảo sát trên n 10 mẫu bê tông đo tạo ra một

số trung bình và phương sai lần lượt bằng với X 312;S2195. Liệu có đủ bằng chứng bác bỏ sự xác nhận của nhà máy này không rằng sức chịu nén của bê tông là không ổn định, với mức ý nghĩa 5%.

Giải: Mô hình kiểm định trong trường hợp này có dạng

1.

H : 10 và H : 10

2 2

2 2

0

1

2.

Trị thống kê dùng trong mô hình này là  

n 1S 2

0

Trong đó n 10;010;S 195 , nên trị thống kê  17,55 .

2

3.

4.

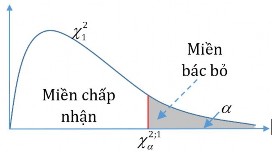
Mức ý nghĩa của kiểm định là 5% tương ứng phân vị n1 9

 0,05

16,919 .

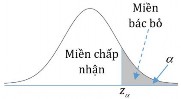
Kết luận : vì trị thống kê cao hơn phân vị (  9) nên ta hoàn toàn có thể bác bỏ khẳng

0,05

định của nhà máy này về bê tông của họ.

6.5. KIỂM ĐỊNH GIẢ THIẾT CHO HAI GIÁ TRỊ TỶ LỆ TỔNG THỂ.

6.5.1 Kiểm định giả thiết so sánh 2 tỷ lệ tổng thể sử dụng phân phối chuẩn.

i. Phân tích.

Xét hai tổng thể và một đặc trưng A , mỗi phần tử trong tổng thể chỉ mang hai tính chất là có tính chất A hoặc không có tính chất A . Xét trên hai mẫu cụ thể lấy từ mỗi tổng thể, ta cần kiểm định

giả thiết tỷ lệ phần tử có tính chất A trong hai tổng thể này có bằng nhau hay không với mức ý nghĩa  .

Gọi

f1 ; f2 là tỷ lệ phần tử mang đặc trưng A của hai mẫu, (theo chương 5) ta có :

n

p1 1 p1 ;

p2 1 p2 

f1 ~ N p1 ;

1

f2 ~ N p2 ; 

n

2 

Vậy f 

p ; p1 1 p1 p2 1 p2 , nên ta có

1 f2 ~ N p1 2



n1 n2 

p11 p1p21 p2

n1

n2



zf1f2p1p2

~ N 0;1

f 1 f 11

n n 

1 2 

Kết hợp giả thiết H0 : p1 p2 và gọi f là tỷ lệ phần tử mang đặc trưng A của cả hai mẫu dùng để ước lượng cho p1 và p2 . Ta có

f 1 f f 1 f 

n1

n2

z f1 f2

f1 f2

~ N 0;1

z là trị thống kê cho mô hình kiểm định giả thiết về sự bằng nhau của 2 tỷ lệ phần tử mang đặc trưng A trên hai tổng thể.

1. Giả thiết không H0 : p1 p2

2. Giả thiết đối

3. Trị thống kê

Với f1 ; f2 : tỷ lệ phần tử mang tính chất A trên mỗi mẫu. Với f : tỷ lệ phần tử mang tính chất A của 2 mẫu :

n1 n2

Trị thống kê : z 

f n1 f1 n2 f2

f1 f2 

4.

Trong đó f là tỷ lệ phần tử loại A của 2 mẫu lấy trên hai tổng thể. Miền bác bỏ.

Trị thống kê có quy luật phân phối chuẩn : z ~ N 0;1

Kiểm định 2 phía Kiểm định 1 phía Kiểm định 1 phía

ii. Mô hình kiểm định.

Kiểm định hai phía

Kiểm định một phía
H1 : p1 p2	H1 : p1 p2 H1 : p1 p2

f 1 f 11

n n 

1 2 

Đối thiết : H1 : p1 p2

Bác bỏ H0 khi:

z z /2



z z

Đối thiết : H1 : p1 p2

Bác bỏ H0 khi:

z z

Đối thiết : H1 : p1 p2

Bác bỏ H0 khi:

z z

 /2

Ví dụ 6.8 Một nguời quản lý bệnh viện nghi ngờ rằng trễ hạn trong việc thanh toán các hóa đơn viện phí đã gia tăng trong năm vừa qua. Hồ sơ lưu trữ của bệnh viện cho thấy rằng các hóa đơn của 48 trong số 1284 người nhập viện trong tháng Tư đã trễ hạn trong hơn 90 ngày. Con số này so với 34 trong số 1002 người nhập viện trong cùng tháng này năm trước đó. Liệu những dữ liệu này có cung cấp đủ bằng chứng để cho thấy có một sự gia tăng trong tỷ lệ trễ hạn thanh toán vượt quá 90 ngày không? Hãy kiểm định qua việc sử dụng  0,10 .

Giải: Vì chúng ta muốn kiểm định có một sự gia tăng trong tỷ lệ, nên mô hình kiểm định có dạng 1. H0 : p1 p2 và H0 : p1 p2

(trong đó chỉ số 1 tương trưng số liệu năm cũ và chỉ số 2 chỉ số liệu cho năm nay)

2.

Trị thống kê trong mô hình là : z 

f1 f2 

Trong đó f 34

1

1002 1284 2286

; f 48 ; f 82 ;n 1002;n 1284 , vậy z 0,45

2

1

2

3. Với mức ý nghĩa  0,10 ta có z 1,65 ,

4. Kết luận: z znên không đủ bằng chứng cung cấp cho việc khẳng định năm nay số lượng hóa đơn trả chậm gia tăng so với năm ngoái với mức ý nghĩa 10%.

f 1 f 11

n n 

1 2 

6.5.2 Kiểm định giả thiết so sánh 2 tỷ lệ tổng thể sử dụng phân phối chi bình

phương

i. Phân tích.

Thay vì dùng kiểm định z cho hai tỷ lệ tổng thể thông qua việc so sánh trực tiếp hai giá trị tỷ lệ. Ta có thể dùng kiểm định  bằng cách sử dụng bảng 2 chiều bai gồm tần số thành công và không

thành công trong hai nhóm :

Biến trên cột
Biến trên hàng	Nhóm 1	Nhóm 2	Tổng
Thành công	X1	X2	X X1 X2
Không thành công	n1 X1	n2 X2	nX
Tổng	n1	n2	n n1 n2

Trong đó

X1 ; X2

: tần số thực tế thành công trong nhóm 1 và 2.

n1 X1 ;n2 X2 : tần số thực tế không thành công trong nhóm 1 và 2.

n1 ;n2

: cỡ mẫu nhóm 1 và 2.

Mô hình kiểm định : so sánh 2 tỷ lệ thành công.

ii. Mô hình kiểm định

1. Giả thiết : H0 : p1 p2 (trong đó p1 ; p2 :tỷ lệ thành công trong tổng thể 1 và 2)

2. Đối thiết : H1 : p1 p2

Cơ sở lý luận của mô hình kiểm định :

Nếu H0đúng, thì tỷ lệ thành công trên 2 tổng thể là như nhau, sự khác biệt là sai số tình cờ trên 2 nhóm khảo sát. Vậy để giảm sai số, ta dùng con số chỉ tỷ lệ thành công và không thành công của 2 nhóm kết hợp lần lượt là:

p X1 X2 X và 1 p 1 X

S n n n s n

1 2

Ta lập bảng tần số lý thuyết trên cơ sở giả thiết H0 xảy ra

Đặt Oij : là tần số thực tế trong bảng bảng khảo sát

Đặt Eij : là tần số lý thuyết khi giả thiết H0 xảy ra

O E 2

3. Trị kiểm định :  2ij ij ~  2;1

Eij

4. Trị tới hạn : Với mức ý nghĩa  , tra bảng Chi bình phương : 2,1 .



Đối thiết H1 : X ;Y không độc lập với nhau. Bác bỏ H khi: G  2;1 0 

	Biến trên cột
Biến trên hàn	Nhóm 1	Nhóm 2	Tổng
Thành công	n1pS	n2 ps	npS
Không thành công	n1 1ps 	n2 1ps 	n1ps 
Tổng	n1	n2	n n1 n2

Ví dụ 6.9 Một công ty sở hữu hai khu nghỉ dưỡng trên một hòn đảo du lịch đã tiến hành một cuộc khảo sát sự hài lòng của khách hàng sau khi họ nghỉ tại đây, trong bảng câu hỏi điều tra có câu hỏi về việc khác hàng có dự định quay lại đây một lần nữa không? Số liệu thu được cho trong bảng bên dưới. Với mức ý nghĩa 5%, có bằng chứng thống kê nào cho thấy có sự khác biệt trong mức độ hài lòng của khách hàng (đo bằng ý định họ sẽ quay trở lại) tại hai khu nghỉ dưỡng A và B hay không.

Khu nghỉ
Dự định quay lại	A	B	Tổng
Có	163	154	317
Không	64	108	172
Tổng	227	262	489

Giả thiết H0: p1p2( p1; p2là tỷ lệ khách hàng dự định quay lại khu nghỉ dưỡng A và B)

Đối thiết H1 : p1 p2

Bảng tần số thực tế

Khu nghỉ
Dự định quay lại	A	B	Tổng
Có	E11 163	E12 154	317	p 317 s 489

Không

E21 64	E22 108	172	1 p 172 s 489
Tổng	227	262	489

Bảng tần số lý thuyết

Khu nghỉ
Dự định quay lại	A	B	Tổng
Có	O 317 .227 11 489	O 317 .262 12 489	317
Không	O 172 .227 21 489	O 172 .262 22 489	172
Tổng	227	262	489

Trị kiểm định  2



O E

ij

ij



2

Eij

9,061

Trị tới hạn  2,1 3,84 và vì 22,1 nên bác bỏ giả thiết, chấp nhận đối thiết. Vậy có đủ bằng

0,05

0,05

chứng để khẳng định tỷ lệ khách muốn quay lại 2 khu nghỉ dưỡng này là khác nhau, mức độ hài

lòng của khách đối với hai khu nghỉ dưỡng là khác nhau.

6.6. KIỂM ĐỊNH GIẢ THIẾT CHO HAI TRUNG BÌNH TỔNG THỂ.

6.6.1 Phân tích.

Cho hai tổng thể định lượng, gọi 1;2là trung bình của 2 tổng thể. Với hai mẫu dữ liệu lấy trên hai tổng thể, ta cần kiểm định giả thiết về việc trung bình trên hai tổng thể này có bằng nhau hay không với mức ý nghĩa  .

Xét hai mẫu với trung bình mẫu, cỡ mẫu lần lượt là X1; X2

1 2

tổng thể đã có lần lượt là  2 ; 2 , ta có:

và n1 ;n2 . Giả sử phương sai trên hai

 2  2 

X1 ~ N 1 ;1; X2 ~ N 2 ;2

n1 n2 

 2  2 

Nên suy ra

X1 X2 ~ N 1 2 ;12, kết hợp giả thiết H0 : 1 2 , đặt:

n1 n2 



X1X212X1X2

z~ N 0;1

 2  2  2  2

1 2 1 2

n1 n2 n1 n2

z là trị thống kê trong mô hình kiểm định giả thiết H0: 12, khi biết phương sai hai tổng thể.

Kiểm định hai phía	Kiểm định một phía
H1 : 1 2	H1 : 1 2 H1 : 1 2

6.6.2 So sánh hai trung bình tổng thể khi biết phương sai.

1.Giả thiết không H0 : 1 2

2.Giả thiết đối

3.Trị thống kê

Với hai mẫu có dữ liệu như sau:

	Mẫu	Cỡ mẫu	Trung bình mẫu	Độ lệch chuẩn tổng thể
	I	n1	X1	1

II	n2	X2	 2
Trị thống kê : z X1X2  2  2 12 n1 n2 4.Miền bác bỏ Trị thống kê có quy luật phân phối chuẩn : z~ N 0,1 Kiểm định 2 phía Kiểm định 1 phía Kiểm định 1 phía Đối thiết : H1 : 1 2 Đối thiết : H1 : 1 2 Đối thiết : H1 : 1 2 Bác bỏ H0 khi: Bác bỏ H0 khi: Bác bỏ H0 khi: z z /2 z z z z z z  /2

1. Giả thiết không H0: 12

2. Giả thiết đối

3. Trị thống kê

Với hai mẫu có các dữ liệu như sau:

Trị thống kê : z 

X1 X2

4. Miền bác bỏ

Trị thống kê có phân phối chuẩn : z~ N 0,1.

Kiểm định 2 phía Kiểm định 1 phía

Kiểm định 1 phía

Đối thiết : H1: 12

Đối thiết : H1: 12

Đối thiết : H1: 12

6.6.3 So sánh hai trung bình tổng thể khi không biết phương sai và cỡ mẫu lớn.

Kiểm định hai phía

Kiểm định một phía
H1 : 1 2	H1 : 1 2 H1 : 1 2

Mẫu

Cỡ mẫu	Trung bình mẫu	Độ lệch chuẩn
I	n1 30	X1	S1
II	n2 30	X2	S2

12

S 2 S 2

n1 n2

Bác bỏ H0 khi:

z z

Bác bỏ khi:

z z



z z

/2

Bác bỏ H0 khi:

z z

 /2

6.6.4 So sánh hai trung bình tổng thể khi không biết phương sai, phương sai

1.Giả thiết không H0: 12

2.Giả thiết đối H0

3.Trị thống kê

Với hai mẫu có các dữ liệu như sau:

Với S 2 1 1 2 2

n 1S 2 n 1S 2

n1 n2 2

Trị thống kê : z 

X1 X2

X1 X2

S 2 S2



n1 n2

4.Miền bác bỏ

Kiểm định 2 phía

Trường hợp phân vị z~t n1n22.

Kiểm định 1 phía Kiểm định 1 phía

Đối thiết : H1: 12

Đối thiết : H1: 12

Đối thiết : H1: 12

bằng nhau và cỡ mẫu nhỏ.

Kiểm định hai phía

Kiểm định một phía
H1 : 1 2	H1 : 1 2 H1 : 1 2

Mẫu

Cỡ mẫu	Trung bình mẫu	Độ lệch chuẩn
I	n1 30	X1	S1
II	n2 30	X2	S2

S 2 1 1 

n n 

1 2 

Ví dụ 6.10 Một cửa hàng bán thức ăn nhanh đã cân nhắc sử dụng phiếu giảm giá để kích thích doanh số bán hàng của mình. Công ty đặc biệt quan tâm đến việc liệu có sự khác biệt giữa những người độc thân so với các cặp vợ chồng đối với việc dùng phiếu giảm giá không. Một cuộc thăm dò của người tiêu dùng đã yêu cầu họ trả lời câu hỏi "Bạn có sử dụng phiếu giảm giá thường xuyên?" Theo thang điểm số, trong đó 1 là đồng ý mạnh mẽ, 2 cho đồng ý, 3 cho trung lập, 4 cho không đồng ý, và 5 cho không đồng ý mạnh mẽ. Kết quả cuộc thăm dò được đưa ra trong bảng sau:

Người độc thân Cặp vợ chồng

n1 31

X 1 3,10

S1 1, 460

. n2 57 .

X2 2,43

S2 1,350

Theo dữ liệu thu được, hỏi có sự khác biệt về điểm đánh giá trung bình của hai nhóm ngườikhảo sát với mức ý nghĩa  5% hay không

Giải. Mô hình kiểm định trong trường hợp này 1. H0 : 1 2 và H1 : 1 2

Trong đó 1 ;2 là điểm trung bình của nhóm người độc thân và nhóm các các cặp vợ chồng cho

đối với phiếu giảm giá.

2.

Trị thống kê trong mô hình: (Không biết phương sai, cỡ mẫu lớn) z 

X1 X2

.

Trong đó theo dữ liệu đề bài n1 31 ; n2 57 ; X 1 3,10 ; X2 2,43 ; S1 1,460 ; S2 1,350 . Ta có giá trị của trị thống kê: z 2,111 .

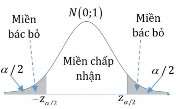
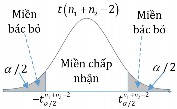
3. Phân vị sử dụng : Với mức ý nghĩa 5%, ta có: z/2 1,96 .

4. Kết luận: Vì z z /2 nên bác bỏ giả thiết H0 , nghĩa là hai nhóm người này có điểm đánh

giá trung bình cho phiếu khuyến mãi là khác nhau.

12

S2 S 2

n1 n2

Ví dụ 6.11 Một công ty hóa chất, quan tâm ảnh hưởng của chất xúc tác ảnh hưởng đến tốc độ trung bình của một quá trình hóa học. Một thử nghiệm được chạy trong nhà máy thí điểm và kết quả trong các dữ liệu thể hiện trong bảng sau. Dựa trên dữ liệu, hỏi có sự khác nhau giữa tốc độ trung bình của quá trình hóa học bị tác động bởi hai chất xúc tác khác nhau hay không với mức ý nghĩa  5% và phương sai về tốc độ phản ứng tương ứng 2 chất xúc tác giống nhau.

Quá trình

1	2	3	4	5	6	7	8
Chất xúc tác 1	91.5	94.18	92.18	95.39	91.79	89.07	94.72	89.21
Chất xúc tác 2	89.19	90.95	90.46	93.21	97.19	97.04	91.07	92.75

Giải. Mô hình kiểm định trong trường hợp này là:

1. H0 : 1 2 và H0 : 1 2 .

Trong đó 1 ;2 là tốc độ phản ứng trung bình khi cho tương ứng chất xúc tác 1 và 2.

2. Trị thống kê cho mô hình: (cỡ mẫu nhỏ, phương sai chưa biết và bằng nhau)

z X1 X2 

S 2 S 2

n1 n2

X1 X2 .

S2 1 1 

n n 

1 2 

Từ hai mẫu dữ liệu cho ta các kết quả về tốc độ của phản ứng hóa học ảnh hưởng bởi hai chất xúc

tác là:

Cỡ mẫu	Trung bình	Độ lệch chuẩn
Chất xúc tác 1	8	X1 92,255	S1 2,39
Chất xúc tác 2	8	X2 92,733	S2 2,98

Và phương sai chung của hai mẫu là:

n 1S 2 n 1S 2 7.2,392 7.2,982

S 2 

1 1 2 2 7,29625 .

n1 n2 2 8 8 2

Vậy trị thống kê của mô hình kiểm định là z 0,3539 .

 /2 0 ,025

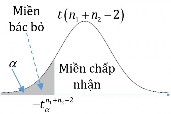
3. Phân vị sử dụng trong mô hình: t n1n22 t14 2.145 .

4. Kết luận: Vì

14

z t

0,025

nên không đủ bằng chứng để bác bỏ giả thiết H0 nghĩa là tốc độ trung

bình của phản ứng hóa học khi tác động bởi 2 chất xúc tác là như nhau.