Các Khuynh Hướng Đo Vị Trí Tương Đối.

S 

n 1

i

x X



i 1

75,2

1[182 1782168 1782184 1782190 1782170 1782174 1782]



Độ lệch tiêu chuẩn: S 75,2 8,6717

Hệ số biến thiên: V S 8,6718 4,87%

X 178

Ví dụ 4.11 Một dàn máy rạp hát gia đình trong một phòng nhỏ là cách dễ nhất và rẻ nhất để tạo ra âm thanh lập thể chi trung tâm giải trí gia đình. Một mẫu về giá được cho ở đây (Consumer Reports Buying Guide, 2004). Giá cả cho các mô hình có một đầu DVD và cho mô hình không có đầu DVD.

Mô hình có đầu DVD

Giá USD (X)	Mô hình không đầu DVD	Giá USD (Y)
Sony HT-1800DP	450	Pioneer HTP-230	300
Pioneer HTD-330DV	300	Sony HT-DDW750	300
Sony HT-C800DP	400	Kenwood HTB-306	360
Panasonic SC-HT900	500	RCA RT-2600	290
Panasonic SC-MTI	400	Henwood HTB-206	300

Có thể bạn quan tâm!

Xem toàn bộ 142 trang tài liệu này.

a) Tính giá trung bình cho các mô hình có đầu DVD và giá trung bình cho mô hình không có đầu DVD. Giá phải trả thêm để có đầu DVD trong dàn máy nhà hát gia đình là bao nhiêu?

b) Tính khoảng biến thiên, phương sai và độ lệch chuẩn của hai mẫu. Thông tin này cho bạn biết gì về giá cả của mô hình có đầu DVD và không có đầu DVD.

Giải.

Giá trung bình cho các mô hình có đầu DVD:

X 450 300 400 500 400 410

Giá trung bình cho mô hình không có đầu DVD: Y 300 300 360 290 300 310

b) Tính khoảng biến thiên, phương sai và độ lệch chuẩn của hai mẫu. Thông tin này cho bạn biết gì về giá cả của mô hình có đầu DVD và không có đầu DVD.

Mô hình có đầu DVD:

Khoảng biến thiên: RX XMax XMin 500 300 200

Phương sai:

S 2 1x

X 2

X n 1

i 1

1[450 4102300 4102400 4102500 4102400 4102] 4

5500

Độ lệch tiêu chuẩn: SX 

Mô hình không có đầu DVD:



47,162

Khoảng biến thiên: RY YMax YMin 360 290 70

Phương sai:

S 

n 1

i

y Y



i 1

800

Độ lệch tiêu chuẩn: SY 

1[300 3102300 3102360 3102290 3102300 3102]



28,28

Từ những thông tin trên cho thấy giá của mô hình có đầu DVD ổn định hơn giá của mô hình không có đầu DVD.

5500

S 2

800

4.3. Các khuynh hướng đo vị trí tương đối.

Đôi khi chúng ta muốn biết vị trí của một giá trị quan sát so với những giá trị quan sát khác trong một tập dữ liệu, cũng như việc đưa ra giá trị đo mức bình quân và phân tán không thể chỉ ra chính xác có những đột biến trong dữ liệu quan sát hay không thì các tham số về vị trí tương đối của bộ dữ liệu sẽ đưa ra đánh giá cho hai câu hỏi trên.

4.3.1 Phân vị.

Cho x1;x2;...;xnlà bộ giá trị quan sát đã được sắp theo thứ tự tăng dần. Phân vị thứ p là giá trị của ݔ sao cho có nhiều nhất là p% các giá trị đo lường là thấp hơn giá trị của ݔ và ít nhất là

100 p%là cao hơn giá trị của x .

Phân vị giúp ta nhận biết chính xác vị trí tương đối của lượng biến nằm đâu trong bảng số liệu.

Ví dụ 4.12 Sau khi kết thúc kỳ thi cuối kỳ môn xác suất thống kê, điểm một sinh viên đã được thông báo rằng số điểm là 6.5 đặt tại phân vị thứ 60 trong phân phối của những số điểm. Giá trị điểm khi so với điểm thi trung bình và độ lệch với điểm trung bình thì khẳng định tại phân vị thứ 60 có nghĩa là 60% những số điểm kiểm tra khác là thấp hơn số điểm của sinh viên này và 40% là cao hơn.

4.3.2 Tứ phân vị

Tứ phân vị

Là đại lượng mô tả sự phân bố và sự phân tán của tập dữ liệu. Tứ phân vị có 3 giá trị, đó là tứ phân vị thứ nhất (Q1), thứ nhì (Q2), và thứ ba (Q3). Ba giá trị này chia một bộ dữ liệu (đã sắp xếp dữ liệu theo trật từ từ bé đến lớn) thành 4 phần có số lượng quan sát đều nhau.

Min

25%

Max

Dữ liệu

Hình 4.6 : Biểu đồ tứ phân vị.

Phân vị thứ 25 và phân vị thứ 75, được gọi là tứ phân vị thấp và tứ phân vị cao (lower and upper quartiles), cùng với phân vị thứ 50 cũng chính là trung vị. Hai mươi lăm phần trăm các giá trị đo lường sẽ thấp hơn tứ phân vị thấp (đầu tiên), 50% sẽ thấp hơn trung vị (tứ phân vị thứ hai), và

75% các giá trị đo lường sẽ thấp hơn tứ phân vị cao (thứ ba). Như thế, trung vị và các tứ phân vị cao và thấp nằm tại những điểm trên trục ݔ sao cho diện tích bên dưới biểu đồ tần suất tương đối của dữ liệu được phân chia thành bốn diện tích bằng nhau,

25% dữ liệu

Min

Q1 Q2 Q3

Max

Hình 4.7 : Biểu đồ tứ phân vị.

Biểu đồ hộp biểu diễn tứ phân vị.

Box Plot giúp bạn biểu diễn các đại lượng quan trọng của dãy số như min, max, phân vị, khoảng tứ phân vị (Interquartile Range) một cách trực quan, dễ hiểu. Một Box plot có dạng như sau:

130

BIỂU ĐỒ PLOT BOX

Max

110

Min

Hình 4.8 : Biểu đồ tứ phân vị.

4.3.3 Giá trị z .

Một giá trị z của một số liệu trong bộ dữ liệu là đại lượng chỉ số tương đối về độ lệch chuẩn giữa một giá trị quan sát và trung bình của tập dữ liệu. Giá trị z của một số liệu ݔ định nghĩa bằng công thức :

z x X

Trong đó x : giá trị lượng biến quan tâm.

X : giá trị trung bình mẫu.

S : độ lệch chuẩn mẫu

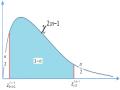
Định lý Tchebysheff

Một tổng thể bất chấp hình dạng phân phối, ít nhất 1 1.100% giá trị rơi vào khoảng m









so với giá trị trung bình.

P X m x X m 1 1

Bản thân các giá trị z chỉ đơn thuần cho thấy dữ liệu cần kiểm tra cao hơn hay thấp hơn trung bình bao nhiêu độ lệch chuẩn. Tuy nhiên, khi giá trị ݖ được sử dụng cùng với Định lý Tchebysheff, thì có thể đưa ra một số lời phát biểu thận trọng về vị trí tương đối của một dữ liệu quan sát.

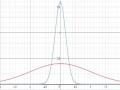
Hơn nữa, nếu dữ liệu có phân bố theo quy luật phân phối chuẩn (dạng phân phối hình chuông úp), thì Quy tắc Thực nghiệm có thể được dùng để đưa ra những lời phát biểu mạnh hơn về vị trí tương đối của một dữ liệu quan sát xét theo giá trị ݖ của nó.

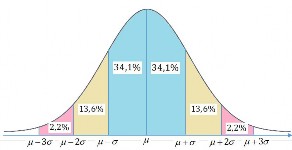
Hình 4.9 : Quy tắc 3 sigma.

Ví dụ 4.13 It nhất là 75% các giá trị quan sát trong một tập dữ liệu nằm trong phạm vi hai độ lệch chuẩn so với trung bình, nên các giá trị ݖ trong khoảng từ −2 đến +2 là rất có khả năng xảy ra, và như thế không phải là không bình thường.Và ít nhất là 8/9, hay rất có thể là tất cả, các giá trị quan sát nằm trong phạm vi ba độ lệch chuẩn so với trung bình, vì thế các giá trị ݖ trong khoảng từ 2 đến 3, ít có khả năng xảy ra hơn nhiều, và khi đó các giá trị ݖ cao hơn 3 rất không có khả năng xảy ra và phải được xem xét cẩn thận.

Giá trị ݖ cực kỳ lớn nêu lên câu hỏi về hiệu lực của một giá trị quan sát, tức giá trị quan sát này có thể đã được ghi nhận không đúng, hoặc nó có thể không thuộc về tổng thể mà chúng ta đã mong muốn lấy mẫu. Những giá trị quan sát với các giá trị ݖ hết sức lớn thường được gọi là giá trị dị biệt bởi vì chúng nằm cách xa trung tâm của tập dữ liệu. Những giá trị quan sát nằm cao hơn hay thấp hơn trung bình trong khoảng từ hai đến ba độ lệch chuẩn là những giá trị dị biệt có thể có, trong khi đó những giá trị quan sát nằm cao hơn hay thấp hơn trung bình nhiều hơn ba độ lệch chuẩn thì được xem là những giá trị dị biệt rõ ràng.

Ví dụ 4.14 Hãy xét một mẫu gồm ݊ = 10 giá trị đo lường:

3 2 0 15 2 3 4

Thoạt nhìn bạn có thể thấy giá trị đo lường x 15 là một giá trị dị biệt. Hãy tính giá trị z cho giá trị quan sát này, và hãy trình bày các kết luận của bạn. Đối với mẫu này ta có các đặc trưng như sau:

xi 33 X 3.3 (trung bình mẫu)

i 1





x 277 ; S 

1



11

10 1 



x X 18.6778 S 4.32(độ lệch chuẩn mẫu)

11





Với giá trị x 15 ta có trị z xX 15 3,3 2.71

4.32

Vì giá trị z nằm cách giá trị trung bình một khoảng là 2.71 lần độ lệch chuẩn nên có thể khẳng định x 15 là một giá trị đột biến. Nên chúng ta sẽ coi lại thủ tục lấy mẫu có sai số trong lần đo này không.

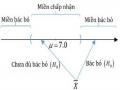
Ví dụ 4.15 Kết quả của một cuộc khảo sát quốc gia cho thấy trung bình người lớn ngủ 6,9 giờ mỗi đêm. Giả sử rằng độ lệch chuẩn là 1,2 giờ.

a) Sử dụng quy tắc Chebyshev để tính toán tỷ lệ phần trăm của những người ngủ từ 4,5 giờ đến 9,3 giờ.

b) Sử dụng quy tắc Chebyshev để tính toán tỷ lệ phần trăm của những người ngủ từ 3,9

đến 9,9 giờ.

c) Giả sử rằng số giờ ngủ có phân phối hình chuông. Sử dụng quy tắc thực nghiệm để tính toán tỷ lệ phần trăm của những người ngủ từ 4,5 đến 9,3 giờ mỗi ngày. So sánh kết quả mà bạn có được bằng cách sử dụng quy tắc Chebysev trong câu (a)?

Giải.

a) Sử dụng quy tắc Chebyshev để tính toán tỷ lệ phần trăm của những người ngủ từ 4,5 giờ đến 9,3 giờ.

z x1 X 4,5 6,9 2 độ lệch chuẩn và z x2 X 9,3 6,9 2 độ lệch chuẩn

1 S 1,2 2 S 1,2

Có ít nhất 1 1 .100% 1 1 .100% 75% .

z2 22 

1 

b) Sử dụng quy tắc Chebyshev để tính toán tỷ lệ phần trăm của những người ngủ từ 3,9

đến 9,9 giờ.

z x1 X 3,9 6,9 2,5 độ lệch chuẩn và z x2 X 9,9 6,9 2,5 độ lệch chuẩn

1 S 1,2 2 S 1,2

Có ít nhất 1 1.100% 1 1.100% 84% .

z2 

2,52 

1 

z1 2 và z2 2. Theo thực nghiệm: P 2 Z 295%

4.4. Hệ số tương quan của các bộ dữ liệu

Một trong những mục tiêu của khảo sát dữ liệu là tìm hiểu những mối tương quan giữa các bộ dữ liệu, và qua đó có thể tiên lượng một yếu tố phụ thuộc từ các yếu tố độc lập. “Mối tương quan” ở đây bao gồm các đặc điểm như mức độ tương quan (hệ số tương quan) và xây dựng một mô hình tiên đoán. Mô hình ở đây chính là hàm số nối kết hai biến với nhau.

Ví dụ 4.16 Liên hệ giữa độ tuổi và mật độ có nghĩa là chúng ta muốn biết mối tương quan giữa hai biến này ra sao và có thể sử dụng độ tuổi để tiên lượng mật độ xương cho một cá nhân hay không.

4.4.1 Hiệp phương sai.

Cho hai biến ngẫu nhiên X ,Y ; và nếu hai biến này hoàn toàn độc lập với nhau, chúng ta có thể phát biểu rằng phương sai của biến X Y bằng phương sai của X cộng với phương sai của Y

Var X Y Var X Var Y 

Nếu hai biến X ,Y có tương quan nhau, thì công thức trên được thay thế bằng một công thức khác với hiệp biến (hiệp phương sai, ký hiệu Cov X ,Y )

Var X Y VarX VarY 2Cov X ,Y 

Trong đó ta có hiệp phương sai được tính bằng công thức

Cov X ,Y E X EX Y EY 

Trong nội dung chương 1 ta có:

Var X Y E X Y E X Y 2E X EX Y EY 2

E X EX 2E Y EY 22E X EX Y EY 

VarX VarY 2E X EX Y EY 

Và ta có Cov X ,Y E X EX Y EY 

Một dạng công thức khác của hiệp phương sai là :

Cov X ;Y E XY E X .E Y 

Từ công thức trên ta có thể rút ra nhận xét như sau:

• Phương sai của biến ngẫu nhiên thì luôn dương nhưng hiệp biến thì mang dấu bất kỳ

• Hiệp biến là số dương nghĩa là độ lệch so với giá trị trung bình của ܺ tuân theo chiều

hướng thuận với ܻ

• Hiệp biến là số âm nghĩa là độ lệch so với giá trị trung bình của ܺ ngược lại theo chiều

hướng của ܻ

• Hiệp biến bằng 0 thì hai biến ܺ, ܻ không tương quan gì với nhau, tức Cov X ,Y 0

• Khi ܺ, ܻ độc lập với nhau nghĩa là ܺ, ܻ không tương quan.

• Nhưng ܺ, ܻ không tương quan chưa chắc đã độc lập với nhau.

Ví dụ 4.17 Cho hai biến ngẫu nhiên có bảng phân phối xác suất đồng thời như sau, ܺ, ܻ không

độc lập với xnhau

6	8	10	fX i 
1	0,2	0	0,2	0,4
2	0	0,2	0	0,2
3	0,2	0	0,2	0,4
fY j 	0,4	0,2	0,4	1

ܧܺ = (1 × 0.4) + (2 × 0.2) + (3 × 0.4) = 2

ܧܻ = (6 × 0.4) + (8 × 0.2) + (10 × 0.4) = 8

ܧ(ܻܺ) = (6 × 1 × 0.2) + (6 × 3 × 0.2) + (8 × 2 × 0.2) + (10 × 1 × 0.2) + (10 × 3 × 0.2) = 16

Vậy ܥ݋ݒ = ܧ(ܻܺ) − ܧܺ. ܧܻ = 0, vậy X,Y không tương quan nhau.

Đối với trường hợp khảo sát số liệu thực tế, biến ngẫu nhiên X có n số liệu Xi| i 1,nvà biến ngẫu nhiên Y có n số liệu Yi| i 1,nta có hiệp phương sai được tính thông qua công thức

Cov X ,Y 





n 1

i



x X y Y



i 1



Hoặc

Cov X ;Y 





n 1







x y 

1

i i

i 

i 1

i 1 i 1



i 





Nhận xét: Với việc đưa ra khái niệm hiệp phương sai sẽ gặp khó khăn khi nhận xét mối quan hệ của hai biến ngẫu nhiên về giá trị nhận được, vì hiệp phương sai của hai biến ngẫu nhiên phụ thuộc vào đơn vị của biến và khi đơn vị thay đổi dẫn đến độ lớn của hiệp phương sai thay đổi.

Ví dụ 4.18 Cho hai biến ngẫu nhiên ܺ – chỉ chiều cao của một người đơn vị là (m), và ܻ – chỉ cân nặng của một người đơn vị là (kg). Nếu ܺ chuyển sang đơn vị là (cm)

ܥ݋ݒ(10ܺ; ܻ) = ܧ(10ܻܺ) − ܧ(10ܺ). ܧܻ

= 10[ܧ(ܻܺ) − ܧܺ. ܧܻ] = 10ܥ݋ݒ(ܺ; ܻ)

Vậy việc tính hiệp phương sai giữa các biến ngẫu nhiên sẽ phụ thuộc vào đơn vị của các biến ngẫu nhiên, để khắc phục điều này ta xây dựng một chỉ số tương quan mới nhưng không lệ thuộc vào đơn vị của các biến ngẫu nhiên.

4.4.2 Hệ số tương quan.

Cho hai biến ngẫu nhiên ܺ, ܻ. Hệ số tương quan giữa ܺ, ܻ được ký hiệu là ߩ(ܺ, ܻ) có công thức là

ܥ݋ݒ(ܺ; ܻ)

ߩ(ܺ, ܻ)= ቐ√ܸܽݎܺ. ܸܽݎܻ ݇ℎ݅ ܸܽݎܺ; ܸܽݎܻ ≠ 0

0 ݇ℎ݅ ܸܽݎܺ = 0 ℎܽݕ ܸܽݎܻ = 0

Đối với trường hợp khảo sát số liệu thực tế, biến ngẫu nhiên X có n số liệu Xi| i 1,nvà biến ngẫu nhiên Y có n số liệu Yi| i 1,nta có hiệp phương sai được tính thông qua công thức :

 X ,Y 





i 1



X y



1n n 

Y





i 1

xi yi n xi yi 



i 1



i 1



i



x X



i



y Y



i 1

i



x X



i



y Y

i 1



Tính chất của hệ số tương quan:

−1 ≤ ߩ(ܺ; ܻ) ≤ 1

ߩ(ܺ; ܻ) = ±1 khi và chỉ khi tồn tại ܽ, ܾ ≠ 0 sao cho ܻ = ܽܺ + ܾ

Nếu giá trị của ߩ là dương, hai biến X ,Y cùng biến thiên theo một hướng; nếu giá trị của r là âm X ,Y liên hệ đảo ngược: tức khi khi X tăng thì Y giảm, và ngược lại.

Nếu  1;  1 (Biểu đồ 1a và 1b), mối liên hệ của y và x được hoàn toàn xác định; có

nghĩa là cho bất cứ giá trị nào của x, chúng ta có thể xác định giá trị của y.

Nếu  0 (Biểu đồ 1c), hai biến x và y hoàn toàn độc lập, tức không có liên hệ với nhau.

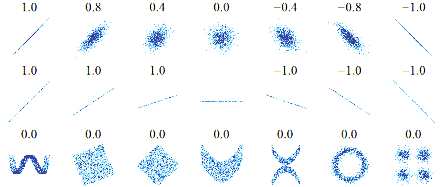
Hình 4.10 : Biểu đồ phân tán và hệ số tương quan.

Mặc dù rất khó đưa ra một nhận xét chắc chắn về giá trị của hiệp phương sai và mối quan hệ giữa các bộ dữ liệu, nhưng ta có thể đưa ra đánh giá thông qua bảng tương quan như sau



Mức độ tương quan
0  0.2			Rất yếu, tương quan không đáng kể.
0.2  0.4			Yếu, tương quan thấp.
0.4  0.7			Vừa phải.
0.7  0.9			Mạnh, tương quan mạnh.
0.9 		1.0	Tương quan tuyến tính rất mạnh

Trọng lượng trung bình ܺത = ܧܺ = ହଵା଺଺ାସ଻ା...ାଽ଴ = 57.0

ଵହ

Phương sai của trọng lượng trung bình

ܸܽݎܺ =

15 − 1

[(51 − 57)ଶ+ (66 − 57)ଶ+. . . +(90 − 57)ଶ] = 163.6

Vòng eo trung bình ܻത = ܧܻ = ଻ଵା଼ଽା଺ସା...ାଽସ = 75.5

ଵହ

Phương sai của vòng eo trung bình

ܸܽݎܻ =

15 − 1

((71 − 75.5)ଶ+ (89 − 75.5)ଶ+. . . +(94 − 75.5)ଶ) = 122.6

Hiệp phương sai của hai đại lượng

(51 − 57)(71 − 75.5)+. . . (90 − 57)(94 − 57.7)

ܥ݋ݒ(ܺ; ܻ) =

= 71.2

Hệ số tương quan của 2 đại lượng

ߩ(ܺ; ܻ) = = = 0.92

√ܸܽݎܺ. ܸܽݎܻ √122.6 × 163.6

ܥ݋ݒ(ܺ; ܻ)

71.2

40 45 50 55 60 65 70 75 80 85 90

Ví dụ 4.19 Cân nặng và vòng eo. Số liệu sau đây được trích ra từ một nghiên cứu qui mô (trên 3000 người) ở Việt Nam về mối liên hệ giữa các chỉ số nhân trắc và bệnh tiểu đường. Trọng lượng và vòng eo của 15 đối tượng được đo lường và kết quả như sau

Trọng lượng (Kg)

51	66	47	54	64	75	54	52
Vòng eo (cm)	71	89	64	74	87	93	66	74
Trọng lượng (Kg)	53	52	46	48	63	40	90	53
Vòng eo (cm)	75	72	66	70	81	57	94	75

Hình 4.11 : Biểu đồ phân tán vòng eo và cân nặng

• Dựa vào hệ số tương quan ta thấy trong nhóm đối tượng này mối tương quan giữa cân nặng và vòng eo là rất cáo.

Xem tất cả 142 trang.

Ngày đăng: 06/11/2023