So Sánh Trung Bình (Mean), Trung Vị (Median), Yếu Vị (Mod)

Mixini: tổng tất cả lượng biến có cùng giá trị xi

4.1.3 Số trung nhân.

Trường hợp lượng biến quan sát không cùng gốc so sánh, mà lượng biến sau thay đổi phụ thuộc vào lượng biến trước, thì trung bình giữa các lượng biến được tính theo công thức trung bình nhân.

X n x1x2...xn

Trong đó X : trung bình nhân.

xi : lượng biến thứ i.

Giá trị trung bình nhân là một công cụ quan trọng trong tính toán hiệu quả hoạt động kinh tế bởi

sự ảnh hưởng của hệ số nhân gộp của các giá trị qua các thời kỳ, trong việc đo tốc độ phát triển

kinh tế được gọi là tốc độ tăng trưởng gộp hay tỉ suất lợi nhuận theo thời gian.

Vậy số tiền tăng trưởng mỗi năm sẽ là: Năm 1: $1001.03 $103.00

Năm 2: $1031.05 $108.15

Năm 3: $108.151.08 $116.80 Năm 4: $116.80 0.99 $115.63 Năm 5: $115.63 1.10 $127.20

Giá trị trung bình nhân hay tỉ suất lợi nhuận là:

1 4.93%.

Tỉ suất lợi nhuận hàng năm là 4.93%, gần bằng là 5% là giá trị được tính bằng phương pháp cộng. Trong ví dụ trên lợi nhuận không thay đổi đáng kể qua từng năm nên trung bình cộng và trung bình nhân gần bằng nhau. Tuy nhiên, nếu danh mục đầu tư của bạn có mức lợi nhuận thay đổi đáng kể qua các năm thì sự chênh lệch giữa hai phương pháp là khá lớn.

Ví dụ 4.2 Một người đem $100 đi đầu tư và nhận được mức lợi nhuận như sau:

Năm 1

Năm 2	Năm 3	Năm 4	Năm 5
3%	5%	8%	-1%	10%

Có thể bạn quan tâm!

• Biểuđồ Mứcchênhlệchgiữaphânphốichuẩnvà Student
• Tiêu Thức Bất Biến Và Tiêu Thức Biến Động.
• Các Đại Lượng Đo Lường Mức Độ Tập Trung Của Dữ Liệu 55
• Các Khuynh Hướng Đo Vị Trí Tương Đối.
• Khoảng Tin Cậy Cho Độ Lệch Hai Giá Trị Trung Bình 81
• Khoảng Tin Cậy Cho Độ Lệch Hai Giá Trị Tỷ Lệ.

Xem toàn bộ 142 trang tài liệu này.

5 1.031.051.08.991.10

Trong ví dụ trên giá trị trung bình cộng là 



Tuy nhiên giá trị đúng là:

Năm 1: $1001.10 $110.00 Năm 2: $1102.5 $275.00 Năm 3: $2750.7 $192.50

Năm 4: $192.501.10 $211.75

10150 30 10

4

35%



Giá trị trung bình nhân hay tốc độ tăng trưởng là 20.6%, nhỏ hơn rất nhiều so với 35% được tính

bằng phương pháp cộng.

Ví dụ 4.3 Một nhà đầu tư nắm giữ một mã cổ phiếu biến động mạnh. Trong lần đầu tiên ông ta đã đầu tư $100, giá tăng rất mạnh nhưng sau đó có một đợt giảm nhanh. Mức lợi nhuận đem lại như sau:

Năm 1

Năm 2	Năm 3	Năm 4
10%	150%	-30%	10%

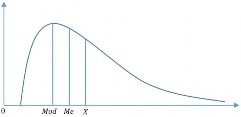
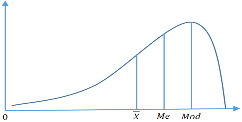
4.1.4 Yếu vị (Mod).

Yếu vị là biểu hiện của một lượng biến được gặp nhiều nhất trong tổng thể. Nếu xác định trên đồ thị với trục tung là tần số, trục hoành là lượng biến thì ta có thể nói yếu vị là hoành độ của điểm có tung độ cao nhất.

i. Trường hợp lượng biến rời rạc:

X

x1 x2

n

n1 n2

… xk

… nk

Mod xisao cho niMaxn1;n2;...;nk

ii. Trường hợp lượng biến liên tục

Khảo sát giá trị lượng biến trên việc phân tổ giá trị ta có bảng số liệu có dạng

Xx1; x2

x2;x3

… xk;xk1 

n

n1

n2

…

nk

Việc xác định giá trị Mod qua hai bước:

Bước 1 : Xác định tổ chứa Mod

o Trường hợp số liệu phân tổ có khoảng cách bằng nhau. Tổ chứa Mod là tổ có tần số lớn nhất.

o Trường hợp số liệu phân tổ có khoảng cách không bằng nhau.

i

h

Tổ chứa Mod là tổ có mật độ lớn nhất, với mật độ tổ cho bởi M

ni , trong đó: n là

i

i

tần số của tổ thứ i và hi là chiều dài của tổ thứ i

Bước 2 : Xác định giá trị Mod trong tổ:

ModX X

Mo M

MMo MMo1

MoMin

h

Mo Mo1

M

M

Mo

M

Mo1



Trong đó XMoMin: cận dưới của tổ chứa Mod.

hMo MMo MMo1

MMo1

: chiều dài của tổ chứa Mod.

: mật độ tổ chứa Mod.

: mật độ tổ trước tổ chứa Mod.

: mật độ tổ sau tổ chứa Mod.

Chú ý : Công thức này có thể dùng trong cả hai trường hợp đối với phân tổ đều và không đều,

nhưng trong trường hợp phân tổ đều ta có thể thay mật độ tổ bằng tần số tổ để công thức đơn

giản hơn.

Ví dụ 4.4 Có tài liệu về doanh thu của 79 cửa hàng trong tháng 10 năm 2009 như bảng dưới. Xác

định Mod của dữ liệu.

Doanh thu (triệu

đồng)

Cửa hàng ( ni )	Khoảng cách tổ	Mật độ phân phối M ni i h i
200 – 400	8	200	0,04
400 – 500	12	100	0,12
500 – 600	25	100	0,25
600 – 800	25	200	0,125

800 – 1000

9	200	0,045
Tổng	79

Tổ 3 là tổ chứa mốt. Vì đây là trường hợp phân tổ không đều nên dùng mật độ tổ để tìm mốt

MMo MMo1

ModX X

MoMin

h

Mo M

Mo Mo1

M

M

Mo

M

Mo1



0,25 0,12

500 100 0,250,120,250,125

550,980

4.1.5 Số trung vị (Median)

Số trung vị là lượng biến của đơn vị tổng thể đứng ở vị trí giữa trong dãy số lượng biến đã được sắp xếp theo thứ tự tăng dần. Số trung vị phân chia dãy số lượng biến làm hai phần (phần trên và phần dưới số trung vị) mỗi phần có số đơn vị tổng thể bằng nhau.

i. Trường hợp lượng biến rời rạc.

Khi lượng biến rời rạc ta sắp xếp giá trị lượng biến theo thứ tự tăng dần và đánh chỉ số cho

lượng biến.

Trường hợp tổng số quan sát là số lẻ ( n lẻ) : Me xn1

x x

2

Trường hợp tổng số quan sát là số chẵn ( n chẵn) : Me n/2 n2/2

2

ii. Trường hợp lượng biến liên tục.

Khảo sát giá trị lượng biến trên việc phân tổ giá trị ta có bảng số liệu có dạng

X

x1;x2		x2;x3		…	xk	;xk	1	
n	n1	n2		…		nk

Việc xác định giá trị trung vị qua hai bước

Bước 1: xác định tổ chứ trung vị.

Tổ chứ trung vị là tổ chứa giá trị n/ 2 trong trường hợp tổng số quan sát là chẵn hoặc là tổ chứa giá trị n1/ 2 nếu tổng số quan sát là số lẻ.

Ví dụ 4.5 Có tài liệu về doanh thu của 79 cửa hàng trong tháng 10 năm 2009 như bảng dưới. Xác

định trung vị của dữ liệu.

Me X

MeMin

hMe S S

n

Me 

2 Me 1 





Trong đó XMeMin: Cận dưới tổ chứa trung vị.

hMe nMe S

SMe1

: chiều dài tổ chứa trung vị.

: tần số tổ chứ trung vị.

: tổng số lượng quan sát.

: tổng tần số tất cả các tổ cho tới tổ trước tổ chứ trung vị.

Bước 2: xác định giá trị trung vị trong tổ.

Doanh thu (triệu đồng)

Cửa hàng ( ni )	Tần số cộng dồn
200 – 400	8	8
400 – 500	12	20

500 – 600

25	45
600 – 800	25	70
800 – 1000	9	79
Tổng	79

Tổ 3 là tổ chứa trung vị. Ta có trung vị của dữ liệu

MeX X

MeMin

hMe S S

n

Me 

2 Me1 

500 1007920578



25 2







Ví dụ 4.6 Có tài liệu tổng hợp về doanh số bán của 50 trạm xăng dầu thuộc tỉnh X trong tháng

10/2012 như sau:

Doanh số bán (triệu đồng)

Số trạm
200 – 300	8
300 – 400	10
400 – 500	20
500 – 600	7
600 – 700	5
Tổng	50

Xác định trung bình, trung vị và mốt của tập số liệu trên.

Trung bình

X i 1

xi ni

k

i

k

n

2508 35010 45020 5507 6505

50

432

i 1

Trung vị : Tổ 3 là tổ chứa trung vị

Me X

MeMin

hMe S S

n

Me 

2 Me1 

400 1005018500



7

2







Mode : Tổ 3 là tổ chứa mốt

Vì đây là trường hợp phân tổ đều nên dùng tần số tổ để tính mốt

MMo MMo1

ModX X

MoMin

h

Mo M

400 100

Mo Mo1

M

M

Mo

M

Mo1



20 10

2010207

443,478

Giải. Ta lập bảng:

Doanh số bán (triệu đồng)

Trị trung bình tổ	Số trạm
200 – 300	250	8
300 – 400	350	10
400 – 500	450	20
500 – 600	550	7
600 – 700	650	5
Tổng		50

iii. So sánh trung bình (Mean), trung vị (Median), yếu vị (Mod)

Trung bình lẫn trung vị đều là hai thước đo tốt đối với trung tâm của một bộ số liệu, nhưng trung vị phản ánh mức độ tập trung đo lường mạnh hơn vì không bị ảnh hưởng bởi biến động của số liệu, nhưng trung vị lại không phản ánh được sự thay đổi của số liệu. Yếu vị rất hữu ích đối với dữ liệu có kiểu dữ liệu phân loại (nominal), đối với các dữ liệu có kiểu phân loại ta không thể dùng trung bình hay trung vị vì nó không có ý nghĩa gì mà ta phải dùng yếu vị.

Nếu phân phối của một bộ dữ liệu đối xứng qua trung bình của nó − nghı̃a là hai nửa bên trái và bên phải là những hình ảnh phản chiếu − thì số trung bình và số trung vị bằng nhau [Hình 4.2].

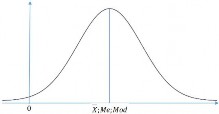
Hình 4.2 :Phân phối dữ liệu đối xứng

Nếu phân phối không đối xứng và cónhững quan sát thái cực nằm ở đuôi bên phải của phân phối này, thì phân phối này được gọi là bị lệch xiên về bên phải [Hình 4.3]. Bởi vì những giá trị thái cực lớn ở đuôi trên của phân phối này làm tăng tổng số của các giá trị đo lường, nên số trung bình chuyển dịch sang phải. Số trung vị không bị ảnh hưởng bởi những giá trị thái cực này, bởi vì giá trị tần số của các giá trị đo lường không được sử dụng trong việc tính toán số trung vị. Tương tự, nếu một phân phối bị lệch xiên về bên trái, thì số trung bình chuyển dịch sang trái [Hình 4.4].

Hình 4.3 :Phân phối dữ liệu lệch trái Hình 4.4 :Phân phối dữ liệu lệch phải

Ví dụ 4.7 Giả sử rằng bạn chạy 100m trong sáu lần, mỗi lần chạy bạn dùng đồng hồ đo lại thời gian chạy (giây) và kết quả 6 lần chạy của bạn gồm sáu giá trị như sau x25.1; 21.2; 17.9; 23.0; 24.6; 19.5. Phân tích các đặc trưng ta có:

Thời gian chạy trung bình (mean) là 21.9 giây

Giá trị trung vị (median) là 22.1 giâyThời gian chạy nhiều nhất (maximum) là 25.1 giây và ít nhất (minimum) là 17.9 giây.

Giả sử sau khi chạy hết 6 lần, bạn chạy tiếp lần thứ 7. Lần này đột nhiên chân bạn bị đau và bạn đi bộ thay vì chạy, kết quả thời gian của lần này là 79.9 giây. Bạn cố gắng thử thêm lần nữa và kết quả vẫn 79.9 giây. Ta có số liệu về 8 lần chạy như sau:

x 25.1; 21.2; 17.9; 23.0; 24.6; 19.5; 79.9; 79.9

Các giá trị Mean, Median và Mode so sánh giữa 2 bộ dữ liệu như sau:

Bộ 6 dữ liệu	Bộ 8 dữ liệu
Mean	21.9 giây	36.4 giây
Median	22.1 giây	23.8 giây
Mode		79.9 giây

Đối với 6 lần chạy đầu tiên thì thời gian chạy ổn định, còn 2 lần sau có sự khác biệt rất lớn so với 6 lần chạy ban đầu (2 giá trị này được xem là bất thường của dữ liệu). Nếu bạn không bị đau thì thời gian chạy dao động quanh Median. Theo bảng trên ta thấy rằng 2 số liệu sau không ảnh hưởng nhiều đến Median (từ 22.1 lên 23.8) nhưng ảnh hưởng rất lớn đến Mean (từ 21.9 lên 36.4) và Mode. Mặc dù Median có khả năng đo lường xu hướng tập trung của dữ liệu mạnh hơn Mean vì Median không bị ảnh hưởng bởi các dữ liệu bất thường nhưng nhiều người vẫn thích sử dụng

Mean để đo lường xu hướng tập trung của dữ liệu vì dễ tính hơn và không cần phải sắp xếp dữ

liệu như Median.

Ví dụ 4.8 Nếu dữ liệu mô tả giới tính là nominal và 1 là nam, 0 là nữ thì Mean hay Median là 0.5 không có ý nghĩa gì. Trong khi đó Mode cho biết tần suất nam hay nữ xuất hiện nhiều nhất trong bộ dữ liệu khảo sát.

4.2. Các khuynh hướng đo độ phân tán.

Một khi chúng ta đã xác định giá trị trung tâm và bình quân của một phân phối dữ liệu, bước tiếp theo là cung cấp các thước đo về độ biến thiên, hay độ phân tán của dữ liệu. Gồm có khoảng biến thiên, độ lệch tuyệt đối trung bình, phương sai, độ lệch chuẩn và hệ số biến thiên.

Độ biến thiên của dữ liệu dùng để đánh giá mức độ đại diện của của số bình quân đối với tổng thể nghiên cứu, nghĩa là độ biến thiên của dữ liệu càng lớn thì mức đại diện của bình quân cho tổng thể càng thấp và ngược lại. Độ biến thiên của dữ liệu trong dãy lượng biến sẽ cho thấy nhiều đặc trưng về phân phối của tổng thể hơn so với các giá trị trung tâm và bình quân, giúp ích nhiều trong việc điều tra chọn mẫu, chỉ ra mối quan hệ giữa các điều kiện khảo sát số liệu và dự đoán thống kê.

Hãy xét hai phân phối được trình bày trong hai hình dưới. Cả hai phân phối đều được đặt ở vị trí

có trung tâm tại X 4 , nhưng có sự khác biệt lớn về độ biến thiên của những giá trị đo lường

xung quanh số trung bình đối với hai phân phối này. Các giá trị đo lường trong hình thứ nhất thay

đổi xấp xỉ từ 3 đến 5; trong hình thứ hai, các giá trị đo lường thay đổi từ 0 đến 8.

Sự biến thiên là một đặc trưng quan trọng của dữ liệu. Nhưng việc dữ liệu phân tán giá trị rộng hay hẹp và quyết định về điều đó còn tùy thuộc vào đặc điểm của dữ liệu đang xét.

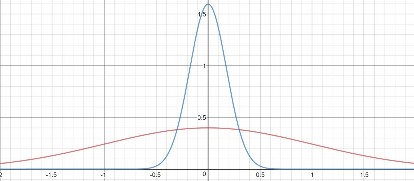
Hình 4.5 : Phân phối dữ liệu với độ lệch chuẩn khác nhau.

Ví dụ 4.9 Giả sử chúng ta đang chế tạo bu-lông, thì sự biến thiên quá mức trong đường kính của bu-lông sẽ kéo theo một tỷ lệ phần trăm cao của sản phẩm có khiếm khuyết. Mặt khác, khi chúng ta sử dụng một bài kiểm tra để phân biệt giữa những kế toán viên giỏi và kém, thì chúng ta sẽ không vui nhất nếu bài kiểm tra này lúc nào cũng mang lại những điểm kiểm tra với ít biến thiên, bởi vì điều này sẽ làm cho việc phân biệt trở nên rất khó khăn.

4.2.1 Khoảng biến thiên.

Khoảng biến thiên là độ dài khoảng giá trị mà lượng biến tối đa và tối thiều có thể nhận được.

R XMax XMin

Trong đó R : khoảng biến thiên.

XMax : lượng biến tối đa.

X Min : lượng biến tối thiểu.

4.2.2 Độ lệch tuyệt đối trung bình.

Độ lệch tuyệt đối bình quân là mức chênh lệch bình quân giữa các lượng biến và số bình quân cộng của các lượng biến đó.

n

d i 1

xi X

n

Trong đó d : độ lệch tuyệt đối trung bình.

X : trung bình cộng lượng biến.

Ưu điểm: Công thức độ lệch tuyệt đối trung bình cho chỉ chính xác giá trị lệch trung bình giữa

lượng biến và trung bình lượng biến, trong trường hợp bảng số liệu thực tế công thức dễ tính toán.

Nhược điểm: Công thức tính phụ thuộc vào dấu giá trị tuyệt đối, nên trong trường hợp khảo sát về mặt lý thuyết thì công thức không thể áp dụng và mở rộng.

4.2.3 Phương sai , độ lệch chuẩn.

Phương sai là bình quân cộng của bình phương các độ lệch giữa lượng biến với số bình quân của hiện tượng đó. Thước đo này sẽ tương đối lớn đối với dữ liệu biến thiên nhiều và tương đối nhỏ đối với dữ liệu biến thiên ít.

i. Phương sai tổng thể.

Phương sai tính trên toàn bộ số liệu tổng thể là phương sai tổng thể.

Công thức phương sai theo xác suất:

 2E X EX 2E X 2EX 2

Công thức phương sai theo tần số:

 

2

1

N

i

N

X X



2

i 1

Trong đó  2 : phương sai tổng thể.

N : tổng số liệu của tổng thể.

ii. Phương sai mẫu.

Phương sai mẫu được tính trên một mẫu số liệu, là đại lượng ước lượng cho phương sai tổng thể trong trường hợp không thể thu thập toàn bộ số liệu tổng thể.

S 

2

1

n 1



n

x X

i



2

i 1

Trong đó S 2 : phương sai mẫu.

݊ : tổng số liệu của mẫu.

iii. Độ lệch chuẩn.

Do trong cách tính của phương sai ta đã bình phương độ lệch lên, đồng nghĩa về mặt đơn vị phương sai không còn cùng đơn vị với đơn vị đo tổng thể, do đó để đưa ra một đại lượng chỉ chính xác độ lệch của lượng biến với trung bình lượng biến ta lấy căn của phương sai, đại lượng thu được gọi là độ lệch chuẩn.

i

N

X X



2

i 1

N

Độ lệch chuẩn tổng thể :  

1

n

n 1 i 1

i



x X



2

Độ lệch chuẩn của mẫu : S 

iv. Quy luật phân phối của phương sai mẫu.

Giả sử tổng thể X có quy luật phân phối chuẩn với X ~ N ;2, trên tổng thể này ta thu thập

một mẫu dữ liệu cỡ mẫu n gồm X1; X 2;,...; X n , thì ta có đại lượng phương sai mẫu S

n 1S 2

2

thỏa

2

~ 2;n1

Lưu ý.

Quy luật phân phối đồng thời trung bình mẫu và phương sai mẫu.

Giả sử tổng thể X có quy luật phân phối chuẩn với X ~ N ;2, trên tổng thể này ta thu thập một mẫu dữ liệu cỡ mẫu n gồm X1; X 2;,...; X n , thì ta có đại lượng trung bình mẫu X và phương

sai mẫu S 2 kết hợp thỏa

X   ~ Tn1

S

n

4.2.4 Hệ số biến thiên.

Hệ số biến thiên là tỷ số so sánh giữa độ lệch tiêu chuẩn (hoặc độ lệch tuyệt đối bình quân) với số bình quân cộng của các lượng biến.

Trong quá trình kết luận sự phân tán giá trị của bảng số liệu, thì bản thân giá trị của phương sai hay độ lệch chuẩn không thể nói lên mức độ phân tán của bảng số liệu là rộng hay hẹp, nên ta phải so sánh mức độ phân tán giá trị với mức độ bình quân của số liệu để đánh giá mức chênh lệch.

Hệ số biến thiên theo độ lệch tuyệt đối trung bình.

V d

X

Hệ số biến thiên theo độ lệch chuẩn.

V S

X

Trong đó V : hệ số biến thiên.

X : giá trị trung bình

d : độ lệch tuyệt đối trung bình.

S : độ lệch chuẩn

Ví dụ 4.10 Xét mẫu với giá trị dữ liệu: 182, 168, 184, 190, 170, và 174. Tính các giá trị: khoảng biến thiên, phương sai, và độ lệch tiêu chuẩn, hệ số biến thiên.

Khoảng biến thiên: R XMax XMin 190 168 22

Phương sai: