Kiểm Định Giả Thiết Cho Một Giá Trị Tỷ Lệ Tổng Thể.

Giả thiết H0là một khẳng định mà nhà nghiên cứu không mong muốn ủng hộ. Giả thiết H0

được đặt ra để làm nền tảng tính toán cho bài toán kiểm định.

Đối thiêt H1là sự phủ nhận của giả thiết H0; nghĩa là, nếu giả thuyết không là sai, thì đối thiết phải là đúng. Và nhà nghiên cứu phải thu thập dữ liệu để cố gắng đạt được điều đó.

Quyết định bác bỏ hay chấp nhận giả thiết H0được căn cứ vào thông tin chứa trong một mẫu

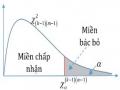
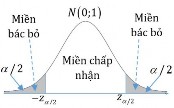
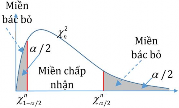
được lấy ra từ tổng thể. Các giá trị của mẫu được sử dụng để tính toán một con số duy nhất, gọi là trị thống kê. Toàn bộ tập hợp các giá trị mà trị thống kê kiểm định này có thể có được chia thành hai miền. Một miền, bao gồm các giá trị mà ủng hộ cho đối thiết H1, được gọi là miền bác bỏ.

Miền kia, bao gồm các giá trị mà không mâu thuẫn với giả thuyết không, được gọi là miền chấp nhận.

Miền chấp nhận và bác bỏ được phân cách bởi một giá trị tới hạn của trị thống kê kiểm định đó. Nếu trị thống kê kiểm định này được tính từ một mẫu cụ thể có một giá trị nằm trong miền bác bỏ, thì giả thuyết không bị bác bỏ, và giả thuyết thay thế H1được chấp nhận. Nếu trị thống kê đó rơi vào miền chấp nhận, thì hoặc là giả thuyết không được chấp nhận hoặc trị thống kê đó bị đánh giá là không thuyết phục. Trong bất cứ trường hợp nào, thì sự thất bại trong việc bác bỏ H1 hàm ý rằng dữ liệu này không đủ bằng chứng để hỗ trợ H1.

Ví dụ 6.2 Khảo sát về điểm trung bình của sinh viên sau khi tốt nghiệp, của một khoa, của một trường Đại học. Chúng ta muốn biết điểm trung bình của sinh viên có khác 7,0 không. Thì giả thiết và đối thiết như sau:

Giả thiết H0 :  7,0 Đối thiết H1 :  7,0

Công việc kiểm định được thực hiện, bằng cách khảo sát 100 sinh viên về điểm trung bình. Và tính

trung bình điểm trung bình của 1 sinh viên, giá trị là X . Vì ta đang so giữa trung bình mẫu và trung bình tổng thể  7,0 , nên việc so sánh phải phù hợp với một sai số cho phép. Với sai số đó

ta mở ra một vùng giá trị xung quanh  7,0 . Nếu X không nằm trong vùng đó thì ta bác bỏ giả thiết H0, tức đối thiết H1đúng, còn ngược lại thì ta chưa đủ bằng chứng bác bỏ H0. Sơ đố như sau:

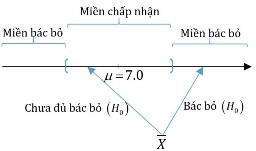
6.1.2 Sai lầm loại I và sai lầm loại II.

Những quyết định cho mô hình sẽ gồm các kết quả đúng và sai cho bởi bảng sau:

Thực tế giả thiết không

Quyết định

Đúng	Sai
Bác bỏ H0	Sai lầm loại I : 	Quyết định đúng
Chấp nhận H0	Quyết định đúng	Sai lầm loại II 

Có thể bạn quan tâm!

• Các Khuynh Hướng Đo Vị Trí Tương Đối.
• Khoảng Tin Cậy Cho Độ Lệch Hai Giá Trị Trung Bình 81
• Khoảng Tin Cậy Cho Độ Lệch Hai Giá Trị Tỷ Lệ.
• Kiểm Định Giả Thiết Cho Hai Giá Trị Tỷ Lệ Tổng Thể.
• Kiểm Định Giả Thiết Cho Hai Phương Sai Tổng Thể
• Thống kê ứng dụng trong kinh tế và kinh doanh - Trường ĐH Văn Lang - 16

Xem toàn bộ 142 trang tài liệu này.

Sai lầm loại I: Bác bỏ H0khi thực tế H0đúng. Xác suất của việc tạo ra một sai lầm loại I được biểu thị bởi ký hiệu  .

Sai lầm loại II: Chấp nhận H0khi thực tế H0sai. Xác suất của việc tạo ra một sai lầm loại II được biểu thị bởi ký hiệu  .

Mức độ thích hợp của một kiểm định thống kê được đo lường bởi xác suất tạo ra sai lầm loại I và sai lầm loại II. Bởi vì  là xác suất của việc bác bỏ H0khi thực tế giả thuyết này là đúng, cho nên đây là một đại lượng của cơ may bác bỏ sai H0. Bởi vì  là xác suất của việc chấp nhận H0khi

thực tế giả thuyết này là sai, cho nên phần bù của nó, 1  là xác suất của việc bác bỏ H0 khi thực

tế giả thuyết này là sai. Xác suất 1  được gọi là năng lực của sự kiểm định của mô hình.

Một cách thức khác để báo cáo kết quả kiểm định là thông qua giá trị p ( p -value). Xác suất  của việc tạo ra sai lầm loại I thường gọi là mức ý nghĩa của mô hình kiểm định, và trong quá trình kiểm định thì chúng ta có thể chọn các mức ý nghĩa khác nhau (ví dụ như  0,05z/2 1,96 ,

 0,01 z/2 2,58 ,…) nên đôi khi kết quả kiểm định bác bỏ với mức ý nghĩa thứ nhất, nhưng lại chấp nhận với mức ý nghĩa thứ hai. Nên đôi khi các bài báo cáo sẽ chọn mức ý nghĩa thấp nhất để mô hình kiểm định có ý nghĩa.

Giá trị p hay mức ý nghĩa quan sát được là giá trị nhỏ nhất của  mà qua đó các mô hình kiểm

định có ý nghĩa về mặt thống kê

Nếu một kết quả kiểm định có ý nghĩa về mặt thống kê với  0,10 nhưng không có ý nghĩa với

 0,05 thì ta có thể hiểu giá trị p là một số trong khoảng 0,05 p 0,10 . Hay nói cách khác nếu giá trị p nhỏ hơn giá trị  , thì ta bác bỏ giả thiết H0và ngược lại.

6.2. KIỂM ĐỊNH GIẢ THIẾT CHO MỘT GIÁ TRỊ TỶ LỆ TỔNG THỂ.

6.2.1 Phân tích.

Xét một tổng thể và một đặc trưng A , mỗi phần tử trong tổng thể chỉ mang hai tính chất là có tính chất A hoặc không có tính chất A . Xét trên một mẫu dữ liệu cụ thể, ta cần kiểm định giả thiết tỷ lệ phần tử loại A trong tổng thể này là p , thì p có bằng giá trị p0cho trước hay không với mức ý nghĩa  .

Quan sát từng phần tử, coi phần tử quan sát có mang tính chất A hay không. Thực hiện công việc

n lần, tương ứng chính là mẫu dữ liệu. Gọi X là biến ngẫu nhiên chỉ số phần tử mang tính chất A

, kết hợp giả thiết p p0 ta có (theo chương 3 và 6) ta có:

np01p0

X ~ N np ,np 1 p z 

X np0

~ N 0;1

o 0 0

Đặt f là tỷ lệ phần tử mang tính chất A trong n phần tử quan sát. Ta có

z X np0

Xp

np0 1 p0 

n 0 

np0 1 p0 

n

f p0

p0 1 p0 

n ~ N 0;1

Giá trị z mang ý nghĩa đo mức chênh lệch giữa f (tỷ lệ phần tử mang tính chất A trên mẫu dữ liệu, đại diện cho p ) với p0.

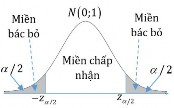
Trong bài toán kiểm định với giả thiết H0: p p0và đối thiết H1: p p0.

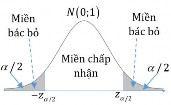
Mức ý nghĩa  được phân đều 2 phía và P z z/2  : là xác suất quyết định bác bỏ giả thiết H0khi thực tế giả thiết H0đúng.

Nghĩa là ta chấp nhận đối thiết H1 khi z z/2 hoặc

z z /2

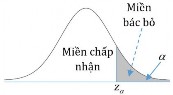
Trong bài toán kiểm định với giả thiết H0: p p0và đối thiết H1: p p0.

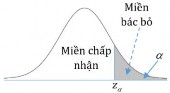
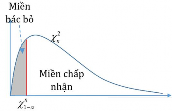
Mức ý nghĩa  được phân 1 phía phải và Pzz : là xác suất quyết định bác bỏ giả thiết H0khi thực tế giả thiết H0đúng.

Nghĩa là ta chấp nhận đối thiết H1 khi z z

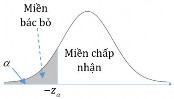
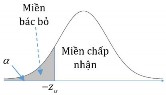
Trong bài toán kiểm định với giả thiết H0: p p0và đối thiết H1: p p0.

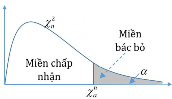
Mức ý nghĩa  được phân 1 phía phải và Pzz : là xác suất quyết định bác bỏ giả thiết H0khi thực tế giả thiết H0đúng.

Nghĩa là ta chấp nhận đối thiết H1 khi z z

1. Giả thiết không H0 : p p0

2. Giả thiết đối

3. Trị thống kê

Với f là tỷ lệ phần tử mang đặc trưng A của mẫu. Trị thống kê là : z 

4. Miền bác bỏ

6.2.2 Mô hình kiểm định.

Kiểm định hai phía

Kiểm định một phía
H1 : p p0	H1 : p p0 H1 : p p0

f p0 p0 1 p0 

n

Kiểm định 2 phía

Đối thiết : H1 : p p0

Bác bỏ H0 khi:

z z /2

zz z z/2

 /2

Kiểm định 1 phía Đối thiết : H1 : p p0 Bác bỏ H0 khi: z z /2

Kiểm định 1 phía Đối thiết : H1 : p p0 Bác bỏ H0 khi: z z

f p0 p0 1 p0 

n

Ví dụ 6.3 Các báo cáo trước đây khảo sát về gia cảnh của sinh viên năm nhất ở một trường đại học cho biết có 86% sinh viên đại học năm thứ nhất. Năm nay,trường đại học này làm một cuộc khảo sát tương tự về vấn đề trên, khi hỏi 1000 sinh viên năm thứ nhất được chọn ngẫu nhiên thì thấy có 890 sinh viên được nhận hỗ trợ tài chính từ gia đình. Với mức ý nghĩa  5% , các báo cáo trên có còn đúng cho tình hình sinh viên năm nay hay không.

Giải. Mô hình kiểm định trong trường hợp này có dạng

1.

H0 : p 86% và H1 : p 86%

Trong đó p là tỷ lệ sinh viên năm nhất nhận được hỗ trợ tài chính từ gia đình.

Và dữ liệu đề bài cho: n 1000 và f 890 0,89

2.

1000

Trị thống kê dùng trong mô hình này là z 

3.

Trong đó p0 0,86 nên ta có z 2,734

Mức ý nghĩa của kiểm định là 5% tương ứng phân vị z/2 1,96.

Kết luận : vì trị thống kê cao hơn phân vị zz/2 nên ta hoàn toàn có thể bác bỏ giả thiết H0, tức

tỷ lệ sinh viên năm nhất năm nay nhận được hỗ trợ tài chính từ gia đình khác với báo cáo các năm trước.

6.3. KIỂM ĐỊNH GIẢ THIẾT CHO MỘT TRUNG BÌNH TỔNG THỂ.

6.3.1 Phân tích.

Xét một tổng thể, gọi  là giá trị trung bình của tổng thể, dựa trên một mẫu cụ thể ta cần kiểm

định giả thiết trung bình tổng thể có bằng giá trị 0cho trước không với mức ý nghĩa  .

Gọi X là biến ngẫu nhiên chỉ giá trị của một phần tử trong tổng thể, giả sử X có quy luật phân phối chuẩn X ~ N ; 2,  2là phương sai tổng thể. Xét mẫu dữ liệu, có cỡ mẫu n và trung bình

của mẫu là X , (theo chương 5) ta có X ~ N ;  2 . Kết hợp giả thiết  

, đặt:

n 0



z X  X 0

2

n



n ~ N 0;1

Giá trị của z đo mức độ chênh lệch giữa trung bình mẫu (đại diện cho  ) và trong mô hình kiểm định giả thiết H0:  0.

0, là trị thống kê

Trong trường hợp phương sai tổng thể chưa biết, ta thay thế phương sai tổng thể bằng phương

n 1

n 1S 2

 2

sai mẫu S2. Đặt:

z X X . 1 X  .

X 

S

n

~ 

n 1S 2

S

n





n

X 

Trong đó

 ~ N 0;1và

2

 2 n1

nên z 

S

n ~ t n 1

n

Nhưng khi cỡ mẫu lớn hơn 30 thì phần phôi Student xấp xỉ bằng phân phối chuẩn. Nên khi phương

sai tổng thể chưa biết và cỡ mẫu n 30 , ta có:

z X 

S

n ~ N 0;1

Kiểm định hai phía	Kiểm định một phía
H1 :  0	H1 :  0 H1 :  0

6.3.2 So sánh trung bình tổng thể với một số khi biết phương sai.

1. Giả thiết không H0 :  0 .

2. Giả thiết đối.

3. Trị thống kê

Trị thống kê : z X0n



4. Miền bác bỏ

Kiểm định 2 phía Đối thiết : H1 :  0 Bác bỏ H0 khi: z z /2 z z  /2

Kiểm định 1 phía Đối thiết : H1 :  0 Bác bỏ H0 khi: z z

Kiểm định 1 phía Đối thiết : H1 :  0 Bác bỏ H0 khi: z z

1. Giả thiết không H0:  0.

2. Giả thiết đối.

3. Trị thống kê

Trị thống kê : z X0n

S

4. Miền bác bỏ

a. Trường hợp cỡ mẫu n 30 , trị thống kê có quy luật phân phối chuẩn : z~ N 0;1.

6.3.3 So sánh trung bình tổng thể với một số khi không biết phương sai.

Kiểm định hai phía

Kiểm định một phía
H1 :  0	H1 :  0 H1 :  0

S / n

Kiểm định 2 phía

Đối thiết : H1 :  0

Bác bỏ H0 khi:

z z /2

z z

 /2

Kiểm định 1 phía Đối thiết : H1 :  0 Bác bỏ H0 khi: z z	Kiểm định 1 phí Đối thiết : H1 :  0 Bác bỏ H0 khi: z z
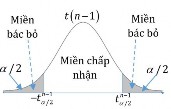
b. Trường hợp cỡ mẫu n 30 , trị thống kê có quy luật phân phối Student, bậc tự do n 1: z ~t n 1. Kiểm định 2 phía Kiểm định 1 phí Kiểm định 1 phía Đối thiết : H1 :  0 Đối thiết : H1 :  0 Đối thiết : H1 :  0 Bác bỏ H0 khi: Bác bỏ H0 khi: Bác bỏ H0 khi: z t n1 z tn1 z tn1  /2   z t n1  /2

Ví dụ 6.4 Sản lượng hàng ngày tại một nhà máy hóa chất, được ghi nhận cho n 50 ngày, có một số trung bình và độ lệch chuẩn của mẫu là X 871 tấn và S 21 tấn. Hãy kiểm định giả thuyết rằng sản lượng bình quân hàng ngày của nhà máy đó là  880 tấn mỗi ngày so với giả thuyết thay thế là  hoặc lớn hơn hay nhỏ hơn 880 tấn mỗi ngày.

Giải:

Mô hình kiểm định:

1. H0 :  880 tấn và H1 :  880 tấn

Với  là sản lượng trung bình của nhà máy hóa chất trong một ngày.

2. Trị thống kê : z X0

Trong đó X 871;  880; S 21;n 50 , vậy ta có z 3,03

3.

4.

Với  0.05 ; ta có z /2 1,96

Kết luận: vì z z/2 nên ta bác bỏ giả thiết H0; tức  880 tấn là sai.

Ví dụ 6.5 Khảo sát về việc đánh bắt các ngừ tại một vùng biển trong năm qua. Một báo cáo cho biết trọng lượng trung bình một con cá ngừ trong các năm trước là khoảng 30,31 pound

1pound 0.453592kg. Nhưng gần đây việc đánh bắt cá ngừ gia tăng, làm ảnh hưởng đến trọng

lượng trung bình của một con cá ngừ trong vùng, khảo sát mẫu gồm 20 con cho bảng số liệu sau:

17,4

18,9	39,6	34,4	19,6	24,1	39,6	12,2	25,5	22,1
33,7	37,2	43,4	41,7	27,5	29,3	21,1	23,8	43,2	24,4

Hỏi mẫu dữ liệu trên có đủ sức bác bỏ luận điểm trên hay không với mức ý nghĩa  5%

Giải. Mô hình kiểm định tương ứng bài toán là: 1. H0 :  30,31 và H1 :  30,31

Trong đó  là trọng lượng trung bình của 1 con cá ngừ bắt tại vùng biển này.

2. Trị thống kê của mô hình: (cỡ mẫu nhỏ n 20 ; phương sai tổng thể chưa biết) :

zX 0

S

n

Với các số liệu thu được ta có n 20 ; X 28,935 ; S 9,5074 . Nên ta có giá trị của trị thống kê:

z 0,6468 .

3.

4.

Với mức ý nghĩa  5% ta có phân vị sử dụng t n1 t192,093 .

 /2 0,025

Kết luận z t19 nên không đủ bằng chứng để bác bỏ giá thiết H , tức trọng lượng trung

0,025

bình của 1 con cá ngừ ở vùng biển này vẫn là 30,31 pound.

0

6.4. KIỂM ĐỊNH GIẢ THIẾT CHO PHƯƠNG SAI TỔNG THỂ.

6.4.1 Phân tích

0

Xét tổng thể, gọi  2là phương sai của tổng thể, dựa trên mẫu dữ liệu cụ thể, ta cần kiểm định giả thiết phương sai tổng thể có bằng giá trị  2cho trước hay không với mức ý nghĩa  .

Trong trường hợp, tổng thể biết giá trị trung bình là  và kết hợp giả thiết H : 2 2. Với mẫu

0 0

dữ liệu lần lượt nhận giá trị Xivới i 1,n , ta có



X ~ N , 2 Xi  ~ N 0;1với i 1,n .

i 0

0

Theo định nghĩa phân phối Chi bình phương ta có:

n

Xi 

2

 i 1 ~  2



2 n

0

Như vậy  là trị thống kê trong mô hình kiểm định giả thiết H : 2 2, với quy luật phân phối

0 0

Chi bình phương bậc tự do n .

Trong trường hợp, trung bình tổng thể chưa biết, với S 2 là phương sai mẫu dữ liệu, kết hợp giả

thiết H : 2  2 , trong Chương 5 ta có:

0 0

n 1S 2



 2

0

2

~ 

n1

Và ta có  lúc này là trị thống kê cho mô hình kiểm định H : 2 2, khi không biết trung bình

0 0

tổng thể, và có quy luật phân phối Chi bình phương bậc tự do n 1.

1.

2.

Giả thiết không H : 2 2 .

0

0

Giả thiết đối.

3. Trị thống kê.

6.4.2 So sánh phương sai tổng thể với một số khi biết trung bình µ.

Kiểm định hai phía

Kiểm định một phía
H : 2  2	H : 2  2
1 0	1 0
	H : 2  2
	1 0

Với  : trung bình tổng thể.

n

x  2

i

Trị thống kê :  i 1

 2

0

4. Miền bác bỏ.

Trị thống kê có quy luật phân phối Chi bình phương bậc tự do n :  ~  2

n

Kiểm định 2 phía Đối thiết : H : 2  2 1 0 Bác bỏ H0 khi:   n 1 /2   n  /2

Kiểm định 1 phí Đối thiết : H : 2  2 1 0 Bác bỏ H0 khi:  n 1

Kiểm định 1 phía Đối thiết : H : 2  2 1 0 Bác bỏ H0 khi:   n 

Kiểm định hai phía	Kiểm định một phía
H : 2  2	H : 2  2
1 0	1 0
	H : 2  2
	1 0

6.4.3 So sánh phương sai tổng thể với một số khi chưa biết trung bình µ.

1. Giả thiết không H : 2  2 .

0 0

2. Giả thiết đối.

3. Trị thống kê. Với

n 1S 2

Trị thống kê :  2

0

4. Miền bác bỏ.

Trị thống kê có quy luật phân phối Chi bình phương bậc tự do n1:  ~ 2

n1

Kiểm định 2 phía Đối thiết : H : 2  2 1 0 Bác bỏ H0 khi:   n1 1 /2   n1  /2

Kiểm định 1 phía Đối thiết : H : 2  2 1 0 Bác bỏ H0 khi:  n1 1

Kiểm định 1 phía Đối thiết : H : 2  2 1 0 Bác bỏ H0 khi:  n1 