Kiểm Định Giả Thiết Cho Hai Phương Sai Tổng Thể

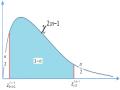
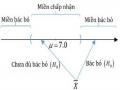
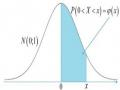
6.7. KIỂM ĐỊNH GIẢ THIẾT CHO HAI PHƯƠNG SAI TỔNG THỂ

Kiểm định hai phía	Kiểm định một phía
H : 2  2 1 1 2	H : 2  2 1 1 2 H : 2  2 1 1 2

Có thể bạn quan tâm!

• Khoảng Tin Cậy Cho Độ Lệch Hai Giá Trị Tỷ Lệ.
• Kiểm Định Giả Thiết Cho Một Giá Trị Tỷ Lệ Tổng Thể.
• Kiểm Định Giả Thiết Cho Hai Giá Trị Tỷ Lệ Tổng Thể.
• Thống kê ứng dụng trong kinh tế và kinh doanh - Trường ĐH Văn Lang - 16
• Thống kê ứng dụng trong kinh tế và kinh doanh - Trường ĐH Văn Lang - 17

Xem toàn bộ 142 trang tài liệu này.

Khi cần có một phương pháp để thực hiện kiểm định 2 tổng thể có biến động cùng mức độ như nhau hay không (ví dụ tính ổn định của phương pháp sản xuất, cách cho điểm của 2 giảng viên đại học…) chúng ta dùng phương pháp kiểm định phương sai của hai tổng thể độc lập:

1. Giả thiết không H : 2  2 .

0 1 2

2. Giả thiết đối.

3. Trị thống kê.

Với S1; S2: độ lệch chuẩn của mẫu thứ nhất và mẫu thứ hai với cỡ mẫu lần lượt là n1;n2

S 2

Trị thống kê : F  1

S 2

2

4. Miền bác bỏ.

Trị thống kê có quy luật phân phối Fisher bậc tự do n ;n : F ~ F n11,n21

1 2 

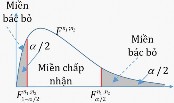
Kiểm định 2 phía Đối thiết : H : 2  2 1 1 2 Bác bỏ H0 khi: F  n1 ;n2 1 /2 F  n1 ;n2  /2

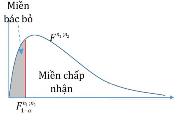
Kiểm định 1 phía Đối thiết : H : 2  2 1 1 2 Bác bỏ H0 khi: n1;n2 1

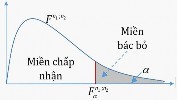
Kiểm định 1 phía Đối thiết : H : 2  2 1 1 2 Bác bỏ H0 khi:   n1 ;n2 

6.8. KIỂM TRA GIẢ THIẾT VỀ SỰ ĐỘC LẬP

6.8.1 Phân tích.

Xét một tổng thể trên đó có hai dấu hiệu định tính X;Y . Giả sử thuộc tính X có k trường hợp là

x1 ; x2 ;...; xk

, và thuộc tính Y có m trường hợp là

y1 ; y2 ;...; ym . Khảo sát một bộ mẫu gồm n dữ

liệu, bảng tần số tương ứng với từng cặp trường hợp của 2 thuộc tính X;Y có dạng:

X Y

y1	y2	…	y j	…	ym	Tổng cột
x1	n11	n12	…	n1 j	…	n1m	p1
x2	n21	..	…	n2 j	…	n2m	p2
…	…	…	…	…	…	…	…
xi	ni 1	ni 2	…	nij	…	nim	pi
…	…	…	…	…	…	…	…
xk	nk 1	nk 2	...	nkj	…	nkm	pk
Tổng hàng	q1	q2	…	qj	…	qm	n

m

Trong đó pinij

j 1

k

và qjnij

i 1

Giả thiết H0 đặt ra là hai thuộc tính X;Y là độc lập với nhau. Theo giả thiết đó ta có

P X xi Y y j P X x i .P Y y j 

Và tương đương với nij pi . qj

n n n

với mọi i 1,k ; j 1,m.

Vì thế trị thống kê cho mô hình kiểm định giả thiết H0là:

k m n n n 

nij pi . qj 

G n~  2

i 1 j 1pi. qj

k 1m1

n n

Rút gọn biểu thức G ta có công thức tính trị thống kê:

k m n2 

G n ij 1

i 1 j 1 pi .qj 

6.8.2 Kiểm định độc lập của hai bộ dữ liệu định tính.

1. Giả thiết không H0 : X;Y độc lập với nhau.

2. Giả thiết đối H1 : X ;Y không độc lập với nhau.

3. Trị thống kê

Với nij : chỉ số phần tử mà thuộc tính X nhận giá trị xivà thuộc tính Y nhận

giá trị y jvới i 1, k và j 1,m .

pi: chỉ số phần tử mà thuộc tính X nhận giá trị xi.

qj: chỉ số phần tử mà thuộc tính Y nhận giá trị y j.

k m n2 

Trị thống kê : G n ij 1

i 1 j 1 pi .qj 

4. Miền bác bỏ

Trị thống kê có quy luật phân phối Chi bình phương, bậc tự do s k 1m1:

G ~  2 .

k1m1

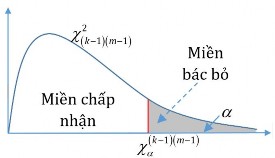
Đối thiết H1 : X;Y không độc lập với nhau. Bác bỏ H khi: G  k1m1 0 

Ví dụ 6.12 Một hãng bánh muốn khảo sát về sự ảnh hưởng của màu sắc đối với các loại bánh được khách hàng chọn mua. Một mẫu gồm 148 chiếc bánh được bán ra có kết quả như sau

Bánh đậu	Bánh dừa	Bánh thập cẩm
Màu tự nhiên	20	25	18

Mô hình kiểm định

1.

2.

H0 : Màu sắc và loại bánh độc lập với nhau.

H1 : Màu sắc và loại bánh phụ thuộc vào nhau.Trị thống kê :

G 14849.63 68.63 31.63 49.85 68.85 31.85 4,0552

202 252 182 292 432 132







3. Với mức ý nghĩa 5% ta có phân vị của phân phối Chi bình phương bậc tự do 2131

là 3 5,991

0,05

4.

Kết luận : Vì G 3 nên chấp nhận giả thiết H nghĩa bánh được mua, giữa loại bánh và

0,05

màu sắc là độc lập với nhau.

0

Phẩm màu

29

43

13

Với mức ý nghĩa  5% , kiểm định bánh được chọn mua có ảnh hưởng bởi màu sắc không.

Bánh đậu	Bánh dừa	Bánh thập cẩm	Tổng cột
Màu tự nhiên	20	25	18	63
Phẩm màu	29	43	13	85
Tổng dòng	49	68	31	148

CHƯƠNG 7

F

Mục lục chương 7

7.1 Chuỗi thời gian, các khái niệm cơ bản 109

7.2 Các phương pháp dự báo đơn giản 106

7.3 Các phương pháp làm trơn 108

7.1 CHUỖI THỜI GIAN, CÁC KHÁI NIỆM CƠ BẢN

7.1.1 Khái niệm chuỗi thời gian.

Chuỗi thời gian là tập hợp các dữ liệu có sự phụ thuộc của các giá trị quan sát được thu thập qua thời gian. Với mục tiêu là dùng các dữ liệu trong quá khứ để phân tích và dự báo cho dữ liệu trong tương lai.

t	t1	t2	…	tn
Y	Y1	Y2	…	Yn

Biểu diễn cho dữ liệu được sắp xếp theo thứ tự thời gian, dạng tổng quát như sau

Trong đó : ti

là thời gian thứ i và Yilà giá trị lượng biếnquan sát được ở thời gian ti. i 1;n

Căn cứ vào đặc điểm biến động về quy mô của hiện tượng thời gian, chuỗi thời gian được chia ra

làm hai trường hợp

Chuỗi thời kỳ : biểu hiện giá trị lượng biến quan sát thu được trong từng khoảng thời gian nhất định. Các giá trị của lượng biến có thế cộng dồn với nhau tạo thành giá trị của lượng biến trong khoảng thời gian dài hơn.

Ví dụ 7.1 Sản lượng xuất khẩu cà phê của Việt Nam từ 2001 đến 2005:

Năm

2001	2002	2003	2004	2005
Sản lượng (ngàn tấn)	931,1	722,2	794,4	976,2	892,4

Chuỗi thời điểm : biểu hiện giá trị lượng biến quan sát tại các thời điểm quan sát nhất định, và giá trị của lượng biến khi cộng dồn thì không có ý nghĩa.

Ví dụ 7.2 Giá vàng SJC tại TPHCM trong tuần cuối tháng 7 năm 2017:

Ngày

23/7	24/7	25/7	26/7	27/7	28/7
Ngàn đồng/chỉ	1317,0	1316,5	1310,0	1307,5	1294,0	1294,0

Các phương pháp dự báo chuỗi thời gian được chia thành hai loại:

Phương pháp dự báo, tính toán cho các giá trị tương lai dựa trên toàn bộ các quan sát có

được trong quá khứ.

Phương pháp dự báo dựa trên nguyên nhân kết quả của các dữ liệu.

7.1.2 Các thành phần chuỗi thời gian.

i. Thành phần xu hướng.

Thành phần xu hướng là thành phần thể hiện mức tăng giảm của lượng biến quan sát theo một quy luật nào đó trong một khoảng thời gian đủ dài. Nguyên nhân của thành phần xu hướng là do những thay đổi về dân số, thay đổi về xã hội, thay đổi về công nghệ, thay đổi về nhu cầu, sở thích…

ii. Thành phần chu kỳ.

Mặc dù chuỗi thời gian có thể biểu hiện tính xu hướng qua thời kỳ dài, nhưng không phải tất cả các giá trị lượng biến sẽ quan sát trong tương lai sẽ nằm trên đường xu hướng. Thực tế dữ liệu khi quan sát trong một khoảng thời gian dài với tần suất tính bằng năm thì ta nhận ra có sự thay đổi luân phiên lên xuống của lượng biến xung quanh đường xu hướng, nguyên nhân là do thành phần chu kỳ trong chuỗi thời gian.

iii. Thành phần mùa.

Trong khi thành phần xu hướng và thành phần chu lỳ của chuỗi thời gian được xác định bằng cách phân tích chuỗi thời gian kéo dài qua nhiều năm, thì nhiều chuỗi thời gian cho thấy có những kiểu biến thiên lặp lại theo tần suất theo quý , theo mùa,…, biến động của lượng biến tuân theo một quy luật nào đó giữa các thời điểm trong năm và lặp lại trong các năm kế tiếp

iv. Thành phần bất thường.

Ngoài các yếu tố xu hướng , chu kỳ, và mùa, thực tế giá trị lượng biến quan sát còn chịu sự chi phối của các yếu tố ngẫu nhiên, các yếu tố bất thường ngắn hạn không chịu sự liên kết với thành phần khác như mùa, chu kỳ, xu thế.

Ví dụ 7.3 Cho bảng số liệu về số lượng tủ lạnh một chuỗi siêu thị điện máy bán trong 8 năm, số

liệu khảo sát theo từng quý (đơn vị : ngàn cái).

Q1-2005

Q2-2005	Q3-2005	Q4-2005	Q1-2006	Q2-2006	Q3-2006	Q4-2006	Q1-2007
1317	1615	1662	1295	1271	1555	1639	1238	1277
Q2-2007	Q3-2007	Q4-2007	Q1-2008	Q2-2008	Q3-2008	Q4-2008	Q1-2009	Q2-2009
1258	1417	1185	1196	1410	1417	919	943	1175
Q3-2009	Q4-2009	Q1-2010	Q2-2010	Q3-2010	Q4-2010	Q1-2011	Q2-2011	Q3-2011
1269	973	1102	1344	1641	1225	1429	1699	1749
Q4-2011	Q1-2012	Q2-2012	Q3-2012	Q4-2012
1117	1242	1684	1764	1328

1800

1700

1600

1500

1400 Q

1300

1200

1100

1000

900

800

0

Q3-2011 Q3-2012

Q3-2005

Q

2-2005

Q

5

10

15

20

25

30

35

Q3-2006

Q

Q3-2010

2-2011

Q2-

2012

2-2006

Q

3-2007Q2Q-230-02

8008

Q1-

Q2-2010

2011

1-2005Q4-Q210-0

25006 Q1Q-220-02

Q

4-2006

7007

Q3-200

9

Q4-2012

2

Q4Q-210-027008

Q2-2009

Q4-201

0

Q1-201

Q

1-2010

Q4-2011

4Q-210-02800 Q4-

9

2009

Q

Biểu đồ trên cho thấy số lượng tủ lạnh bán được tăng giảm đều đặn, điều này thể hiện biến động theo mùa, cụ thể trong 1 năm số lượng tủ lạnh tăng mạnh từ quý 1 lên quý 2 và giảm mạnh từ quý 3 xuống quý 4.

7.1.3 Các đại lượng mô tả chuỗi thời gian.

i. Mức độ trung bình theo thời gian

Trung bình chuỗi thời gian, đối với chuỗi thời kỳ.

Y 

1

n

Y1Y2... Yni 1

Yi

n

n

Trong đó : Y : mức độ trung bình của chuỗi.

Yi: Giá trị lượng biến chuỗi thời kỳ

Trung bình chuỗi thời gian, đối với chuỗi thời điểm, khoảng cách giữa thời điểm bằng nhau:

Y 

n 1 2

1

Y

1 2 2 3

Y Y Y





2

... Y

n1 n

2

Y









1

n 1 2

1Y Y ... 1 Y 





1 2

2

n





Trong đó : Y : mức độ trung bình của chuỗi.

Yi: Giá trị lượng biến chuỗi thời kỳ

Ví dụ 7.4 Khảo sát lượng lao động của một doanh nghiệp tại các thời điểm thu được bảng số liệu

sau:

Ngày

15/5/2018	15/6/2018	15/7/2018	15/8/2018
Số lao động	350	370	370	380

Giữa hai thời điểm giữa tháng 5 và 6, ta có số lao động trung bình là Y1 Y2 350 370

2 2

Tương tự cho các khoảng thời gian còn lại.

Vậy trung bình lượng lao động trong khoảng thời gian 3 tháng là:

Y 1 350 370 370 370 370 380 368,33

3 2 2 2 



Vậy trung bình doanh nghiệp này có bình quân 369 lao động từ 15/5 đến 15/8.

Trung bình chuỗi thời gian, đối với chuỗi thời điểm, khoảng cách giữa thời điểm không bằng nhau:

Y 1 1 2 2 n ni 1

Y t Y t ... Y t

n

Yi ti

t1 t2 ... tn



n

t

i

i 1

Trong đó : Y : mức độ trung bình của chuỗi.

Yi: Giá trị lượng biến chuỗi thời kỳ

ti : độ dài thời gian tương ứng mức độ thứ i .

Ví dụ 7.5 Ghi nhận về số lao động, ghi nhận trong tháng 5 thay đổi như sau

Ngày

1/5/2018	10/5/2018	15/5/2018	21/5/2018
Số lao động	380	385	388	384

Đầu tháng 5 : có 380 lao động. Ngày 10/5 nhận thêm 5 lao động, tối 15/5 nhận thêm 3 lao động. Ngày 21/5 sa thải 4 lao động, và giữ nguyên cho đến 30/5.

Ngày

Số lao động

Khoảng thời gian

Yiti

1

380	9	3420
10	385	5	1925
15	388	6	2328
21	384	10	3840
30	384	ti30	tiYi11513

n

Yi ti

11513

30

Vậy số lao động trung bình trong tháng là : Y i 1383,77 (người)

ii. Lượng tăng giảm tuyệt đối.

n

ti i 1

Lượng tăng giảm tuyệt đối liên hoàn: thể hiện mức chênh lệch tuyệt đối của lượng biến quan sát

ở hai mốc thời gian liên tiếp nhau.

iYiYi1 i 2,n

Lượng tăng giảm tuyệt đối định gốc: thể hiện mức chênh lệch tuyệt đối giữa lượng biến ở mốc thời gian bất kỳ so với lượng biến quan sát chọn làm gốc (thường được chọn là lượng biến quan sát đầu tiên)

i Yi Y1 i 2, n

Lượng tăng giảm tuyệt đối trung bình: là trung bình cộng các lượng tăng giảm tuyệt đối liên hoàn qua tất cả các mốc thời gian.

 

1

n 1



n

 

i

1

n 1



Y Y Y Y ... Y Y

2 1 3 2

n n1

Yn Y1

i 2

n 1

Lưu ý : đại lượng này chỉ có ý nghĩa thống kê khi lượng tăng (giảm) tuyệt đối liên hoàn xấp xỉ nhau, nếu không vô tình lượng tăng giảm tuyệt đối sẽ đánh giá sai nguyên nhân gây ra sự biến động của chuỗi thời gian.

iii. Tốc độ phát triển.

Tốc độ phát triển liên hoàn: thể hiện tốc độ thay đổi của 2 lượng biến quan sát ở hai mốc thời gian

liên tiếp nhau.

t 

Y

i

i

Y

i 2,n

i 1

Tốc độ phát triển định gốc : thể hiện tốc độ thay đổi của lượng biến ở mốc thời gian bất kỳ so với

lượng biến quan sát chọn làm gốc (thường được chọn là lượng biến quan sát đầu tiên)

T 

Y

i

i

Y

i 2, n

1

Tốc độ phát triển trung bình : thể hiện nhịp độ phát triển bình quân giữa 2 lượng biến quan sát liên tiếp nhau trong suốt thời gian, được tính bằng trung bình nhân của tất cả tốc độ phát triển

liên hoàn.

t n1

n



i 2

ti n1 . ... n1

Y2 Y3

Yn

Y1 Y2

Yn1

Yn Y1

Lưu ý : Cũng giống như lượng tăng giảm tuyệt đối trung bình, tốc độ phát triển trung bình chỉ mang ý nghĩa khi các tốc độ phát triển liên hoàn xấp xỉ nhau trong suốt thời kỳ nghiên cứu.

iv. Tốc độ tăng giảm.

Tốc độ tăng giảm liên hoàn : đánh giá tốc độ thay đổi tương đối của 2 lượng biến quan sát ở hai

mốc thời gian liên tiếp nhau.

a 

Y Y

i i 1

Y

t 1 i 2,n 



i

i

i

i 1 i 1

Y

Tốc độ tăng giảm định gốc : đánh giá tốc độ thay đổi tương đối của một lượng biến ở một mốc thời gian bất kỳ so với lượng biến quan sát chọn làm gốc (thường được chọn là lượng biến quan sát

đầu tiên)

A Yi Y1 i T 1 i 2,n

i

Y Y

i

1

i

Tốc độ tăng giảm trung bình :

a t 1

Ví dụ 7.6 Cho doanh thu của một công ty qua các năm (từ 2012 đến 2017) theo bảng số liệu dưới đây.:

Chỉ tiêu

2011	2012	2013	2014	2015	2016	2017
1. Doanh thu (tỷ VNĐ)	50
2. Lượng tăng tuyệt đối liên hoàn (tỷ VNĐ)		25					20
3.Tốc độ phát triển liên hoàn (%)				115		125
4.Tốc độ tăng giảm liên hoàn (%)			10
5. Giá trị tuyệt đối của 1% của tốc độ tăng (tỷ VNĐ)						0,98

Chỉ tiêu

2011	2012	2013	2014	2015	2016	2017
1. Doanh thu (tỷ VNĐ)	50	75	82,5	94,875	98	122,5	142,5
2. Lượng tăng tuyệt đối liên hoàn (tỷ VNĐ)		25					20
3.Tốc độ phát triển liên hoàn (%)				115		125
4.Tốc độ tăng giảm liên hoàn (%)			10
5. Giá trị tuyệt đối của 1% của tốc độ tăng (tỷ VNĐ)						0,98

7.2 CÁC PHƯƠNG PHÁP DỰ BÁO ĐƠN GIẢN

7.2.1 Dự báo bằng lượng tăng (giảm) tuyệt đối.

Phương pháp thường dụng khi dãy lượng biến theo thời gian có biến động ít, nghĩa là lượng tăng

(giảm) tuyệt đối liên hoàn xấp xỉ nhau.

YnL Yn .L

Trong đó : YnL : là giá trị dự báo tại thời điểm n L .

Yn: là giá trị quan sát tại thời điểm thứ n (thời điểm cuối)

 : là lượng tăng giảm tuyệt đối trung bình.

L : tầm xa dự đoán.