Biện Pháp 2: Xây Dựng Bài Toán Hình Học Kết Thúc Mở Hỗ Trợ Hs Phát Triển

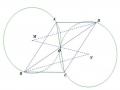
HS quan sát và phát hiện ra tính chất khi kéo rê điểm C tùy ý trên mặt phẳng và nhận thấy trung điểm G của DE vẫn không di chuyển. Vị trí chôn kho báu là điểm cố định G mà đường thẳng DE luôn đi qua G (Hình 2.2).

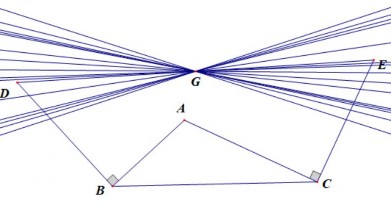
Hình 2.2

Bước 3: Đề xuất giả thuyết ngoại suy

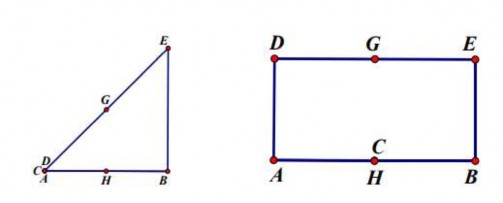
Quan sát biểu diễn trong trường hợp C trùng với A (Hình 2.3a), C trùng với B, hay C trùng với trung điểm H của AB (Hình 2.3b), các em đưa ra giả thuyết ngoại suy:

Hình 2.3a Hình 2.3b

Có thể bạn quan tâm!

Xem toàn bộ 143 trang tài liệu này.

“Khi C thay đổi thì G nằm trên trung trực của AB và HG HA HB ”

Bước 4: Kiểm chứng giả thuyết nhờ suy luận quy nạp và sử dụng BDTQ động

Để xác định được tính đúng đắn của giả thuyết GV hướng dẫn kéo rê ngẫu nhiên kết hợp với việc sử dụng các công cụ đo đạc, tính toán của phần mềm và suy luận thấy rằng khi C thay đổi thì G nằm trên trung trực của AB và HG HA HB.

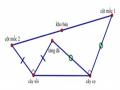
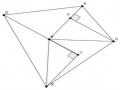
Ví dụ 2.2: Cho tứ giác ABCD. Về phía ngoài của tứ giác dựng các hình vuông nhận AB, BC, CD, DA tương ứng làm cạnh của nó. Gọi M, N, P, Q lần lượt là tâm của các hình vuông này. Trong trường hợp tổng quát, có nhận xét gì về tứ giác.

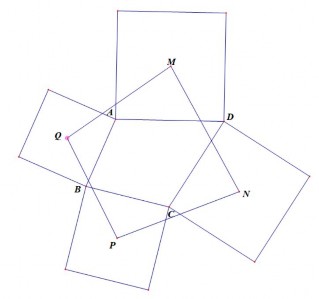
Hình 2.4

Bài tập này HS chưa xác định được kết luận cần chứng minh mà HS phải đi tìm kết luận đó. Dạng bài tập này là một dạng khá phức tạp đối với HS. GV sử dụng phần mềm toán học động GeoGebra như sau:

Bước 1: Khám phá ngẫu nhiên

Để HS phát hiện được kết quả bài toán GV sử dụng phần mềm hình học động kéo rê xem các đỉnh A, B, C, D một cách tùy ý. HS chú ý quan sát tìm ra các tính chất của tứ giác MNPQ. HS sẽ nhận thấy tứ giác MNPQ có rất nhiều hình dạng và chưa đưa ra được một đặc điểm đặc biệt nào của tứ giác MNPQ. GV có thể gợi ý HS chú ý vào các đường chéo của tứ giác MNPQ.

Bước 2: Phát hiện bất biến

HS quan sát và phát hiện ra tính chất của hai đường chéo của tứ giác MNPQ “Hai đường chéo vuông góc với nhau và bằng nhau” và “giao điểm của AC và BD trùng với giao điểm của MP và NQ”.

Bước 3: Đề xuất giả thuyết ngoại suy

HS đưa ra các giả thuyết “ Hai đường chéo vuông góc với nhau”, “giao điểm của AC và BD trùng với giao điểm của MP và NQ”, “MP và NQ luôn bằng nhau” . HS đưa ra 3 giả thuyết và ba giả thuyết này có cấu trúc ngoại suy như sau:

D: ? C: MPNQ D: ? C: MP=NQ

W: ? W: ?

D: ? C: MPNQ ACBD

W: ?

Đây đều là các ngoại suy sáng tạo. HS phải đi tìm kiếm các dữ liệu để kiểm chứng các giả thuyết của mình.

Bước 4: Kiểm chứng giả thuyết nhờ suy luận quy nạp và sử dụng BDTQ động

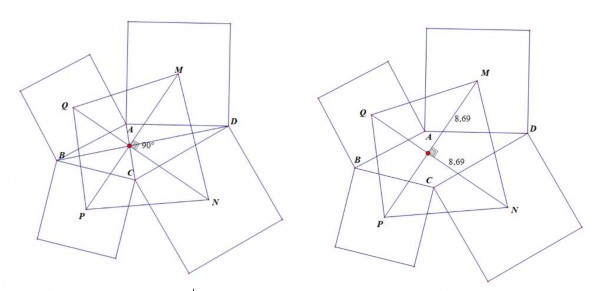
Hình 2.5

Để xác định được tính đúng đắn của giả thuyết GV hướng dẫn kéo rê ngẫu nhiên kết hợp với việc sử dụng các công cụ đo đạc, tính toán của phần mềm và nhận thấy “Hai đường chéo vuông góc với nhau”, “MP và NQ luôn bằng nhau” khi tứ giác MNPQ có các hình dạng khác nhau, lập tức bác bỏ giả thuyết “giao điểm của AC và BD trùng với giao điểm của MP và NQ” khi kéo rê. HS dẫn đến kết luận “Tứ giác MNPQ có hai

đường chéo vuông góc và có độ dài bằng nhau”.

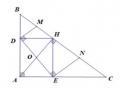
Ví dụ 2.3: Cho đường (O) trên đường tròn đó lấy hai điểm cố định B, C và điểm A di

động. Tìm quỹ tích trực tâm H của tam giác ABC khi A thay đổi trên đường tròn.

Bước 1: Khám phá ngẫu nhiên

GV kéo rê điểm A về các vị trí đặc biệt yêu cầu HS quan sát. HS sẽ nhận thấy điểm A đối xứng với C qua tâm O thì điểm H trùng với điểm B, điểm A đối xứng với điểm B qua tâm O thì điểm H trùng với điểm C (Hình 2.4).

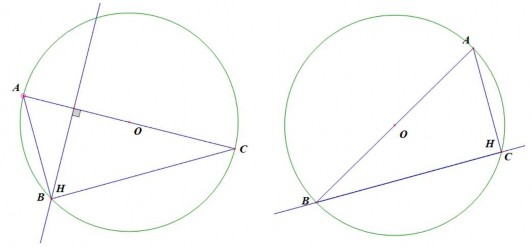
Hình 2.6

Bước 2: Phát hiện bất biến

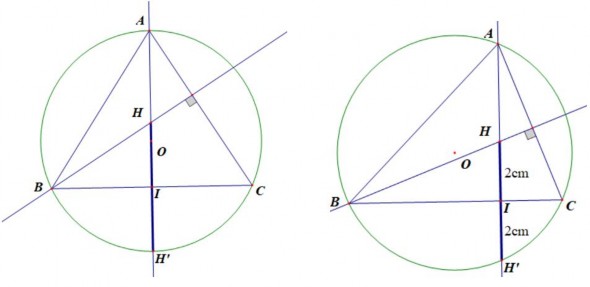
Hình 2.7

HS nhận thấy điểm B, C đều nằm trên đường tròn tâm O. GV kéo A đến vị trí chính giữa của cung BC thì HS nhận thấy H không nằm trên đường thẳng BC, H nằm

trên đường kính, HS nhận thấy IH=IH’. HS kéo điểm A đi vị trí khác và HS cǜng nhận thấy IH=IH’ với H’ là giao điểm của của AH và (O), I là giao điểm của AH với dây cung BC.

Bước 3: Đề xuất giả thuyết bằng suy luận ngoại suy

Từ những phát hiện trên HS đưa ra giả thuyết ngoại suy “Tập hợp điểm H nằm trên một đường tròn có cùng bán kính với đường tròn tâm O”

D: ? C: Tập hợp điểm H nằm trên một đường tròn

W: ?

HS cần đi tìm kiếm dữ liệu để giải thích kết luận trên.

Bước 4: Kiểm chứng giả thuyết nhờ suy luận quy nạp và sử dụng BDTQ động

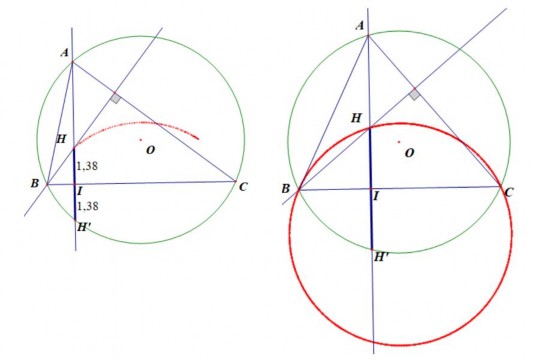
Hình 2.8

GV giúp HS kiểm chứng lại giả thuyết bằng phần mềm bằng cách cho phần mềm chạy tìm quỹ tích của điểm H (Hình 2.6).

2.2.2. Biện pháp 2: Xây dựng bài toán hình học kết thúc mở hỗ trợ HS phát triển khả năng khám phá toán bằng suy luận thông qua việc sử dụng BDTQ.

a) Cơ sở của biện pháp

Bài toán kết thúc mở (KTM) là bài toán có nhiều câu trả lời đúng và nhiều phương án giải khác nhau để đi đến các câu trả lời này (Becker & Shimada, 1997, [12]). Từ khoảng những năm 70 cho đến nay, những hoạt động khảo sát với các bài toán KTM trong giáo dục toán được phát triển mạnh mẽ cả về bề rộng lẫn chiều sâu. Khởi đầu là chuỗi các dự án nghiên cứu phát triển trong 6 năm (từ 1971-1976) của các nhà nghiên cứu giáo dục toán ở Nhật nhằm đánh giá tư duy bậc cao của HS khi làm việc với các bài toán KTM. Sau đó, ý tưởng sử dụng các bài toán KTM để phát triển các chiến lược giải quyết vấn đề và các kĩ năng tư duy bậc cao được lan rộng đến chương trình học của nhiều nước trên thế giới. Điều làm cho các bài toán KTM trở thành một tiếp cận hấp dẫn đối với dạy học toán là bởi bản chất “mở” của nó thách thức tư duy của người học.

Theo Mogetta, một bài toán hình học kết thúc mở được nhận ra bởi các đặc điểm sau [30]:

- Phát biểu bài toán thường chỉ là những mô tả rất ngắn gọn về các bước dựng hình theo trình tự và không đề nghị bất cứ một phương pháp giải cụ thể nào.

- Khác với dạng câu hỏi đóng truyền thống như “Chứng minh rằng…”, các bài toán hình học kết thúc mở thường yêu cầu HS tự đề xuất giả thuyết. Các câu hỏi của bài toán thường được diễn đạt dưới dạng: “Em tìm thấy mối quan hệ nào giữa…”, “Trong điều kiện nào thì…?”, “Hình … có thể trở thành những hình dạng nào…?”.

- Trong khi các bài toán truyền thống yêu cầu HS chứng minh một kết quả đúng đã được khẳng định từ trước, các bài toán hình học kết thúc mở chứa đựng yếu tố mở theo quan điểm khuyến khích suy nghĩ “phân kì” của HS. HS được tự do khám phá và suy luận để đưa ra nhiều giả thuyết khác nhau, đánh giá chúng để chọn một giả thuyết tốt nhất trước khi tìm kiếm con đường chứng minh. Do đó, ngay cả khi bài toán được xem là chỉ có một câu trả lời đúng, nó cǜng đem lại một hướng tiếp cận “mở” cho HS ngay từ đầu qua việc tạo điều kiện cho các em thoải mái thể hiện năng lực toán học ở các mức độ khác nhau tùy theo trình độ của từng cá nhân. Cấu trúc của các câu hỏi

trong bài toán kết thúc mở cǜng ủng hộ HS khảo sát tất cả các tùy chọn có thể xảy ra cho một câu trả lời, chẳng hạn: “Trong điều kiện… thì hình… trở thành…”, “Hình… có thể trở thành những hình dạng…”.

Ngoài ra, trong môi trường toán học với sự có mặt của các phần mềm hình học động như Cabri, GSP…,khả năng suy luận của HS có thể được hỗ trợ mạnh mẽ bởi:

- Khả năng kiểm chứng một dự đoán thông qua một số lượng lớn các ví dụ và việc thực hiện lặp lại các thử nghiệm, dựa trên các phản hồi nhanh chóng và chính xác được hỗ trợ bởi máy tính và công nghệ.

- Khả năng điều chỉnh linh hoạt một số điều kiện ban đầu của bài toán để đi đến những khảo sát mới với những giả thuyết mới, hay đi đến các kết quả tổng quát.

Bài toán kết thúc mở giúp HS được tự do khám phá và suy luận để đưa ra nhiều giả thuyết khác nhau, đánh giá chúng để chọn một giả thuyết tốt nhất trước khi tìm kiếm con đường chứng minh.

Biện pháp này giúp HS phát triển khả năng quan sát những biểu diễn trực quan đưa ra những giả thuyết mới và tiến hành tổng quát hóa, khả năng xác định căn cứ ở mỗi bước lập luận của HS, khả năng chuyển từ suy luận sang chứng minh hình học.

b) Cách thức thực hiện biện pháp

Để tìm hiểu về cách thức thực hiện biện pháp, ta xét các ví dụ dưới đây:

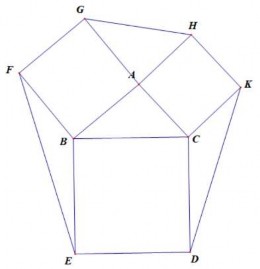
Ví dụ 2.4: Trên trang trắng của màn hình GSP, GV dựng tam giác ABC bất kì và ba hình vuông ABFG, BCDE và ACKH trên ba cạnh AB, BC và AC của tam giác ABC (Hình 2.9). Yêu cầu đối với HS:

(i) Đề xuất các mối quan hệ có thể giữa các tam giác BEF, CDK, AGH?

(ii) Chứng minh các kết quả được đề xuất.

Hình 2.9. BDTQ minh họa ví dụ 2.4

Trước khi dạng bài toán KTM này được đưa ra cho HS, GV cần giúp các em hiểu thế nào là mối quan hệ giữa các hình hình học. Chẳng hạn, khi xem xét mối quan hệ giữa các tam giác trong hình học phẳng, HS có thể liên tưởng đến sự bằng nhau, đồng dạng, hay tam giác này là ảnh của tam giác kia qua phép vị tự, tịnh tiến, phép quay…, các mối quan hệ liên quan đến chu vi, diện tích tam giác.

Trên trang hình GSP, khi thực hiện kéo rê ngẫu nhiên các đỉnh A, B, C đến các vị trí khác nhau và quan sát, HS có thể loại bỏ ngay giả thuyết các tam giác BEF, CDK, AGH bằng nhau hay đồng dạng. HS tiếp tục thao tác trên BDTQ của bài toán và luân phiên sử dụng suy luận ngoại suy, quy nạp cùng với các công cụ trợ giúp của phần mềm GSP để khám phá những mối quan hệ khác giữa các tam giác BEF, CDK, AGH. Chẳng hạn, khi thực hiện kéo rê về các trường hợp đặc biệt đối với đỉnh A sao cho tam giác ABC đều và quan sát thấy các tam giác BEF, CDK, AGH ở các vị trí bằng nhau, HS có thể nghĩ đến giả thuyết suy luận: “Diện tích các tam giác BEF, CDK, AGH bằng nhau” (Hình 2.10a). Để kiểm chứng giả thuyết bằng thực nghiệm, HS thực hiện kéo rê ngẫu nhiên đỉnh A để đưa tam giác ABC về các hình dạng tùy ý và sử dụng công cụ tính diện tích tam giác của GSP để quan sát. Tương tự, khi thực hiện kéo rê về các trường hợp đặc biệt đối với đỉnh A sao cho tam giác ABC vuông tại B và quan sát thấy các tam giác BEF, ABC ở các vị trí bằng nhau, HS đưa ra giả thuyết: “Diện tích tam giác BEF bằng diện tích tam giác ABC” (Hình 2.10b). Giả thuyết tiếp tục được kiểm chứng và khẳng định bằng kéo rê ngẫu nhiên đỉnh A và sử dụng công cụ tính diện tích tam giác của GSP. Do đó, HS đi đến một giả thuyết tổng quát hơn: “Diện tích các tam giác BEF, CDK, AGH không chỉ bằng nhau mà còn bằng diện tích tam giác ABC”. HS tiến hành kiểm chứng giả thuyết này bằng cách kéo rê ngẫu nhiên các điểm A, B, C cho di chuyển tự do trong mặt phẳng và sử dụng công cụ tính diện tích của GSP đối với các tam giác ABC, BEF, CDK, AGH để có các số liệu minh chứng.

Cuối cùng, năng lực suy luận giúp HS tìm ra con đường chứng minh. Chẳng hạn để chứng minh hai tam giác ABC và BEF có diện tích bằng nhau, HS có thể chọn chứng minh các chiều cao tương ứng AI, FJ bằng nhau (do đáy BC, BE của hai tam giác này bằng nhau). Và AI = FJ là do chúng là hai cạnh tương ứng của hai tam giác bằng nhau ABI và BFJ (Hình 2.10c).