Biện Pháp 3: Phát Triển Khả Năng Tư Duy, Dự Đoán Phát Hiện, Định Hướng Lời

Hình 2.10a Hình 2.10b Hình 2.10c

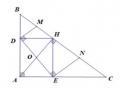
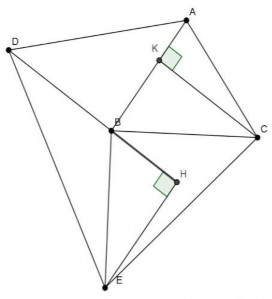
Ví dụ 2.5: Cho tam giác ABC về phía ngoài tam giác dựng các tam giác ABD và BCE

vuông cân tại B. Hãy so sánh diện tích tam giác ABC và BDE.

Hình 2.11

Có thể bạn quan tâm!

Đây là dạng bài toán kết thúc mở HS chưa biết được kết luận cần chứng minh. HS phải đưa ra giả thuyết ngoại suy và sử dụng suy luận ngoại suy để chứng minh được giả thuyết.

C1: Diện tích tam giác ABC bằng diện tích tam giác BDE

D1: ? C1: ? D2: ? C2: EH = CK

W1: Công thức tính diện tích W2: ? D1: BD =AB; đường cao EK và CK

D3: ? C3: BCK = BEH

W3: Định lí các trường hợp bằng nhau của tam giác

D3: BC = BE, BHF = BKC = 900,

?EBH = KBC

D4: C4: EBH = KBC

W4: Quy tắc suy luận

D4: KBC + DBE = 1800;

EBH + DBE = 1800.

HS nhận thấy đáy của hai tam giác ABC và BDE bằng nhau nên HS suy nghĩ đến dựng đường cao từ E và C xuống các đáy BD và AB. Để chứng minh diện tích hai tam giác bằng nhau HS lập luận chứng minh hai đường cao bằng nhau. Để chứng minh hai đường cao bằng nhau cần chứng minh hai tam giác chứa hai đường cao bằng nhau. Và để chứng minh hai tam giác bằng nhau cần chứng minh hai góc EBH = KBC. Khi trình bày lời giải bài toán HS sử dụng suy ngược lùi để chuyển sang chứng minh suy diễn.

Để giải quyết bài toán HS phải sử dụng suy luận ngoại suy để đưa ra kết luận cần chứng minh “Diện tích hai tam giác ABC và BDE bằng nhau”. Trong quá trình tìm con đường giải quyết HS chọn những cách giải đơn giản phù hợp để giải. Sau khi giải quyết xong bài toán HS có thể đặt ra các vấn đề: “Còn cách nào khác không”, “Nếu dựng ra ngoài các tứ trên ba cạnh của tam giác thì các tam giác tạo thành có mối quan hệ gì?”,…

Ví dụ 2.6: Nêu phương án để đo chiều cao của cây thông cao mà không cần thang hay leo lên.

Hình 2.12

Với dạng bài toán kết thúc mở gắn với thực tế HS có thể đưa ra các phương án khác nhau để đo chiều cao của cây và khi đưa ra các phương án HS phải sử dụng lập luận ngoại suy để chọn phương án của mình và tìm các dữ liệu để đưa ra các bước thực hiện các phương án đó. Chẳng hạn HS có thể sử dụng tam giác đồng dạng để đo chiều cao của cột. HS phải suy luận cần làm những bước nào mới tính được chiều cao của cây.

Hình 2.13

Các bước như sau:

- Đặt cọc AC thẳng đứng (vuông góc với mặt đất).

- Điều khiển thước ngắm sao cho đi qua đỉnh C’ của cây. Sau đó xác định giao điểm B của AA’ với CC.

- Đo AA’, AB và chiều cao cọc AC. Sử dụng tam giác đồng dạng để tính chiều cao của cây.

2.2.3. Biện pháp 3: Phát triển khả năng tư duy, dự đoán phát hiện, định hướng lời giải các bài toán hình học lớp 9

a) Cơ sở của biện pháp

Hình học là một bộ môn có nhiều khái niệm trừu tượng nhất, kiến thức trong bài tập lại phong phú, đa dạng hơn rất nhiều so với nội dung lý thuyết mới học. Bên cạnh đó, yêu cầu bài tập lại cao, nhiều bài toán ở dạng chứng minh đòi hỏi phải suy luận chặt chẽ logic và có trình tự. Các kiến thức được trình bày theo con đường kết hợp trực quan và suy luận, lập luận. Bẳng việc quan sát BDTQ, HS dự đoán các kết luận hình học và tiếp cận các định lý. Nhờ đó giúp HS có hứng thú học tập, chịu khó tìm tòi khám phá kiến thức.

Hệ thống các bài tập đa dạng phong phú được thể hiện dưới nhiều hình thức, phần lớn là các bài tập chứng minh, tính toán, từ đó đòi hỏi HS phải có khả năng tư duy, dự đoán, phát hiện, định hướng để tìm được lời giải cho bài toán. Vì vậy, việc hướng dẫn học sinh cách tư duy dự đoán, phát hiện, định hướng tìm lời giải cho bài toán là hết sức quan trọng để khơi dậy hứng thú học tập, giúp học sinh học hình học nhẹ nhàng hào hứng, đạt kết quả tốt hơn.

Biện pháp này giúp HS phát triển khả năng phát hiện quy luật hay tính chất toán học nhờ việc sử dụng năng lực suy luận, khả năng suy luận trả lời được câu hỏi khi giải quyết vấn đề và chứng minh được mệnh đề toán học không quá phức tạp.

b) Cách thức thực hiện

Trong biện pháp này chúng tôi giả định học sinh nắm được các kĩ năng vẽ hình. Trong dạy học, giáo viên có thể hướng dẫn học sinh cách dự đoán, phát hiện, đinh hướng như sau:

Giáo viên đưa ra cho học sinh một ví dụ sau đó yêu cầu học sinh dự đoán kết quả, phát hiện vấn đề của bài toán và định hướng cách giải bài toán thông qua các bước sau:

Bước 1: Cho học sinh quan sát hình vẽ trên phần mềm mà giáo viên đưa ra muốn học sinh dự đoán, pháp hiện và định hướng lời giải.

Bước 2: Dựa trên cơ sở các kiến thức đã học, đưa ra các khả năng có thể xảy ra của bài toán và định hướng cách giải của bài toán (tùy thuộc vào năng lực tư duy của học sinh).

Bước 3: Sau khi làm một vài ví dụ có tính chất như nhau học sinh có thể định hướng cách giải chung cho bài toán.

Giáo viên đưa ra bài toán:

Ví dụ 2.7: Trên trang hình GeoGebra, dựng nửa đường tròn đường kính

AB = a + b; C là một điểm di động trên AB sao cho AC = a; BC = b. Qua C dựng đường thẳng vuông góc với AB cắt nửa đường tròn tại M. Cho HS thay đổi vị trí của C trên đoạn AB và quan sát hình cho biết

a) Xác định theo a, b độ dài cạnh MC của tam giác vuông OMC.

b) So sánh độ dài của các cạnh MC và OM khi a, b thay đổi? Giải thích? Từ đó em hãy suy ra một biểu thức đại số thể hiện mối quan hệ giữa các giá trị không âm a, b.

c) Tìm điều kiện của a, b để MC OM ? Giải thích?

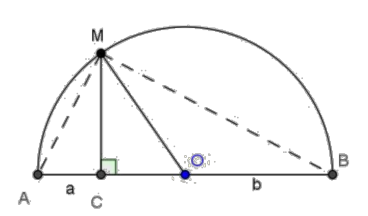
Hình 2.14

HS dễ dàng nhận ra được AMB  900 . Do đó: MAC BMC

Để tìm được a, b để MC = OM, HS cần đi tìm kiếm dữ liệu để đưa ra kết luận. HS suy nghĩ đến tính MC và OM theo a, b. HS tính được MC  theo hệ thức

1 a  b

lượng trong tam giác vuông,

MC  MO 

AB  do tam giác MOC vuông tại

2 2

C. Như vậy ta có

a  b. Để MC = MO HS sử dụng phần mềm Geogebra kéo rê

C  O và nhận thấy a = b.

Gọi H là chân đường vuông góc hạ từ C xuống OM. GV yêu cầu HS như sau:

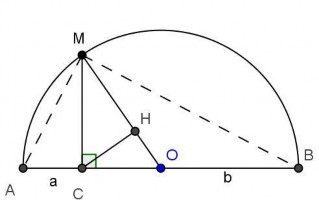
Hình 2.15

d) Xác định theo a, b độ dài cạnh MH của tam giác vuông MHC.

e) So sánh độ dài của các cạnh MC và MH khi a, b thay đổi? Giải thích? Từ đó em hãy suy ra một biểu thức đại số thể hiện mối quan hệ giữa các giá trị không âm a, b.

f) Tìm điều kiện của a, b để MC MH ? Giải thích?

Tương tự như trên HS phải đi tính MH và MC. HS sử dụng hệ thức lượng trong

tam giác vuông MCO suy ra

MH 

2ab a  b

. Từ tính chất trong tam giác vuông MHC

luôn có MH  MC , HS suy ra biểu thức 2ab 

a  b

. Dấu bằng xảy ra khi

C  H  O , tức a = b.

Qua ví dụ trên ta có mối quan hệ2aba  b, dấu bằng xảy khi a = b.

a  b 2

Ví dụ 2.8: Để hình thành khái niệm đường tròn nội tiếp tam giác GV cho HS làm bài tập “Cho tam giác ABC. Gọi I là giao điểm của các đường phân giác các góc trong của tam giác; D, E, F theo thứ tự là chân đường vuông góc kẻ từ I đến các cạnh BC, AC, AB. Nhận xét về mối quan hệ giữa 3 điểm D, E, F”.

GV sử dụng phần mềm hình học Geometer’s Sketchpad vẽ hình. (Hình 2.15). GV thực hiện thao tác di chuyển giúp HS quan sát, dự đoán về mối quan hệ giữa 3 điểm D, E, F.

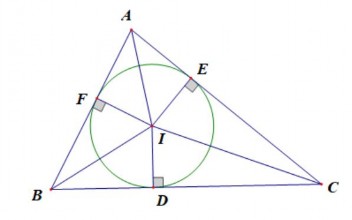
Hình 2.16

HS sẽ thấy: “ Độ dài DI, EI và FI bằng nhau nên 3 điểm D, E, F luôn nằm trên đường tròn tâm I”.

Thật vậy, theo tính chất của tia phân giác, ta có: AI là tia phân giác của góc BAC nên IE = IF. BI là tia phân giác của góc CBA nên IF = ID

Do đó, IE = IF = ID. Vậy 3 điểm D, E, F cùng nằm trên đường tròn tâm I.

Từ đó, HS hình thành khái niệm đường tròn nội tiếp tam giác.

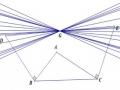
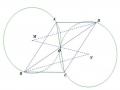
Ví dụ 2.9: Cho nửa đường tròn tâm O đường kính AB = 2R. Một điểm M di chuyển trên nửa đường tròn. Nối AM. Trên tia AM lấy điểm N sao cho AN = BM. Tìm tập hợp các điểm N.

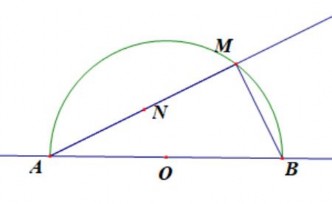
Hình 2.17

GV sử dụng phần mềm hình học Geometer’s Sketchpad vẽ hình. (Hình 2.15). HS thực hiện thao tác di chuyển và quan sát, dự đoán quỹ tích.

Khi M trùng điểm B thì N trùng điểm A. Suy ra A thuộc quỹ tích.

Khi M trùng điểm I (I là điểm nằm chính giữa cung AB) thì N trùng điểm I. Suy

ra I là một điểm thuộc quỹ tích.

Khi M trùng điểm A, N trùng điểm B’ (B’ thuộc tiếp tuyến At sao cho AB’=AB=2R). Suy ra B’ thuộc quỹ tích.

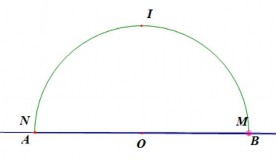
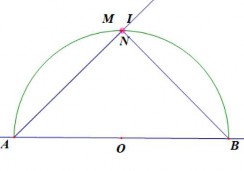
Hình 2.18a Hình 2.18b

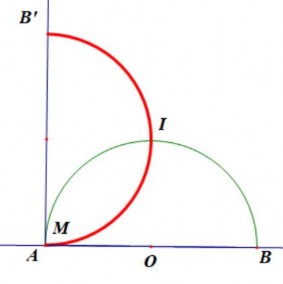
Hình 2.18c

Vậy quỹ tích của N đi qua 3 điểm A, I, B’ không thẳng hàng. HS dự đoán quỹ tích là nửa đường tròn đường kính AB’. Với AB’=AB=2R.

GV sử dụng phần mềm giúp HS kiểm chứng dự đoán.

Xem tất cả 143 trang.

Ngày đăng: 14/06/2022