Biện Pháp 4: Cung Cấp Cho Hs Các Tri Thức Về Các Quy Tắc Suy Luận Lôgic Trong Hình

2.2.4 . Biện pháp 4: Cung cấp cho HS các tri thức về các quy tắc suy luận lôgic trong hình học 9

a) Cơ sở của biện pháp

Theo quan điểm truyền thống thì: Logic học là khoa học nghiên cứu về những quy luật và hình thức (khái niệm, phán đoán, suy luận...) của tư duy chính xác.

Những quy tắc lôgic thường không được trình bày một cách tường minh trong nội dung môn Toán ở trường phổ thông, HS lĩnh hội chúng một cách ẩn tàng thông qua những

trường hợp cụ thể. Thường dùng nhiều nhất là quy tắc có sơ đồ A  B, A . Cùng với

việc nhấn mạnh và làm nổi bật quy tắc lôgic thường dùng trên, GV cần quan tâm dùng

những ví dụ cụ thể bác bỏ những sai lầm do HS thường hay ngộ nhận như A  B, B ,

A  B, A B

Có thể bạn quan tâm!

Xem toàn bộ 143 trang tài liệu này.

động đó.

. Mặt khác cần rèn luyện cho HS những quy tắc ăn khớp với những hoạt

Biện pháp này giúp HS phát triển khả năng phát hiện quy luật hay tính chất toán học nhờ việc sử dụng năng lực suy luận, khả năng kiểm tra, đánh giá các giả thuyết dựa vào các suy luận, khả năng suy luận trả lời được câu hỏi khi giải quyết vấn đề và chứng minh được mệnh đề toán học không quá phức tạp.

b) Cách thức thực hiện

GV có thể cho HS thực hiện theo các bước sau:

- Bước 1: Xây dựng cách chứng minh

- Bước 2: Trình bày lời giải

- Bước 3: Nghiên cứu sâu lời giải

Ví dụ 2.10: Cho hình bình hành ABCD, hai đường chéo cắt nhau tại O. Chứng minh rằng các đường tròn ngoại tiếp AOB và COD tiếp xúc ngoài với nhau.

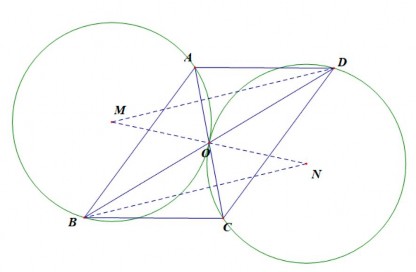
Hình 2.19

Bước 1: Xây dựng cách chứng minh

Để tìm ra kết luận bài toán HS có thể sử dụng các lập luận có cấu trúc như sau:

Để chứng minh các đường tròn ngoại tiếp AOB và COD tiếp xúc ngoài với nhau.

HS xác định luận cứ cần tìm là ba điểm M, O, N thẳng hàng và MN= MO+ON, tức là đoạn nối tâm bằng tổng hai bán kính và luận chứng W: tính chất hai đường nối tâm.

Để chứng minh MO ON MN :

D: ? C: MOON MN

W: ?

HS có thể suy nghĩ đến các cách để chứng minh MO ON MN như tìm độ dài MO, ON nhưng trong trường hợp này không khả quan vì bài toán không cho các yếu tố về độ dài. HS có thể gặp khó khăn ở bước này. GV gợi ý cho HS tính chất: “Hai tam giác bằng nhau thì bán kính hai đường tròn ngoại tiếp hai tam giác bằng nhau”. (Đây

là quy tắc lôgic thông dụng A  B, A )

HS tìm được dữ liệu để chứng minh MO ON MN là chứng minh MO ON và

M, O, N thẳng hàng.

D: ? C: MOON

W: Tính chất đường tròn ngoại tiếp hai tam giác bằng nhau

HS xác định được luận cứ cần tìm D: AOB = COD (đã cho theo giả thiết).

Để giải quyết M, O, N thẳng hàng

D: ? C: M, O, N thẳng hàng.

W: ?

HS cần đi tìm các luận cứ, luận chứng để chứng minh kết luận trên. HS có thể có các hướng chứng minh 3 điểm thẳng hàng:

Hướng 1: Sử dụng tiên đề Ơclit: OM, ON cùng song song với một đường thẳng

cho trước.

Hướng 2: Sử dụng tính chất hình bình hành chứng minh BMDN là hình bình hành

suy ra M, O, N thẳng hàng.

Hướng 3: Sử dụng góc bù: Chứng minh 𝑀̂𝑂𝐷 + 𝑁̂𝑂𝐷 = 180°.

HS lựa chọn con đường nào phù hợp để chứng minh kết luận. HS sử dụng tính chất của hình bình hành:

D: ? C: M, O, N thẳng hàng.

W: tính chất hình bình hành

HS cần chỉ ra luận cứ D: MDNB là hình bình hành. Để chứng minh MDNB là hình bình hành. HS sử dụng dấu hiệu nhận biết hình bình hành.

D: ? C: MDNB là hình bình hành W: Dấu hiệu nhận biết hình bình hành

HS cần chỉ ra MB ND và MB ND . Để chỉ ra HS cần chỉ ra MBO NDO.

Bước 2: Trình bày lời giải

Dựa vào các suy luận có cấu trúc ngoại suy như trên GV cần hướng dẫn HS trình bày lại lời giải bài toán như sau:

Gọi M, N lần lượt là tâm đường tròn ngoại tiếp AOB và COD .

Ta có AOD COB . Do đó các đường tròn ngoại tiếp hai tam giác này bằng

nhau.

MBNDMONO (1).

Xét MDO và NBO có:

MO ON (theo 1)

OB OD (tính chất hình bình hành)

BN DN (theo 1)

MOD NOB (c-c-c).

MBD BDN (tính chất hai tam giác bằng nhau).

ND .

Mà hai góc này ở vị trí so le trong nên MB

Xét tứ giác MBND có MB ND và MB=ND nên MBND là hình bình hành.

Từ đó 3 điểm M, O, N thẳng hàng (2).

Từ (1) và (2) ta có MN=MO+ON tức là đường nối tâm bằng tổng hai bán kính nên hai đường tròn (N) và (M) tiếp xúc ngoài với nhau.

Như vậy để chứng minh bài toán trên ta đã sử dụng quy tắc lôgic rất thông dụng

A  B, A

. GV cǜng cần quan tâm đến những ví dụ cụ thể bác bỏ những sai lầm mà

HS hay mắc phải.

Bước 3: Nghiên cứu sâu lời giải

GV lật ngược vấn đề “Hai tam giác bằng nhau thì hai đường tròn ngoại tiếp hai tam giác đó bằng nhau” liệu “Hai đường tròn ngoại tiếp hai tam giác bằng nhau thì hai tam giác đó bằng nhau”. Nhiều HS cho rằng điều này đúng là đã mắc sai lầm

A  B, B

HS phải kiểm tra lại giả thuyết này và đây là giả thuyết không đúng.

Ví dụ 2.11: Chứng minh định lí “Trong một tam giác vuông, nghịch đảo bình phương đường cao tương ứng với cạnh huyền bằng tổng các nghịch đảo bình phương hai cạnh góc vuông”.

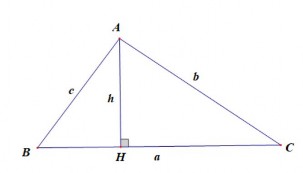
Xét lời giải HS như sau:

Hình 2.20

2 2

1 1 1 1 b  c

h2 b2 c2 h2 b2c2

 (b2  c2 )h2  b2c2

 a2h2  b2c2

 ah = bc 2

Do (2) đúng nên (1) đúng. Vậy định lí được chứng minh.

Sai lầm trong chứng minh này là sai lầm về mặt luận chứng, suy luận không hợp

lôgic vi phạm quy tắc A  B, A , ở đây HS sử dụng quy tắc sai A  B, B .

B A

Biện pháp này giúp HS phát triển khả năng xác định căn cứ ở mỗi bước lập luận của HS, khả năng kiểm tra đánh giá các giả thuyết dựa vào các suy luận.

2.3. Kết luận chương 2

Trong thực tế năng lực suy luận của học sinh lớp 9 còn hạn chế và có nhiều nguyên nhân, nguyên nhân từ GV: không chú ý rèn luyện năng lực suy luận, tạo những tình huống phát triển năng lực suy luận,…. Nguyên nhân từ HS: Suy luận logic, khả năng phán đoán, phát hiện vấn đề của bài toán còn hạn chế, không biết dự đoán, định hướng cho bài toán,…..

Khắc phục tình trạng này, chúng tôi đã trình bày việc xây dựng gồm bốn biện

pháp phát triển năng lực suy luận trong dạy học hình học lớp 9 ở trường THCS đó là:

- Biện pháp 1: sử dụng biểu diễn trực quan động hỗ trợ suy luận;

- Biện pháp 2: Xây dựng bài toán hình học kết thúc mở hỗ trợ HS phát triển khả năng khám phá toán bằng suy luận thông qua việc sử dụng BDTQ.

- Biện pháp 3: Phát triển khả năng tư duy, dự đoán phát hiện, định hướng lời giải các bài toán Hình học lớp 9

- Biện pháp 4: Cung cấp cho HS các tri thức về các quy tắc suy luận lôgic trong hình học 9

Trong từng biện pháp tác giả đã làm rò cơ sở và ý nghĩa của năng lực suy luận

toán học trong dạy học hình hoc 9 ở trường THCS. Các biện pháp trên áp dụng được

trong cả các tiết lí thuyết và bài tập, giúp HS chủ động nắm vững và tiếp thu kiến thức một cách sáng tạo. Qua đó, phân tích làm rò các vấn đề mà HS thường gặp khó khăn khi giải quyết vấn đề của bài toán Hình học lớp 9 cho học sinh THCS.

Nội dung chương này được thiết kế nhằm định hướng cho quá trình thực nghiệm sư phạm ở chương 3.

Chương 3

THỰC NGHIỆM SƯ PHẠM

3.1. Mục đích thực nghiệm sư phạm

Thực nghiệm các biện pháp sư phạm để kiểm chứng tính khả thi và hiệu quả của các biện pháp sư phạm nhằm phát triển năng lực suy luận ngoại suy cho HS THCS trong dạy học Hình học 9 đã được trình bày trong luận văn.

3.2. Nội dung, kế hoạch và phương pháp thực nghiệm

3.2.1. Nội dung thực nghiệm sư phạm

Dạy học hình học lớp 9 cho học sinh theo hướng phát triển năng lực suy luận toán học bằng hình thức tổ chức hoat động nhóm, hoạt động lớp thông qua kế hoạch dạy học thông qua 3 tiết dạy sau:

* Tiết 1: “Góc có đỉnh ở bên trong đường tròn. Góc có đỉnh ở bên ngoài đường tròn”

* Tiết 2: “Cung chứa góc. Luyện tập”

* Tiết 3: “Tứ giác nội tiếp”

Các thực nghiệm được thiết kế và hướng dẫn HS ghi chép, giải toán sử dụng suy luận hình học 9. Thực nghiệm sư phạm được tiến hành đối với HS lớp 9 của trường THCS Chu Văn An – Thành phố Thái Nguyên – tỉnh Thái Nguyên.

Được sự đồng ý của Ban giám hiệu và cô giáo: Cô giáo – Lê Thị Lan dạy lớp đối chứng, lớp thực nghiệm do trực tiếp tác giả luận văn giảng dạy, tác giả luận văn đã tiến hành thực nghiệm sư phạm. Ở các lớp thực nghiệm, GV dạy theo bài soạn thực nghiệm đã soạn.

Đối với các lớp đối chứng, GV sử dụng phương pháp dạy học thông thường. Đối với các lớp thực nghiệm, GV chú ý sử dụng BDTQ (phần mềm hình học động) phát triển năng lực suy luận cho HS.

Trong các giờ dạy học thực nghiệm, tác giả luận văn xây dựng mục tiêu giờ học cho cả lớp học, các nội dung giờ học cǜng được lựa chọn cho phù hợp, để đáp ứng mục tiêu đã đề ra. Để có mục tiêu phù hợp chung cho đa số HS, tác giả luận văn dựa trên các cơ sở:

+ Mục tiêu giáo dục.

+ Khối lượng và mức độ kiến thức, kỹ năng HS đã có trên cơ sở khảo sát bằng các phiếu hỏi, qua quan sát, qua xem xét môi trường sống của HS.

+ Căn cứ vào chuẩn kiến thức được quy định trong tài liệu chỉ đạo chuyên môn.

+ Yêu cầu bài học theo sách dành cho GV.

3.2.2. Kế hoạch thực nghiệm sư phạm

Quá trình thực nghiệm sư phạm được tiến hành tại trường THCS Chu Văn An – Thành phố Thái Nguyên, tỉnh Thái Nguyên. Việc thực nghiệm sư phạm được tiến hành trên 2 lớp 9A1 và 9A3.

Sĩ số các lớp và GV dạy như sau:

- Lớp 9A1 sĩ số 45 HS: là lớp thực nghiệm do tác giả luận văn trực tiếp giảng

dạy.

- Lớp 9A3 sĩ số 45 HS: là lớp đối chứng, do cô giáo Lê Thị Lan trực tiếp giảng

3.2.3. Phương pháp thực nghiệm sư phạm

Hiệu quả của việc sử dụng BDTQ phát triển suy luận thông qua dạy học hình học 9 được tác giả luận văn đánh giá trên cơ sở.

+ Sự hiểu biết của HS về kiến thức của tiết học.

+ Kiểm tra kiến thức từng cá nhân HS của lớp thực nghiệm và lớp đối chứng thông qua bài kiểm tra tự luận sau nội dung thực nghiệm.

+ Sử dụng phiếu khảo sát dành cho HS với các câu hỏi kiểm tra sự hiểu biết của HS về nội dung kiến thức, khả năng thể hiện mình của từng HS.

+ Sự tiến bộ của HS trong học tập nói chung: Thông qua quan sát và đánh giá của các GV khác, qua phụ huynh HS thông qua học tập, rèn luyện ở trường cǜng như ở nhà.

Để đánh giá những nội dung trên, chúng tôi sử dụng các công cụ:

Kiểm tra tự luận: Nhằm đánh giá mức độ lĩnh hội bài học của HS qua các tiết học. Kiểm tra kiến thức của từng cá nhân của lớp thực nghiệm và lớp đối chứng thông qua bài kiểm tra tự luận. Nội dung kiểm tra dựa vào các câu hỏi trong SGK và mục tiêu giờ học trong kế hoạch bài học. Tất cả các bài kiểm tra được một người chấm theo điểm số trung bình cộng của cả đợt. Kiểm tra nhằm: