Vai Trò Của Giáo Viên Trong Quá Trình Suy Luận Của Học Sinh

Hình vẽ:

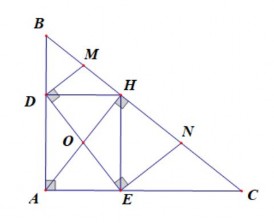
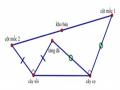
Hình 1.14

C1: DE

D1: ? C1:?

W: ?

D2: ? C2: ADEH là hình chữ nhật

W: Dấu hiệu nhận biết hình chữ nhật

D2: ADH HDA AEH  90o D3: ? C3: AH DE

W: Tính chất hình chữ nhật

D3: ADEH là hình chữ nhật

Trong quá trình đi tính DE HS không tìm được trực tiếp DE HS phải đi tìm kiếm dữ liệu để tính DE đó là AH.

D4: ? C4: AH

W: Hệ thức lượng trong tam giác

D4: BH  4cm ; CH  9cm

D5: ? C5: MH MB

W: ?

Đây là ngoại suy sáng tạo, HS phải tìm các dữ liệu để chứng minh MH MB .

HS đưa ra giả thuyết DBM DMH . HS sử dụng quy tắc bắc cầu DBM HCA

vì cùng bằng BHD và quy tắc suy luận A B , B.

(DBM HCA ABC cân nhưng ABC không cân nên hai góc trên không bằng nhau dẫn đến điều giả sử là sai).

Để chứng minh M là trung điểm của BH HS đã sử dụng quy tắc bắc cầu để xác con đường chứng minh.

D6: ? C6: DM MH

W: tính chất bắc cầu

D6: DM MH; BM DM

D7: ? C7: DM MH

W: tính chất hai tam giác bằng nhau

D7: DOM HOM

D8: ? C8: DM MH

W: Định lí hai tam giác bằng nhau

D8: OM chung; DO HO ?

Như vậy để chỉ ra DM MH, HS tìm kiếm các dữ liệu để chứng minh hai tam giác

DOM HOM, HS đã sử dụng các suy luận ngoại suy đơn tuyến cần tìm các luận chứng để tìm ra con đường chứng minh.

D9: ? C9: BM DM

W: ?

Đây là ngoại suy sáng tạo HS cần tìm cả luận cứ và luận chứng để chứng minh

BM DM . HS đưa ra các giả thuyết liệu hai đoạn thẳng trên có cùng bằng đoạn nào không và bác bỏ giả thuyết này, sau đó HS suy nghĩ đến chứng minh BDM cân. Để khẳng định con đường chứng minh của mình HS đã sử dụng quy tắc bắc cầu chứng minh hai góc bằng nhau.

D10: ? C10: BMD cân tại M

W: Định lí tam giác cân

Tóm lại, khi đưa ra một giả thuyết HS cần nắm vững các quy tắc suy luận để vận dụng các quy tắc suy luận kiểm tra tính đúng đắn của giả thuyết mới định hướng được con đường giải quyết các vấn đề đặt ra. Nếu HS không nắm được các suy luận rất có thể bị sai lầm trong chứng minh hoặc không tìm ra đường con đường chứng minh.

e) Thành tố 5: Khả năng suy luận trả lời được câu hỏi khi giải quyết vấn đề và

chứng minh được mệnh đề toán học không quá phức tạp.

Quá trình giải toán, trả lời các câu hỏi khi chứng minh hình học hay giải quyết vấn đề ở bậc THCS đòi hỏi sự sáng tạo, sâu sắc hơn về mặt kiến thức và sử dụng ngôn ngữ, kí hiệu cǜng như các định nghĩa, định lý, tính chất … đã có. Vì thế, trong các hoạt động cần được “nhúng” vào trong môi trường khám phá, phát minh lại tri thức để người học có thể thấy được “quá trình” sáng tạo. Quá trình này nhằm làm giảm bớt các thủ thuật trong giải toán, chứng minh và giúp cho người học làm quen với con đường tiếp cận giải quyết vấn đề, chứng minh các mệnh đề không quá phức tạp của toán học.

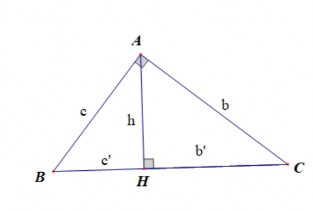
Ví dụ 1.12 Trong một tam giác vuông, bình phương đường cao ứng với cạnh huyền bằng tích hai hình chiếu của hai cạnh góc vuông trên cạnh huyền.

Hình 1.15

Chứng minh:

Từ ∆𝐴𝐻𝐵~∆𝐶𝐻𝐴 (g-g) =>𝐴𝐻 = 𝐶𝐻 =>𝐴𝐻2 = 𝐻𝐵. 𝐻𝐶 => h2=b’.c’

𝐵𝐻 𝐴𝐻

1.5.3 Vai trò của giáo viên trong quá trình suy luận của học sinh

HS thường gặp nhiều khó khăn trong quá trình sử dụng các phương pháp suy luận để giải các bài toán hình học. Do đó, giáo viên có vai trò quan trọng trong việc hỗ trợ, hướng dẫn, gợi ý cho học sinh trong quá trình suy luận. Theo Pedemonte (2010, [42]):

- Giáo viên có thể gợi ý, hướng dẫn cho học sinh tìm mối liên hệ giữa các dữ liệu đã có và hỗ trợ cho học sinh trong việc lựa chọn một quy tắc suy luận (định lý) phù hợp để xây dựng một lập luận có cấu trúc suy diễn;

- Giáo viên có thể gợi ý hoặc khẳng định cho học sinh một quy tắc suy luận phù hợp nhất;

- Giáo viên có thể sử dụng các BDTQ nhằm giúp HS tìm ra các phương pháp suy luận thích hợp.

Đặc biệt, phương pháp giảng dạy của giáo viên cǜng có vai trò quan trọng trong quá trình suy luận của học sinh, bởi nó có liên quan đến khả năng đưa ra các giả thuyết ban đầu của học sinh trước khi bắt đầu giải quyết một bài toán (Pedemonte, 2010, [42]). Đồng thời giáo viên cǜng có vai trò trong việc thúc đẩy các hoạt động tranh luận của học sinh. Như các nghiên cứu thực nghiệm của Boero, Garuti và Mariotti (1996, [34]) đã chỉ ra rằng càng thúc đẩy và phát triển các hoạt động tranh luận của học sinh sẽ giúp học sinh dễ tiếp cận với cách giải quyết bài toán hơn. [23]

1.6. Thực trạng của việc sử dụng biểu diễn trực quan phát triển năng lực suy luận trong dạy và học hình học cho học sinh lớp 9 ở trường THCS

1.6.1. Nội dung hình học lớp 9

Chương trình hình học 9 được xây dựng gồm có 4 chương: Chương 1: Hệ thức lượng trong tam giác vuông;

Chương 2: Đường tròn; Chương 3: Góc và đường tròn;

Chương 4: Hình trụ- Hình nón- Hình cầu.

Chương 1: Chương này các kiến thức trong chương được trình bày trong sách giáo khoa GV khá đơn giản, chỉ cần dẫn dắt gợi mở để HS tự tìm ra kiến thức.

Chương 2: HS tìm hiểu về các tính chất trong một đường tròn (sự xác định một đường tròn, tính chất đối xứng, liên hệ giữa đường kính và dây, liên hệ giữa dây và khoảng cách từ tâm đến dây), vị trí tương đối của đường thẳng và đường tròn, vị trí tương đối của đường tròn với đường tròn, đường tròn nội tiếp, đường tròn ngoại tiếp, đường tròn bàng tiếp tam giác. Trong chương này yêu cầu chứng minh định lí được nâng cao hơn so với các lớp dưới. Nhiều định lí được chứng minh đầy đủ, tuy nhiên vì lí do sư phạm có những định lí không ghi phần chứng minh mà chỉ thông qua các câu hỏi, có những định lí được công nhận. Các bài tập về tính toán và chứng minh ở chương này chiếm số lượng lớn. Có những bài tập dựng hình, thường là các bài không phức tạp, các bài tập hợp điểm chỉ hạn chế ở mức độ phát biểu tập hợp. Trong chương này GV có thể sử dụng các công cụ hình thức trực quan chẳng hạn khi di chuyển đường thẳng và đường tròn… khi dạy về vị trí tương đối của đường thẳng và đường tròn.

Chương 3: Sau khi học về góc (lớp 6, 7) và đường tròn chương trước HS thiết lập được các khái niệm về góc liên hệ với đường tròn. Các định lí tiếp tục yêu cầu được chứng minh đầy đủ, các bài tập dạng dựng hình quỹ tích yêu cầu ở mức độ cao hơn. Đây là dạng bài tập khó với HS. GV nên sử dụng các phần mềm toán học BDTQ để hỗ trợ HS suy luận tìm ra vấn đề cần giải quyết.

Chương 4: Đối với chương trình Toán ở trường THCS thì chương này nhằm hoàn chỉnh chủ đề “các vật thể không gian” của chương trình toán học ở bậc này. Trong chương này thông qua một số hoạt động như quan sát mô hình, nhận xét mô hình HS nhớ lại, xây dựng và củng cố công thức đã học, tiếp cận được khái niệm và các yếu tố của hình trụ, hình nón, hình cầu. Thông qua quan sát và thực hành, HS nắm vững các công thức được thừa nhận. Đặc biệt phần bài tập trình bày khá nhiều các bài tập có nguồn gốc đời sống thực tế.

1.6.2 Thực trạng của việc sử dụng biểu diễn trực quan phát triển năng lực suy luận trong dạy và học hình học cho học sinh lớp 9 ở trường THCS

Để tìm hiểu thực trạng việc dạy học nội dung Hình học trường THCS nói chung và dạy học Hình học 9 theo định hướng phát triển năng lực suy luận thông qua sử dụng

biểu diễn trực quan, tác giả luận văn đã tiến hành điều tra, khảo sát, lấy ý kiến của 10 GV và 120 HS của trường THCS Chu Văn An, thành phố Thái Nguyên, tỉnh Thái Nguyên. Kết quả khảo sát như sau:

a) Giáo viên

Để tìm hiểu về thực trạng dạy học nội dung Hình học 9, chúng tôi đã tiến hành phỏng vấn, phát phiếu điều tra xin ý kiến của 10 GV dạy toán thuộc trường THCS Chu Văn An.

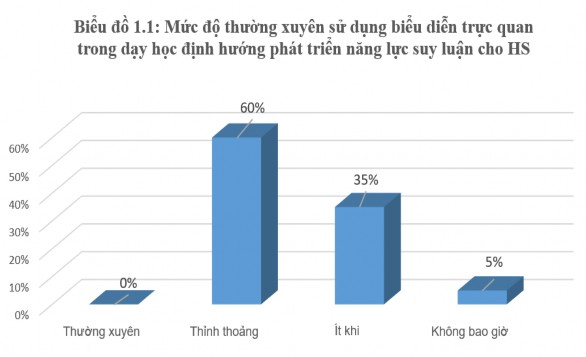
Nội dung tổng hợp từ các phiếu điều tra được thể hiện trong các biểu đồ sau:

1. Thầy, cô biết sử dụng biểu diễn trực quan trong dạy học hình học qua nguồn

nào?

Phương pháp lựa chọn	Tỉ lệ %
a) Từ tập huấn chuyên môn	40
b) Qua internet, tài liệu tham khảo	52
c) Từ đồng nghiệp	58
2. Hiệu quả của các giờ học hình học có sử dụng biểu diễn trực quan?
Nội dung	Mức độ %

Có thể bạn quan tâm!

Xem toàn bộ 143 trang tài liệu này.

Rất tốt	Tốt	Chưa tốt
Mức độ hiểu bài	42	48	10
Mức độ tích cực, chủ động	46	48	6
Mức độ vận dụng suy luận giải bài tập	45	46	9
3. Dự định của thầy cô trong việc sử dụng BDTQ động hỗ trợ HS phát triên năng lực suy luận?
Phương án lựa chọn		Kết quả (%)
Sẽ vận dụng		75
Chưa rò		25
Không vận dụng		0
4. Thầy cô thường sử dụng phần mềm hình học động nào phục vụ cho việc dạy học hình học?
Phương án lựa chọn		Kết quả (%)
Geogebra		40
Geometer’s Sketchpad		55
Geospace		3
Phần mềm khác		2
5. Thầy cô thường sử dụng phần mềm hình học động trong giờ học toán nhằm mục đích gì?
Vẽ hình cho HS quan sát		100
HS được thao tác khám phá toán học		60
Phát triển khả năng tư duy, dự đoán, khám phá toán học		70
Mục đích khác		30

Bảng 1.4 Kết quả điều tra thực trạng sử dụng BDTQ trong dạy học hình học 9 nhằm phát triển năng lực suy luận cho HS.

Tác giả luận văn đã tiến hành phỏng vấn một số GV ở trường THCS Chu Văn An, tôi xin trích dẫn một đoạn phỏng vấn cô Lê Thị Lan, GV trường THCS Chu Văn An, thành phố Thái Nguyên như sau:

1. Hỏi: Theo cô, khi dạy học nội dung Hình học 9 theo định hướng phát triển năng lực suy luận cho HS, GV thường hay mắc phải những khó khăn như thế nào?

Trả lời: Qua thực tế dạy học, tôi thấy nội dung hình học 9 là một trong những nội dung khó học đối với HS. HS thường lúng túng trong việc suy luận tìm cách giải cho các bài toán, không biết cách nhìn hình để từ những căn cứ bài cho tìm ra lời giải.

2. Hỏi: Cô cho biết nguyên nhân gì dẫn đến những khó khăn đó và cách khắc phục

ra sao?

Trả lời: Theo tôi, những nguyên nhân dẫn đến thực trạng trên là:

+ Do HS quen với cách học thụ động, GV hướng dẫn cụ thể cách giải và làm bài tương tự.

+ Do HS chưa tạo cho mình thói quen tự suy nghĩ độc lập, suy luận từ giả thiết bài toán để tìm ra cách giải.

+ HS chưa biết cách quan sát, dự đoán, liên kết các yếu tố hình học để từ đó suy

luận giải bài toán.

Để có thể khắc phục thực trạng trên, theo tôi, GV cần sử dụng các phần mềm hình học, biểu diễn hình học một cách trực quan để HS quan sát, dự đoán từ đó suy luận tìm ra lời giải.

3. Hỏi: Theo cô, việc sử dụng BDTQ trong dạy học phát triển năng lực suy luận có những ảnh hưởng như thế nào tới HS?

Trả lời: Trong môn hình học 9, việc sử dụng BDTQ có những ảnh hưởng rất tích cực tới HS như là tạo được hứng thú của HS đối với môn học, HS chủ động trong việc suy luận tìm ra lời giải các bài toán khó và HS hiểu sâu hơn các kiến thức.

Tổng hợp kết quả từ các phiếu điều tra, tôi rút ra một số nhận xét:

- GV đã định hướng và tổ chức quá trình dạy học bằng phương pháp dạy học tích cực nhưng việc phát huy tính tích cực, chủ động của HS chưa thật sự hiệu quả.

- GV chưa chú ý nhiều đến cách suy luận tìm ra lời giải bài tập của HS cǜng như cho HS tự đưa ra các dạng bài tập sau mỗi bài toán có thể nghiên cứu sâu.