Cấu Trúc Của Suy Luận Diễn Dịch, Ngoại Suy, Quy Nạp Dựa Trên Mô Hình

Mô hình Toulmin có thể được dùng để mô tả suy luận trong tình huống cần tìm luận cứ hoặc luận chứng để chứng minh cho giả thuyết (kết luận) đã có.

1.4.2 Mô hình Toulmin trong suy luận

Trong các tài liệu về giáo dục, mô hình Toulmin đã được các nhà nghiên cứu sử dụng để phân tích về lập luận và suy luận.

Mô hình Toulmin cǜng được sử dụng bởi nhiều nhà nghiên cứu trong giáo dục toán học (Inglis, Mejia-Ramos, và Simpson, 2007, [34]; Lavy, 2006, [34]) để kiểm tra các lập luận toán học của học sinh. Mô hình Toulmin trong các nghiên cứu của Paolo Boero, Nadia Douek, Francesca Morselli, và Bettina Pedemonte (2010, [33])… cǜng có ý nghĩa quan trọng trong việc so sánh các lập luận của học sinh và các suy luận trong các bài toán chứng minh (Pedemonte 2005, [34]; Pedemonte, 2007, [38];

Pedemonte, 2008, [42]; Pedemonte, 2010, [38]; Pedemonte, 2014, [42]). [20]

Có thể nói, mô hình Toulmin là một công cụ phương pháp luận trong các nghiên cứu về lập luận và chứng minh, đặc biệt là để phân tích mối liên hệ cấu trúc giữa lập luận và chứng minh trong những năm gần đây. Trong nghiên cứu này, chúng tôi chỉ sử dụng mô hình Toulmin cơ bản để phân tích cấu trúc của các bước suy luận trong bài toán hình học. [23]

1.4.3 Cấu trúc của suy luận diễn dịch, ngoại suy, quy nạp dựa trên mô hình

Toulmin

Một bước suy luận suy diễn được trình bày trong mô hình Toulmin có cấu trúc như sau: [23]

D : A C : B

W:AB

Hình 1.6: Mô hình Toulmin của một bước suy luận suy diễn

Trong đó:

A⇒ B là một quy tắc (hoặc định lý, nguyên lý…) A: giả thiết hoặc các dữ liệu cần thiết.

B: là kết luận.

Kết luận của phát biểu được suy ra từ các dữ liệu và quy tắc suy luận cho trước. Một bước ngoại suy được trình bày trong mô hình Toulmin có cấu trúc như sau:

D : ? C : B

W:AB

Hình 1.7: Mô hình Toulmin của một bước suy luận ngoại suy

Dấu hỏi ở trên có nghĩa là dữ liệu sẽ được tìm kiếm để có thể áp dụng quy tắc suy luận biện minh cho phát biểu B. Mǜi tên luôn hướng về kết luận vì kết luận là đối tượng mà ta cần phải đi tìm các dữ liệu và quy tắc suy luận phù hợp để biện minh cho nó.

Quá trình suy luận quy nạp khác với diễn dịch và ngoại suy. Nó được xây dựng bằng việc khái quát hoá (KQH) các phát biểu hoặc bằng các lập luận đã được quan sát hay nghiên cứu. Hai quá trình quy nạp (Harel, 2001, [38]) được phân tích trên mô hình Toulmin là:

+ Khái quát hoá kết quả

+ Khái quát hoá quá trình

Khái quát hoá kết quả được trình bày trong mô hình Toulmin có cấu trúc như hình 1.8:

D: E1, E2, ..., En C: Phát biểu

W: Khái quát hóa kết quả

Hình 1.8: Mô hình Toulmin của một suy luận quy nạp bằng KQH kết quả

Khái quát hoá kết quả chú ý đến tính quy tắc ở các kết quả có được trước đó : E1, E2, ..., En Ở đây C là phát biểu khái quát từ các kết quả E1, E2, ..., En.

Khái quát hoá quá trình được trình bày trong mô hình Toulmin có cấu trúc như hình 2.6:

D: E1 , E1 E2 , E2 E3 ,... C: Phát biểu

W: Khái quát hóa quá trình

Hình 1.9: Mô hình Toulmin của một suy luận quy nạp bằng khái quát hoá quá trình

Khái quát hoá quá trình chú ý đến tính quy tắc ở các quá trình suy luận trước đó

E1 , E1 E2 , E2 E3 ,... Ở đây C là phát biểu khái quát các quá trình suy luận E1 , E1

E2 , E2 E3,... [23]

1.5 Năng lực suy luận

1.5.1 Khái niệm

Từ cách hiểu về các khái niệm suy luận, có thể hiểu năng lực suy luận trong hoạt động toán học của HS như sau: “Năng lực suy luận là năng lực dựa trên những tri thức có giá trị chân thực để liên kết chúng lại với nhau nhằm rút ra tri thức mới mà ta chưa biết ở trong các phán đoán trước đó” [10].

Năng lực suy luận là năng lực sử hoạt động của chủ thể sử dụng các phương pháp suy luận như diễn dịch, quy nạp hay ngoại suy để tìm ra các cách thức giải quyết vấn đề.

1.5.2. Các thành tố cơ bản của năng lực suy luận

Thông qua nghiên cứu về năng lực suy luận kết hợp với quá trình thực nghiệm, phân tích suy luận của các nhóm HS, từ đó có thể đề xuất lăm thành tố của năng lực suy luận:

a) Thành tố 1: Khả năng quan sát những biểu diễn trực quan đưa ra những giả thuyết mới và tiến hành tổng quát hóa

Theo Arcavi (2003): Trực quan hóa là quá trình và sản phẩm của sự sáng tạo, giải thích, sử dụng và phản ánh dựa trên các hình vẽ (hay hình ảnh sơ đồ…) trong đầu chúng ta, trên giấy hay trên các công cụ khoa học công nghệ. Trực quan hóa nhằm mô tả giao tiếp thông tin, tư duy và phát triển các ý tưởng chưa biết trước đó để hiểu. Các biểu diễn trực quan như hình vẽ, đồ thị, sơ đồ, bảng biểu được xem là công cụ để trực quan hóa nhằm giúp HS hiểu được các đối tượng trừu tượng. Biểu diễn trực quan được thừa nhận như là một thành phần chính của suy luận. Nó định hướng và hỗ trợ tích cực cho quá trình giải quyết vấn đề. Đặc biệt là biểu diễn trực quan động với sự hỗ trợ của máy tính đã và đang có nhiều đóng góp trong việc khám phá tri thức mới [24].

Trong môi trường học tập với sự hỗ trợ của biểu diễn trực quan động HS có điều kiện để tiến hành các thử nghiệm toán học thông qua thao tác trên các đối tượng được biểu

diễn. Với các kết quả quan sát được cho các trường hợp riêng, HS vận dụng các suy luận quy nạp và suy luận ngoại suy để đưa ra các phỏng đoán, đề xuất các giả thuyết, khám phá các quy luật và mối quan hệ mới, hay xây dựng các lí giải.

Ví dụ 1.8. Cho hai hình vuông ABCD và EFGH cạnh a, được đặt sao cho đỉnh E trùng với tâm của ABCD còn đình F có thể di chuyển được. Khi di chuyển F nhận xét về phần giao của hai hình vuông.

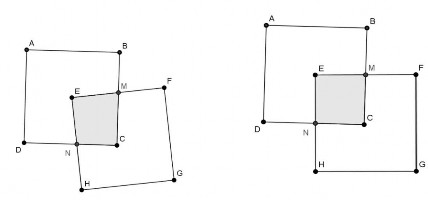
Hình 1.10 Hình1.11

Đầu tiên HS quan sát hình vẽ và sẽ suy nghĩ đến hình dạng của tứ giác EMCN có phải là tứ giác đặc biệt không? Và HS sẽ bác bỏ ngay giả thuyết này khi kéo rê vị trí của điểm F. HS tiếp tục quan sát suy nghĩ và đưa ra giả thuyết về mối quan hệ giữa hai đường chéo của tứ giác trên liệu có vuông góc hoặc bằng nhau không? Và HS cǜng bác bỏ luôn giả thuyết khi kéo rê ngẫu nhiên điểm F và nhận thấy giá trị của góc giữa hai đường chéo và độ dài hai đường chéo không luôn bằng nhau. Trong quá trình kéo rê điểm F HS nhận thấy một trường hợp đặc biệt khi tứ giác EMCN là hình vuông

(Hình1.7) thì diện tích tứ giác EMCN bằng

diện tích tứ giác ABCD không đổi. HS

đưa ra giả thuyết: “Diện tích tứ giác EMNC không đổi và bằng 1 𝑎2”. HS kiểm tra tính

đúng đắn của giả thuyết bằng công cụ đo đạc tính toán và nhận thấy giả thuyết trên là đúng. HS tìm cách chứng minh giả thuyết trên.

Ta có cấu trúc ngoại suy như sau:

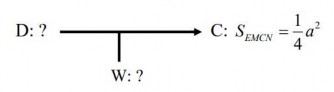
HS phải tìm kiếm dữ liệu để chứng minh cho kết luận S

EMCN

= 𝑎2 . Dựa vào kéo rê

vào trường hợp đặc biệt như trên HS suy nghĩ đến kẻ đường cao từ E xuống BC và DC và đi chứng minh hai tam giác bằng nhau EMH và ENK (với H, K là chân đường cao hạ từ E xuống BC và DC) từ đó có được điều phải chứng minh.

Như vậy, nếu có năng lực quan sát biểu diễn trực quan để đưa ra những giả thuyết mới và tiến hành tổng quát hóa HS sẽ dễ dàng khám phá được các tri thức mới, giải quyết được các dạng bài toán khó, nhất là các bài toán quỹ tích và các bài toán dạng kết thúc mở.

b) Thành tố 2: Khả năng phát hiện quy luật hay tính chất toán học nhờ việc sử dụng năng lực suy luận

Khi phải khám phá một quy luật hay tính chất toán học để đưa ngay ra kết quả là một việc khó khăn. HS sử dụng suy luận ngoại suy để bước đầu khám phá giả thuyết mang tính thăm dò nhằm giải thích cho một số trường hợp đã biết. Sau đó HS mở rộng giả thuyết này bằng cách kiểm chứng cho các trường hợp chưa biết bằng suy luận quy nạp nhằm tăng cường tính có lí của các giả thuyết hay tiến hành một phép suy luận ngoại suy khác khi có một phản ví dụ hay khi tổng quát hóa nên là quá khó. Suy luận ngoại suy sẽ hỗ trợ suy luận quy nạp tìm ra một giả thuyết mang tính tổng quát hóa nhằm giải quyết nhiệm vụ đặt ra. [14]

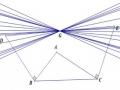
Ví dụ 1.9 GV yêu cầu HS thực hiện theo nhóm cho biết “Có bao nhiêu cặp đối đỉnh được tạo ra bởi n đường thẳng phân biệt”.

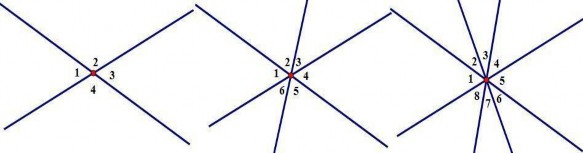
Hình 1.12. Cặp góc đối đỉnh tạo bởi các đường thẳng đồng quy

Một số HS có thể đưa ra ngay câu trả lời, nhưng một số khác có thể sẽ cảm thấy giải bài toán trực tiếp là một nhiệm vụ khó khăn. HS có thể nghĩ đến giải các bài toán đơn giản hơn.

Với 1 đường thẳng, có 0 cặp góc đối đỉnh. Với 2 đường thẳng, có 2 cặp góc đối đỉnh: (1-3) và (2-4). Với 3 đường thẳng, có 6 cặp góc đối đỉnh: (1-4); (2-5); (3-6);(1,2-

4,5); (2,3-5,6) và (3,4-1,6). Tương tự với 4, 5, 6 đường thẳng có tương ứng 12, 20, 30

cặp góc đối đỉnh (Hình 1.9). Tổ chức dữ liệu vào bảng như sau:

Bảng 1.3. Bảng dữ liệu về số đường thẳng và số cặp góc đối đỉnh tương ứng

Số đường thẳng

1	2	3	4	5	6
Số cặp góc đối đỉnh	0	2	6	12	20	30

Có thể bạn quan tâm!

Xem toàn bộ 143 trang tài liệu này.

HS cố gắng đề xuất một giả thuyết về mối quan hệ giữa các dữ liệu thu thập được bằng suy luận ngoại suy, chẳng hạn như mối quan hệ giữa số cặp góc đối đỉnh mỗi khi số đường thẳng tăng thêm một:

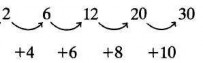
Nhưng HS gặp khó khăn trong việc tổng quát hóa bằng quy nạp nên HS đã đưa ra giả thuyết ngoại suy khác về quan hệ giữa đường thẳng và số cặp góc đối đỉnh được tạo ra: T n. n 1trong đó T là số cặp góc được tạo thành bởi n đường thẳng. Sau đó HS phải sử dụng suy luận quy nạp để kiểm tra giả thuyết mình đưa ra.

Như vậy, suy luận ngoại suy khi kết hợp với quy nạp giúp HS đưa ra những giả thuyết mang tính tổng quát hóa, làm tiền đề cho việc khám phá các quy luật toán và mở rộng hơn là khám phá các tính chất, các định lí toán học cơ bản. [14]

c) Thành tố 3: Thực hiện được việc suy luận hợp lí khi giải quyết vấn đề.

Đây là khả năng mà HS sử dụng căn cứ của mỗi bước lập luận trong trình bày lời giải bài toán. Các căn cứ chính là định nghĩa, định lý hay tiên đề được thừa nhận đưa vào trong các bước lập luận chứng minh của các em.

Ví dụ dưới đây cho ta thấy các căn cứ mỗi bước lập luận trong chứng minh bài toán của HS theo mô hình suy luận Toulmin. Trong phân tích lập luận chúng tôi kí

hiệu Di, Ci và Wi lần lượt là các luận cứ, kết luận và luận chứng.

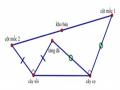
Ví dụ 1.10 Cho tam giác ABC, dựng về phía ngoài tam giác các tam giác ABD và BCE

vuông cân tại B. Hãy so sánh diện tích tam giác ABC và BDE.

HS nhận thấy hai tam giác cần so sánh có hai cạnh bằng nhau (BD = BA) nên

dựng hai đường cao EH và CK tương ứng.

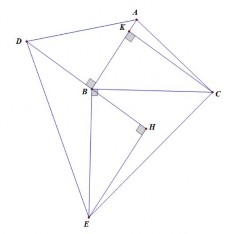
Hình 1.13

HS lập luận vì đáy bằng nhau nên cần so sánh hai đường cao EH và CK.

C1: Diện tích tam giác ABC bằng diện tích tam giác BDE

D1: ? C1: ?

W1: Công thức tính diện tích

D1: BD AB ; đường cao EH và CK

D2: C2: EH = CK

W2: ?

HS lập luận hai đường cao EH và CK bằng nhau bằng việc tìm kiếm các dữ liệu để xác minh hai tam giác BCK và tam giác BEH bằng nhau.

D3: ? C3: BCK = BEH

W3: Định lí các trường hợp bằng nhau của tam giác

D3: BC = BE, BHF = BKC = 900, ?EBH = KBC

D4: C4: EBH = KBC

W4: Quy tắc suy luận

D4: KBC + DBE = 1800; EBH + DBE = 1800.

Như vậy, HS đã chứng minh hai tam giác bằng nhau để giải quyết bài toán. Từ đó, HS bắt đầu bằng việc chứng minh hai cạnh của hai tam giác bằng nhau.

Ta thấy trong từng bước suy luận HS cần phải xác định được các căn cứ, căn cứ đúng mới có thể đưa ra hướng làm đúng, nếu các căn cứ sai thì dẫn đến chứng minh sai. Vì vậy GV cần rèn luyện cho HS luôn luôn xác định căn cứ trong các bước lập luận của mình.

d, Thành tố 4: Khả năng kiểm tra, đánh giá các giả thuyết dựa vào các suy luận

Trong quá trình HS lập luận để tìm ra cách giải quyết các vấn đề đặt ra HS sẽ đưa ra các giả thuyết dựa trên quan sát của mình, các giả thuyết có thể đúng có thể sai. HS cần phải hiểu và áp dụng các quy tắc như các tam đoạn luận phổ biến, quy tắc kết luận từ mệnh đề phổ biến… để kiểm tra tính đúng đắn của giả thuyết mình đặt ra. Nếu giả thuyết đúng HS sẽ tiếp tục con đường đó còn nếu sai HS phải bác bỏ giả thuyết để tìm ra con đường chứng minh khác.

Ví dụ dưới đây cho ta thấy các căn cứ mỗi bước lập luận trong chứng minh bài toán của HS theo mô hình lập luận Toulmin. Trong phân tích lập luận chúng tôi kí

hiệu Di, Ci và Wi lần lượt là các luận cứ, kết luận và luận chứng.

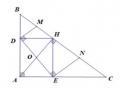
Ví dụ 1.11 Cho tam giác ABC vuông tại A, đường cao AH chia cạnh huyền BC thành hai đoạn BH, CH có độ dài lần lượt là 4cm và 9cm. Gọi D và E lần lượt là hình chiếu của H trên AB và AC.

a, Tính độ dài DE.

b, Các đường thẳng vuông góc với DE tại D và E lần lượt cắt BC tại M và N.

Chứng minh M là trung điểm của BH, N là trung điểm của CH.