Biểuđồ Mứcchênhlệchgiữaphânphốichuẩnvà Student

Hàm NORM.DIST

X: cận của vùng tính xác suất

P X x 

Mean: kỳ vọng  

Standard_dev: độ lệch chuẩn s Cumulative: bằng 0 nếu là hàm mật độ, bằng 1 nếu là hàm phân phối.

Hàm NORM.INV

Probability : giá trị xác suất tính từ

đến cận cần tìm p P X x 

Tính chất. Hàm Laplace  x có các tính chất:

i.  x  x .

ii.  0.5 và  0.5

iii.Nếu Z ~ N 0;1thìP aZ b b a

iv. Nếu

X ~ N ;





thì Z 

X 



~ N 0;1 và P a X b 









b 





a 















Ví dụ 2.18

Cho biến ngẫu nhiên X ~ N 0;1; tính các xác suất.

a. P 1 X 2

b. P 1.5 X 

Giải. Theo tính chất iii

P1 X 2 2 1 2 10.4772 0.3413 0.8185

P 1.5 X P 1.5 X   1.50.5 0.4332 0.0668

Ví dụ 2.19 Điểm Toeic của sinh viên sắp tốt nghiệp ở trường đại học có phân phối chuẩn với giá trị trung bình 560 và độ lệch chuẩn 78. Tính:

a. Tỷ lệ sinh viên có điểm nằm giữa 600 và 700.

b. Tỷ lệ sinh viên có điểm Toeic trên 500.

c. Giả sử nhà trường muốn xác định điểm Toeic tối thiểu để sinh viên có thể ra trường với tỉ lệ 80%. Tính điểm Toeic tối thiểu (lấy phần nguyên).

Giải. Gọi X là điểm Toeic của sinh viên sắp tốt nghiệp,

a. Tỷ lệ sinh viên có điểm nằm giữa 600 và 700

P 600 X 700 700 560 500 560

78

78 



 1.79 0.510.4633 0.1950 0.2683

b. Gọi k là đểm Toeic của sinh viên có thể ra trường. Theo giả thiết

P500X P 500X  560 500560













  0.770.50 0.2794 0.2206

c. Gọi k là điểm Toeic của sinh viên có thể ra trường. Theo giả thiết

P k X 0.8   k560 0.8  k 560 0.3

















Tra bảng B.2 ta được k 560 0.84 vậy k 494 .

Ví dụ 2.20 Đối với người đi vay có điểm tính dụng tốt, nợ trung bình của các tài khoản trả dần và tài khoản trả góp là 15 015 USD (Business Week, 20/3/2006). Giả sử độ lệch chuẩn là 3 540 USD và tiền nợ có phân phối chuẩn.

a. Xác suất để tiền nợ của người vay có điểm tín dụng tốt được lựa chọn ngẫu nhiên cao hơn 18

000 USD là bao nhiêu?

b. Xác suất để tiền nợ của người vay có điểm tín dụng tốt được lựa chọn ngẫu nhiên thấp hơn

10 000 USD là bao nhiêu?

c. Xác suất để tiền nợ của người vay có điểm tín dụng tốt được lựa chọn ngẫu nhiên nằm giữa 12 000 USD và 18 000 USD là bao nhiêu?

d. Xác suất để tiền nợ của người vay có điểm tín dụng tốt được lựa chọn ngẫu nhiên không cao

hơn 14 000 USD là bao nhiêu?

Giải.

Gọi X là tiền nợ của người đi vay có điểm tín dụng tốt. X ~ N 15015; 35402 

a. Xác suất để tiền nợ của người vay có điểm tín dụng tốt được lựa chọn ngẫu nhiên cao hơn 18

000 USD là bao nhiêu?

P X 180000.5  18000 15015 0.5  0.840.5 0.2996 0.2004

3540 



b. Xác suất để tiền nợ của người vay có điểm tín dụng tốt được lựa chọn ngẫu nhiên thấp hơn

10 000 USD là bao nhiêu?

P X 10000 10000 15015 0.5  1.420.5 0.4222 0.5 0.0778

3540 



c. Xác suất để tiền nợ của người vay có điểm tín dụng tốt được lựa chọn ngẫu nhiên nằm giữa 12 000 USD và 18 000 USD là bao nhiêu?

P 12000 X 18000 18000 15015 12000 15015

3540 3540 



 0.84 0.850.2996 0.3023 0.6019

d. Xác suất để tiền nợ của người vay có điểm tín dụng tốt được lựa chọn ngẫu nhiên không cao

hơn 14 000 USD là bao nhiêu?

P X 14000 14000 15015 0.5  0.290.5 0.1141 0.5 0.3859

3540 



2.5 Phân phối Chi bình phương

Định nghĩa (Phân phối Chi bình phương). Cho các biến ngẫu nhiên X1,..., Xnđộc lập cùng

phân phối chuẩn tắc, X ~ N 0;1 . Biến ngẫu nhiên  X X





2 2

được gọi là có phân

phối Chi - bình phương với n - bậc tự do , ký hiệu  2~  2,n .

Với

 2được định nghĩa như trên, ta tìm được hàm mật độ của

 2 . Trước hết ta nhận xét

P X 2 x 0 với mọi x 0 . Nếu x 0 thì hàm phân phối xác suất của X 2 là

1 1

P X 2 x P X x F x F x (*)

Trong đó F là hàm phân phối của biến ngẫu nhiên có phân phối chuẩn tắc. Lấy đạo hàm

hai vế c ủa (*), ta nhận được biể u t hứ c hàm mật độ của 2 là

1 1 x2 

1 2 



2





x 2 e

khi x 0

khi x 0

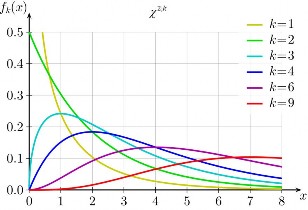
Hình 2.9: Hàm

f x của

X ~  2;k k 1 ; 2 ; 3; 4 ; 6 ; 9

Định lý (Các đặc trưng của phân phối Chi bình phương). Nếu biến ngẫu nhi ên  2~  2,n

thì

i. Kỳ vọng EX n

ii. Phương sai VarX 2n

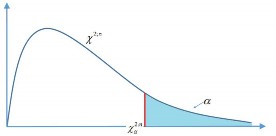
Hình 2.10: Hàm

f x của

X ~  2;n

Tra bảng B4 phần phụ lục bảng tra phân phối Chi Bình Phương.

…	0.995	0.01	0.99	0.015	0.985	…
…	…	…	…	…	…	…	…
7	…	0.9893	18.4753	1.239	17.3984	1.4184	…
8	…	1.3444	20.0902	1.6465	18.9739	1.8603	…
9	…	1.7349	21.666	2.0879	20.5125	2.3349	…
10	…	2.1559	23.2093	2.5582	22.0206	2.8372	…
11	…	2.6032	24.725	3.0535	23.5028	3.3634	…

Có thể bạn quan tâm!

Xem toàn bộ 142 trang tài liệu này.

0.01

Dòng là bậc tự do n và cột là xác suất ở đuôi (phải) của quy luật phân phối

Ví dụ 2.21

 ~  2;10 , ta có  2;10 23,2093 , nghĩa là P 23,20931% .

Trong EXCEL, phân phối siêu bội được tính bằng lệnh : CHISQ.DIST và CHISQ.INV

Hàm CHISQ.DIST

X : cận vùng xác suất tính từ 0 : P 0  2 x 

Deg_freedom: bậc tự do

n

Cumulative: bằng 0 nếu là hàm mật độ, bằng 1 nếu là hàm phân phối.

Hàm CHISQ.INV

Probability: Xác suất của vùng tính từ 0 đến cận x :

p P 0  2 x 

Ví dụ 2.22 Cho  ~  , tính P  32,8 và 

2 ,15





2,15

0.975

Giải. Tra bảng B.5 ta tìm được : P  2 32.80.995

Và P  27.49 0.975 cho nên  27.4884





2,15

0.975

2.6 Phân phối Student

Định nghĩa (Phân phối Student). Cho X ~ N 0;1;Y ~  2,n và X;Y độc lập. Khi đó biến ngẫu nhiên

T X

được gọi là có phân phối Student với n bậc tự do, ký hiệu T ~T n.

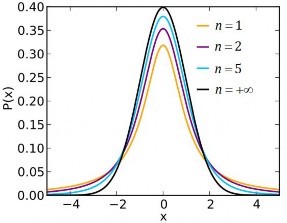
Hình 2.10: Hàm

f x của

X ~T n n 1 ; 2 ; 5; 

Bây giờ ta đi tìm hàm mật độ của biến ngẫu nhiên T ~T n . Bởi vì X và Y độc lập cho nên

hàm mật độ đồng thời sẽ là

gx; y gXxgYy, với

gX x và

gY y 

lần lượt là hàm

mật độ của các biến ngẫu nhiên X và Y .

x2 y 

1 2 

Thực hiện đổi biến:

gx; y 

2n1/2

2 n

2 



e

W Y Y W

X n







X 

1



T 



y

w

x

w

y

t

x

t

Jacobian của phép đổi biến từ X và Y sang T và W là

1 0

J t w

2 nw n

n 

11t2w

1 2 

2n

Suy ra

f t;w g x t ;w , y t ;w . J 

2n1/2

2 n

2 



we



n 1

n1

2 

t2 2

Vậy hàm mật độ của T :

fT t f t ;w dw 

1 

2

n n 



; x 

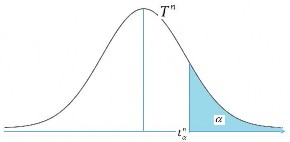
Hình 2.11: Hàm

f x của

X ~T n

Tra bảng B3 phần phụ lục bảng tra phân phối Student:

…	0.015	0.02	0.025	0.03	0.035	…
…	…	…	…	…	…	…	…
7	…	2.7146	2.5168	2.3646	2.2409	2.1365	…
8	…	2.6338	2.449	2.306	2.1892	2.0902	…
9	…	2.5738	2.3984	2.2622	2.1504	2.0554	…
10	…	2.5275	2.3593	2.2281	2.1202	2.0283	…
11	…	2.4907	2.3281	2.201	2.0961	2.0067	…

P T t

Dòng là bậc tự do : n và Cột là xác suất của đuôi (phải) quy luật phân phối.

0,025

Ví dụ 2.23 Cho T ~ T10 , ta có t 10

2,2281 , nghĩa là

0 ,025

2,5% .

Trong EXCEL, phân phối siêu bội được tính bằng lệnh : T.DIST và T.INV

Hàm T.DIST

x : cận vùng xác suất tính từ : P T x 

Deg_freedom: bậc tự do

n

Cumulative: bằng 0 nếu là hàm mật độ, bằng 1 nếu là hàm phân phối.

Hàm T.INV

Probability: vùng xác suất tính từ đến cận x :p P T x 

Giống như phân phối chuẩn tắc, hàm mật độ của biến ngẫu nhiên có phân phối Student đối xứng qua trục tung. Hơn nữa, là khi n càng lớn thì hàm mật độ của T ~T n càng giống với hàm mật độ chuẩn tắc, bởi vì

 2 X 2 ... X 2

1 n

với Xi ,i 1,...,n; là các biến ngẫu nhiên độc lập cùng phân phối chuẩn tắc.

X n

2

Theo định lý luật số lớn 6.10 thì 2P. Cũng từ định lý 6.7 thì T FX

Vậy khi n lớn thì phân phối của biến ngẫu nhiên T ~ Tnđược xấp xỉ bằng phân phối của

biến ngẫu nhiên

X ~ N 0;1;

Nếu gọi

F x ,F x lần lượt là hàm phân phối xác suất của Z ~ N 0;1và T ~ T n . Sai số

1 2

khi ta xấp xỉ phân phối Student bằng phân phối chuẩn tắc

err x F1 x F2 x 

, x 

Sai số lớn nhất sẽ giảm khi n tăng. Sai số lớn nhất là 0,1256 khi n 1 và giảm nhanh đến 0,005244 khi n 30 ; xem hình 5.13.

Khi bậc tự do n 30 ; sai số giữa hai phân phối được mô đánh giá như đồ thị 5.14.

Sai số lớn nhất sẽ giảm khi n tăng lên, sai số lớn nhất là 0,1256 khi n 1 sẽ giảm xuống còn 0,005244 khi n 30 .

Nên trong thực nghiệm, khi n đủ lớn ( n 30) ta có thể xấp xỉ phân phối Student bằng phân phối chuẩn

0.14

0.12

0.1

0.08

0.06

0.04

0.02

0.00 0.20 0.40 0.60 0.80 1.00 1.20 1.40 1.60 1.80 2.00 2.20 2.40 2.60 2.80 3.00 3.20 3.40

cận x

r = 1

r = 10

r = 30

ĐỘ LỆCH HAI PHÂN PHỐI

Hình 2.12: Biểuđồ mứcchênhlệchgiữaphânphốichuẩnvà Student

CHƯƠNG 3 : NGUYÊN LÝ THỐNG KÊ VÀ CÁC KHÁI NIỆM CƠ BẢN41

CHƯƠNG

NGUYÊN LÝ THỐNG KÊ VÀ

CÁC KHÁI NIỆM CƠ BẢN

Mục lục chương 3

3.1 Một số khái niệm dùng trong thống kê 41

3.2 Tổng hợp và trình bày dữ liệu thống kê 47

3.1. Một số khái niệm dùng trong thống kê.

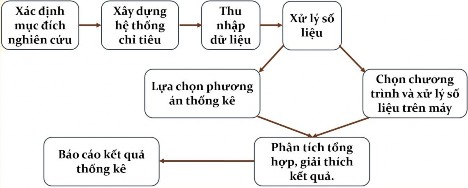
Trong quá trình ứng dụng thống kê để giải quyết các vấn đề, đối với một đối tượng nghiên cứu, vì những lý do thực tế đôi khi ta không thể thu thập toàn bộ dữ liệu, mà ta chỉ nghiên cứu trên một phần, một bộ phận của đối tượng. Do đó dữ liệu thống kê được dùng theo hai mục tiêu là thống kê mô tả và thống kê suy diễn.

Thống kê mô tả: dùng để tóm tắt dữ liệu, mô tả dữ liệu dưới dạng số hay dùng các công cụ đồ họa. Tóm tắt dưới dạng số thường dùng giá trị trung bình, độ lệch chuẩn, trung vị, yếu vị. Công cụ đồ họa thường dùng là biểu đồ và đồ thị.

Thống kê suy diễn: dùng để mô hình hóa các kiểu biến thiên của dữ liệu và rút ra các kết luận cho tổng thể mà ta không có điều kiện để nghiên cứu hết đội tượng mà ta quan tâm. Các kết luận có thể thiên về ước lượng, kiểm định, dự đoán, mô tả mối liên hệ hay mô hình hóa mối liên hệ. Ngoài ra còn các kỹ thuật khác mô hình hóa dữ liệu như: phân tích phương sai, dãy số và chuỗi thời gian và khai thác dữ liệu.

Tổng thể thống kê và đơn vị tổng thể, và mẫu.

Tổng thể thống kê (còn gọi là tổng thể chung) là tập hợp các đơn vị cá biệt (hay phần tử) thuộc hiện tượng nghiên cứu, cần quan sát, thu thập và phân tích mặt lượng của chúng theo một hay