Thuật Toán Hybrids Đàn Kiến Tối Ưu Truy Vấn Phân Tán

Total_cost = LT(gọi card(R) bộ từ R)

+ CT(length(A))*card(R)

+ LT(gọi s bộ từ S)*card(R)

+ CT(s*length(S))*card(R)

+ Chiến lược 4: Chuyển cả hai quan hệ tới trạm thứ ba và tính toán kết nối ở đó. Trường hợp này quan hệ trong trước tiên được chuyển tới trạm thứ 3 và được lưu trong một quan hệ tạm thời T. Sau đó quan hệ ngoài được chuyển đến trạm thứ 3 và các bộ của nó được kết nối với T khi chúng đến. Vì vậy ta có:

Total_cost = LT(gọi card(S) bộ từ S)

+ CT(size(S))

+ LT(gọi card(S) bộ từ T)

+ LT(gọi card(R) bộ từ R)

+ CT(size(R))

+ LT(gọi s bộ từ T)*card(R)

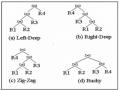
Thuật toán R* giảm đáng kể số các lựa chọn bằng sử dụng quy hoạch động và thực nghiệm. Với quy hoạch động, cây của các lựa chọn được cấu trúc động và được lược bớt bằng cách loại các lựa chọn không có hiệu quả.

Độ phức tạp của thuật toán: Thuật toán này tìm kiếm toàn bộ lấy từ hệ R*. Về mặt thiết kế có thể xem là sự liên hệ n! hoán vị thứ tự các kết nối để từ đó chọn ra hoán vị với chi phí cực tiểu. Độ phức tạp của thuật toán này là tỷ lệ với n! và khiến chi phí cho việc tối ưu hoá lớn khi n lớn.

Ví dụ 2.16: Xét câu truy vấn q1: “Tên của các nhân viên làm dự án CAD/CAM” biểu diễn dưới dạng SQL như sau:

SELECT NV.TenNV FROM NV, PC, DA

WHERE NV.MaNV = PC. MaNV

and PC.MaDA = DA.MaDA

and DA.TenDA = “CAD/CAM”

P

MNV

MDA

N

D

có đồ thị nối như Hình 2.1

sau:

Hình 2.18: Đồ thị nối của truy vấn q1

3 quan hệ được lưu trên 3 trạm khác nhau.

Các bước của thuật toán được minh họa như sau:

- Bước (1): Giả sử chọn được các đường truy cập các quan hệ tốt nhất như

+ NV: Quét tuần tự (vì không có phép chọn nào trên NV)

+ PC: Quét tuần tự (vì không có phép chọn nào trên PC)

+ DA: Chỉ mục trên trường TenDA (do có phép chọn trên DA dựa vào TenDA)

- Bước (2), (3): Xác định các chiến lược kết nối với mỗi thứ tự (tối đa 3! thứ tự):

 PC

DA	NV
 DA	PC	NV
 PC	NV	DA

Có thể bạn quan tâm!

• Rút Gọn Cho Phân Mảnh Ngang Dẫn Xuất
• Đồ Thị Minh Họa Tổng Chi Phí Và Thời Gian Trả Lời
• Tối ưu hóa truy vấn trong các cơ sở dữ liệu phân tán - 8
• Tối ưu hóa truy vấn trong các cơ sở dữ liệu phân tán - 10
• Tối ưu hóa truy vấn trong các cơ sở dữ liệu phân tán - 11
• Tối ưu hóa truy vấn trong các cơ sở dữ liệu phân tán - 12

Xem toàn bộ 103 trang tài liệu này.

 NV x DA PC

 DA x NV PC

Ta có cây chiến lược như Hình 2.19. Mức đầu tiên của cây thể hiện đường truy cập từng quan hệ tốt nhất. Mức thứ 2 thể hiện phương thức kết nối tốt nhất của từng quan hệ với quan hệ khác. Chiến lược NV x DA và DA x NV được tỉa do sử dụng tích đề các được tránh sử dụng (thay thế bởi chiến lược khác). Giả sử NV

PC và PC DA có chi phí cao hơn PC NV và DA PC, do đó chúng được tỉa. Hai khả năng còn lại được thể hiện ở mức độ thứ 3 của cây. Thứ tự kết nối tốt

nhất có chi phí tốt nhất nằm trong một trong 2 chiến lược: (PC NV) DA và (DA PC) NV. Do DA đã được xác định đường truy cập theo chỉ mục trên trường TenDA tốt hơn là quét tuần tự trên PC nên chiến lược (DA PC) NV sẽ được lựa chọn là chiến lược có chi phí tốt nhất để thực thi câu truy vấn. Cụ thể là: Chọn trên quan hệ DA theo chỉ mục TenDA  kết nối với quan hệ PC theo chỉ mục MDA  kết nối với NV theo chỉ mục MNV.

- Bước (4): Việc truyền dữ liệu giữa các trạm sử dụng một trong hai kỹ thuật Ship-whole hoặc Fetch – as – needed được trình bày ở trên dựa vào lực lượng của từng quan hệ và của quan hệ trung gian.

NV

PC

DA

NV PC

NV x DA

PC

PC

DA

Tỉa

DA

PC

DA x NV

(PC

NV)

DA

(DA

PC)

NV

Hình 2.19: Các thứ tự kết nối

2.4.3. Thuật toán SDD-1

Thuật toán tối ưu hóa truy vấn SDD-1 xuất phát từ giải thuật “leo dốc”, thuật toán này thực hiện chọn một giải pháp có thể thực thi ban đầu và lặp đi lặp lại để cải tiến nó cho đến khi đạt tới đích.

Thuật toán sử dụng phép nửa kết nối, hàm mục tiêu tối thiểu chi phí truyền thông (chi phí địa phương và thời gian đáp không được xét), thuật toán sử dụng các thống kê trên cơ sở dữ liệu, được gọi là hồ sơ cơ sở dữ liệu, một hồ sơ gắn với một quan hệ. Về cơ bản thuật toán đầu tiên chọn một chiến lược thực hiện mềm dẻo mà được xác định một cách lặp. Sau đó sử dụng các phép tối ưu hóa sau

(posttimization) để cải tiến tổng chi phí của chiến lược được chọn. Bước chính của thuật toán gồm việc xác định và sắp thứ tự các phép nửa kết nối có chi phí nhỏ hơn lợi ích của nó.

Để chọn ra phép nửa kết nối hiệu quả, thuật toán sử dụng các đánh giá về chi phí và lợi ích được xác định như sau:

Chi phí của phép nửa kết nối:

( ⋉A S) = CMSG + CTR * size(πA(S)) Đánh giá về lợi ích:

Benefit(R⋉AS) = (1-SFSJ(S.A))*size (R)*CTR

Thuật toán SDD-1 nhận đầu vào là một đồ thị truy vấn với n quan hệ, các thống kê cơ sở dữ liệu của mỗi quan hệ. Đầu ra của thuật toán là một chiến lược tổng thể để thực thi truy vấn. Giải thuật tiến hành theo bốn giai đoạn: khởi đầu, chọn các phép toán nửa kết nối có lợi, chọn trạm thực hiện và tối ưu hóa sau, được trình bày bởi thuật toán SDD-1 sau:

Thuật toán SDD-1

Input: QG: Đồ thị truy vấn với n quan hệ, các hệ thống kê của mỗi quan hệ

Output: ES: Chiến lược thực hiện.

Begin

ES  local-operation(QG);

Sửa đổi các thống kê để phản ánh các kết quả xử lý địa phương BS  {tập các phép nửa kết nối có lợi}

for mỗi phép kết nối SJ trong QG do If cost(SJ) < benefit(SJ) then

BS  BS I  SJ

end-if end-for

while BS ≠ do {Chọn các phép nửa kết nối có lợi}

begin

SJ  most_beneficial (BS) {SJ: nửa kết nối với benefit-cost lớn nhất} BS  BS - SJ {loại SJ khỏi BS}

ES  BS + SJ {bổ sung SJ vào chiến lược thực thi ES} Sửa đổi thống kê để phản ánh kết quả của SJ thêm vào

BS  BS – các phép nửa kết nối không có lợi BS  BS  các phép nửa kết nối có lợi mới

end-while

{Chọn trạm thực hiện}

AS(ES)  chọn trạm i mà i chứa số lượng dữ liệu lớn nhất sau tất cả các phép toán cục bộ

ES  ES  sự truyền của các quan hệ trung gian tới AS(ES) {tối ưu hóa sau}

for mỗi quan hệ Ri tại AS(ES) do

for mỗi phép nửa kết nối SJ của Ri với Rj do if cost(ES) > cost(ES – SJ) then

ES  ES – SJ

end-if end-for

end-for

End. {Thuật toán SDD – 1}

1) Giai đoạn khởi đầu: Sinh ra một tập các phép nửa kết nối có lợi.

BS = {SJ1,…SJn} và một chiến lược thực thi (ES) bao gồm các xử lý địa phương.

2) Giai đoạn hai: Lặp lại lựa chọn ra các phép kết nối có lợi nhất (SJi) từ BS, sửa đổi các thống kê cơ sở dữ liệu và BS. Sự sửa đổi ảnh hưởng đến hệ R. Vòng lặp kết thúc khi tất cả các phép nửa kết nối trong BS đã được thêm vào ES sẽ là thứ tự thực hiện của chúng.

3) Giai đoạn chọn các trạm thực hiện: Với mỗi trạm đề cử, đánh giá chi phí truyền tất cả dữ liệu được yêu cầu tới nó và chọn trạm có chi phí nhỏ nhất.

4) Giai đoạn tối ưu hóa sau: Loại bỏ những phép kết nối trong chiến lược thực thi chỉ ảnh hưởng đến quan hệ được lưu tại trạm thực hiện. Bộ tối ưu hóa SDD-1 dựa trên thừa nhận các quan hệ có thể được truyền tới trạm khác. Điều này đúng cho tất cả các quan hệ loại trừ những quan hệ thuộc trạm thực hiện, mà chúng được chọn sau khi các phép nửa kết nối có lợi được xem xét. Vì vậy, một số phép nửa kết nối không có lợi bước tối ưu hóa truy vấn sau loại chúng khỏi chiến lược thực hiện.

Ví dụ 2.16: Xét truy vấn SELECT *

FROM E, G, J

WHERE E.MANV = G.MANV AND G.MANV = J.MANV

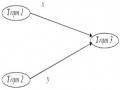
Hình 2.20 đưa ra đồ thị kết nối của truy vấn và thống kê quan hệ. Giả sử CMSG = 0 và CTR = 1

Quan hệ

Lực lượng	Kích thước bộ	Kích thước quan hệ
E	30	50	1500
J	100	30	3000
G	50	40	2000

Thuộc tính

SFSJ	Kích thước (πATRI)
E.MANV	0.3	120
G.MANV	0.8	400
G.MANV	1	400
J.MANV	0.4	200

Bảng: Truy vấn ví dụ và thống kê

Các phép kết nối có lợi ban đầu như sau:

SJ1: G E, lợi ích là 2100 = (1 - 0.3) * 3000 và chi phí là 120 SJ2: G J, lợi ích là 1800 = (1 - 0.4) * 3000 và chi phí là 200

Hai phép kết nối không có lợi là:

SJ3: E G, lợi ích là 300 = (1 - 0.8) * 1500 và chi phí là 400 SJ4: J G, lợi ích là 0 và chi phí là 400

Tại bước lặp đầu tiên, SJ1 được thêm vào chiến lược thực hiện ES. Kích thước của G thay đổi thành 360 = 1500 * 0.24); SFSJ = (E.ENO) thay đổi.

Tại bước lặp thứ ba, phép nửa kết nối còn lại là SJ2 được thêm vào ES. Kích thước của G thay đổi thành 360 = 900 * 0.4; SFSJ(G.JNO) thay đổi.

Sau khi rút gọn, số lượng dữ liệu lưu tại trạm 1 là 360, trạm 2 là 360, trạm 3 là 2000. Vì vậy trạm 3 được chọn làm trạm thực hiện. Bước tối ưu hóa sau không bỏ bất cứ phép nửa kết nối vì chúng đều có lợi. Chiến lược được chọn là gửi (E G) J và (E G) tới trạm 3, tại đó kết quả cuối cùng được tính toán.

2.4.4. Thuật toán Hybrids đàn kiến tối ưu truy vấn phân tán

Dựa trên ưu điểm, nhược điểm của 2 thuật toán quy hoạch động và tối ưu đàn kiến, Tansel và cộng sự đã đề xuất thuật toán DP-ACO để tối ưu hóa truy vấn đa kết nối bằng (multi way chain equijoin queries) trong môi trường CSDL phân tán. Quy hoạch động tạo ra những thiết kế tốt nhất có thể nhưng có thời gian thực hiện dài và yêu cầu bộ nhớ rất lớn khi kích thước của các quan hệ và số lượng kết nối tăng lên trong truy vấn. Quy hoạch động có thể thực hiện tối ưu đến 7 quan hệ nhưng DP-ACO đã được chứng minh là giải pháp khả thi bằng việc tạo ra các kế hoạch thực thi tốt với các câu truy vấn 15 quan hệ trong thời gian giới hạn và không gian bộ nhớ hạn chế. Một ưu điểm khác của DP-ACO là có thể dễ dàng thích ứng với bộ tối ưu hóa truy vấn đang tồn tại sử dụng thuật toán dựa trên quy hoạch động.

 Thuật toán tối ưu đàn kiến (ACO Metaheuristic) [7]

Thuật toán dựa trên hành vi của đàn kiến thực trong việc thiết lập đường đi ngắn nhất giữa thức ăn và tổ của nó. Kiến có thể giao tiếp với nhau thông qua các hóa chất phát ra từ chúng trên đường đi từ tổ tới chỗ thức ăn và ngược lại, gọi là pheromone. Như vậy, đường đi ngắn hơn là đường có lượng pheromone cao hơn, kiến sẽ có xu hướng chọn con đường ngắn hơn này.

Thuật toán tối ưu đàn kiến: Hình 2.21 mô tả quy trình ra quyết định của loài kiến trong việc lựa chọn đường đi của chúng. Khi các con kiến gặp nhau ở điểm ra quyết định A, một số sẽ lựa chọn đi theo hướng này và một số chọn đi theo hướng khác một cách ngẫu nhiên. Giả sử kiến có tốc độ di chuyển như nhau, những con lựa chọn bên ngắn sẽ đến B nhanh hơn so với những con chọn bên còn lại. Kết quả là lượng pheromone sẽ lớn hơn ở bên ngắn so với bên dài do nhiều kiến chọn hơn. Hệ thống đàn kiến nhân tạo được tạo thành từ nguyên tắc này của đàn kiến để giải quyết các vấn đề tối ưu hóa khác nhau. Pheromone là chìa khóa ra quyết định của đàn kiến.

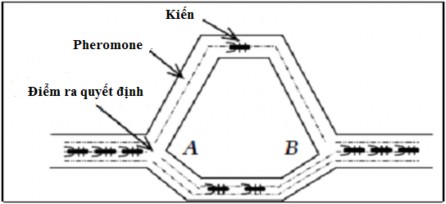
Hình 2.20: Quá trình quyết định đường đi của đàn kiến

Trong ACO, một con kiến nhân tạo sẽ xây dựng giải pháp bằng cách đi qua đồ thị kết nối đầy đủ GC(V,E), trong đó V là tập các đỉnh, E là tập các cạnh. Theo Dorigo, kiến nhân tạo sẽ di chuyển từ đỉnh tới đỉnh dọc theo các cạnh của đồ thị để xây dựng giải pháp thành phần (partial solution). Thuật toán tối ưu hóa đàn kiến đầu tiên được biết đến là Ant System, được đề xuất từ những năm 90. Sau đó, một số thuật toán ACO khác đã được đề xuất. Hình 2.21 mô tả thuật toán ACO metaheuristic, lặp 3 giai đoạn: