N I N N

phối nhị thức.

a. Tính xác suất có 2 sinh viên có mức dư nợ thẻ tín dụng cao hơn 7000 USD.

Cần tính P X 2

P X 2 C 0.09 1 0.09 0.1714





2





2



8

10

b. Tính xác suất không có sinh viên nào có mức dư nợ thẻ tín dụng cao hơn 7000 USD.

P X 0 C 0.09 1 0.09 0.3894





0

10





0



10

c. Tính xác suất có ít nhất 3 sinh viên có mức dư nợ thẻ tín dụng cao hơn 7000 USD.

PX3P 3X 101 PX0P X1P X20.9460

2.2 Phân phối siêu bội

Định nghĩa (phân phối siêu bội) một tập gồm có N phần tử, trong đó có NA phần tử có

tính chất A và N — NA phần tử không có tính chất A. Từ tập ta lấy ngẫu nhiên n phần tử (lấy một lần n phần tử hoặc lấy n lần không hoàn lại mỗi lần một phần tử).

Gọi X là số phần tử có tính chất A lẫn trong n phần tử lấy ra từ tập . Khi đó X là biến

ngẫu nhiên rời rạc nhận giá trị k sao cho 0k n

n N NAk NA

P X k NA N NA; k S

Ck Cnk

Cn

N

Biến ngẫu nhiên rời rạc X được gọi là có phân phối siêu bội với tham số N; NA; n, ký hiệu X ~ H N;NA;n

Ví dụ 2.8 Siêu thị mở đợt khuyến mãi dành cho khách hàng mua 5 sản phẩm từ một lô hàng gồm 15 sản phẩm trong đó có 5 sản phẩm loại A và 10 sản phẩm loại B. Quản lý muốn quan tâm về số lượng sản phẩm mà khách hàng mua như sau

a. Trong 5 sản phẩm khách hàng chọn, xác suất có 3 sản phẩm loại A là bao nhiêu.

b. Trung bình có bao nhiêu sản phẩm loại A mà khách hàng sẽ mua trong 5 sản phẩm.

c. Độ lệch chuẩn về số sản phẩm A mà khách hàng mua trong 5 sản phẩm.

d. Số sản phẩm A chắc chắn nhất mà khách hàng sẽ mua trong 5 sản phẩm.

Ví dụ 2.9 Bộ phận marketing của một dooanh nghiệp có 50 nhân viên trong đó có 30 nhân viên nữ. Cần chọn 10 nhân viên tiếp thị cho một sản phẩm mới, giả sử khả năng được chọn của các nhân viên là như nhau. Gọi X là số nhân viên nữ được chọn. Tính xác suất có

a. Không quá 3 nhân viên nữ được chọn.

b. Ít nhất một nhân viên nữ được chọn

Giải. X là số nhân viên nữ được chọn, khi đó X ~ H 50;30;10

a. Xác suất không quá 3 nhân viên nữ được chọn :

P X 3P X 0P X 1P X 2P X 3

C 0 C10 C 1 C 9 C 2 C 8 C 3 C 7

30 2030 2030 2030 200.03648

C 10 C10 C 10 C 0

50 50 50 50

b. Xác suất ít nhất một nhân viên nữ được chọn :

C C

0 10

C

10

P X 11 P X 11 P X 01 30 200.99998

50

BNN	MẬT ĐỘ	PHÂN PHỐI
0	1.799E-05	1.799E-05
1	0.0004905	0.0005085
2	0.0053344	0.005843
3	0.0306389	0.0364818
4	0.1034063	0.1398881
5	0.215085	0.3549731
6	0.2800586	0.6350317
7	0.2259296	0.8609613
8	0.1082579	0.9692193
9	0.0278558	0.9970751
10	0.0029249	1

Có thể bạn quan tâm!

• Thống kê ứng dụng trong kinh tế và kinh doanh - Trường ĐH Văn Lang - 2
• Nếu X Là Biến Ngẫu Nhiên Rời Rạc Có Bảng Phân Phối Xác Suất Cho Bởi
• Nếu X Và Y Độc Lập Thì Var X  Y   Varx  Vary
• Biểuđồ Mứcchênhlệchgiữaphânphốichuẩnvà Student
• Tiêu Thức Bất Biến Và Tiêu Thức Biến Động.
• Các Đại Lượng Đo Lường Mức Độ Tập Trung Của Dữ Liệu 55

Xem toàn bộ 142 trang tài liệu này.

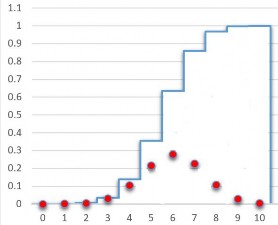
Hình 2.4: Hàm

f x và F x của

X ~ H 50;30;10

Định lý. Trong mô hình phân phối siêu bội, khi thực hiện phép thử ta lấy liên tiếp n

lần không hoàn lại, mỗi lần lấy một phần tử. Ta gọi

X 1 nếu lần i lấy được phần tử loại A .

i



0 nếu lần i không lấy được phần tử loại A.

i. Xác suất mỗi lần lấy phần tử A là như nhau, nghĩa là

P X 1 ; i 1,...,n





N

A

i

N

ii. Với mọi i j thì

P X 1; X 1 



N N 1

i

j



A A

N N 1

Chứng minh: Đặt các biến

Ai : “ trong n lần đầu có i phần tử loại A”, i 1, ...,n

i. Xác suất lần n+1 lấy được phần tử loại A là

P Xn1 1P A0P Xk1 A| A0... P AnP Xk1 1| An

n N k

C k C nk

1 n n 

A.N A N N A

N C k C nk

kC k C nk 

k 0 N n C n N nC n 

A NA

k 0

N NA

k 0

NA N NA 

N N

1 N C n 

n

N



N

k A C k 1 C nk A

n1

N 





n C k 1 C n1k 1

N 

N nC n A N



k 1

k NA 1

N NA 



N nC n CN



k 1

NA 1

N 1N A 1



NA

Cn C n1 NA

Cn n C n NA

1 n NA

N nC n

N N 1

N nC n N

N N 

N n

N N

N N 

ii. Không mất tính tổng quát, ta giả sử j > i

P X

1; X 1P X 1P X 1| X

1NA . NA 1

i j i j i

N N 1

Nhận xét : Ta thấy biến ngẫu nhiên Xi

~ B NA nên kỳ vọng và phương sai

N 



EX NA ; Var X NA . N NA

i N i N N

Kỳ vọng của tích E X X P X 1; X

1NA . NA 1

i j i j

N N 1

N 2

N

Và tích của hai kỳ vọng EXi .EX j A



Hiệp phương sai

Cov Xi; X jE XiX jEXi.EX j

N N 1 N 2

N N N 

A AA

A A

N N 1

N 

N2 N 1

Định lý (Các đặc trưng của biến ngẫu nhiên siêu bội). Nếu biến ngẫu nhiên

X~ H N;NA;nthì

i. Kỳ vọng EX np với p NA

N

ii. Phương sai VarX npq N n với q 1 p

N 1

iii. Giá trị Mod với n1NA11 ModX n1NA1

N 2

N 2

Chứng minh.

i. Ta có X X

1 X2

... Xn

nên EX EX

1 EX2

... EXn

n NA

N

ii. Khai triển phương sai cho biểu thức:

Var n

XnVar X2Cov X; X

n NA . N NA 2C 2 N N NA 

i 

i 1

i

i 1

i j

i j N N

n N2 n 1



n NA . N NA n 1n N N NA n NA . N NA 1 n 1

N N N2 n 1N N N 1 





n NA . N NA .N n 

N N N 1 

iii. Gọi Pk P X k ; xét tỷ số

Pk P Xk NAk 1nk 1

Pk 1

P X k 1

k N NA n k 

suy ra P là dãy tăng khi và chỉ khi k n1NA1k

k N 2 0

và là dãy không giảm khi và chỉ khi k k0

Khi k0

không là số nguyên. k ModX

là số nguyên lớn nhất nhỏ hơn k0 :

n 1NA11 ModX n 1NA1

N 2 N 2

Khi k0 là số nguyên. Ta có ngay ModX k0 k vì khi k k0 thì Pk là dãy không giảm.

Mặc khác, lúc này nên Pk Pk 1 cũng là ModX :

n 1NA11 ModX n 1NA1

N 2

Từ hai trường hợp trên suy ra

N 2

n 1NA11 ModX n 1NA1

N 2 N 2

Ví dụ 2.10 Có một cái hộp chứa 8 quả cầu trắng và 3 quả cầu đen. Lấy ngẫu nhiên không hoàn lại 4 quả cầu. Gọi X là số quả cầu trắng lấy được. Tính xác suất

a. Lấy được ít nhất 1 quả cầu trắng.

b. Lấy được 2 quả cầu trắng.

c. Tính EX và VarX .

Giải. X là số bi trắng lẫn trong 4 bi lấy ra, X ~ H 11;8;4.

a. P X 11

C

P X 28 3

4

b. C2C2 14

11 15

c. Kỳ vọng EX np 4. 8 32

11 11

Phương sai VarX npq N n 4. 8 . 3 . 7

336

N 1 11 11 10 605

Trong EXCEL, phân phối siêu bội được tính bằng lệnh : HYPGEOM.DIST

Sample_s : là số phần tử thỏa A

được lấy ra k Number_sample : là số phần tử lấy ra n

Population_s : là số phần tử thỏa A có trong tập hợp. NANumber_pop : là tổng số phần tử có trong tập hợp N Cumulative : bằng 0 nếu là hàm mật độ và bằng 1 nếu là hàm phân phối

Ví dụ 2.11 : X ~ H 50;30;10

P X 50,3550

Ví dụ 2.12 Trong một cuộc khảo sát được thực hiện bởi Tổ chức Gallup, người tham gia được hỏi: “Bạn thích môn thể thao nào?” Bóng đã Mỹ và bóng rổ xếp hạng nhất và hạng hai về sở thích (www.gallup.com, ngày 03/01/2004). Giả sử rằng trong một nhóm 10 người, bảy người thích bóng đá và ba người thích bóng rổ. Xét một mẫu ngẫu nhiên gồm 3 trong số 10 người trên.

a. Xác suất có đúng 2 người thích bóng đá là bao nhiêu?

P X 27 30.525

C2C1

C3

10

b. Xác suất mà phần lớn (hai hay ba người) thích bóng đá là bao nhiêu?

C2C1 C3C 0

P X 2P x 2P X 37 37 30.8176

C 3 C 3

10 10

2.3 Phân phối Poisson

Trong phần này ta xét biến ngẫu nhiên rời rạc thường dùng để ước lượng số lần xảy ra trong một khoảng thời gian hoặc không gian nhất định.

Ví dụ 2.13 Biến ngẫu nhiên chỉ số ôtô đến một cửa hàng rửa xe trong một một giờ, số hư

hỏng cần sửa chửa trên 10 dặm đường cao tốc, hoặc số lỗ lủng trên 100m ống dẫn nước. Tính chất của phép thử Poisson:

1. Đối với hai khoảng bất kỳ có độ dài bằng nhau thì xác suất xảy ra bằng nhau.

2. Việc xuất hiện hoặc không xuất hiện trong khoảng này độc lập với trong khoảng khác.

Định nghĩa (Phân phối Poisson). Biến ngẫu nhiên rời rạc X nhận giá trị nguyên dương

k 0,1,2,... với xác suất

P X k 

k e

k!

; k 0,1,2,...

được gọi là có phân phối Poisson với tham số  , ký hiệu X ~ P  .

Ví dụ 2.14 Tại một trường đại học mở một khóa học, và học viên đăng ký qua điện thoại, theo kinh nghiệm trong những đợt ghi danh trước thì trung bình cứ 2 phút có 1 cuộc gọi đến. Để đạt hiệu quả cao trong việc tiếp học viên, quản lý phòng ghi danh cần quan tâm đến việc bố trí nhân viên trực phù hợp thông qua các vấn đề

a. Xác suất có 5 học viên gọi đến trong 10 phút.

b. Trung bình có bao nhiêu học viên gọi đến trong 10 phút.

c. Độ lệch chuẩn về số lượng học viên gọi đến trong 10 phút.

d. Số lượng học viên gọi điện đến chắc chắn nhất trong 10 phút là bao nhiêu.

Ví dụ 2.15 Tại một nhà máy dệt, trung bình có 8 ống sợi bị đứt trong hai giờ. Tìm xác suất để trong một giờ có không quá 2 ống sợi bị đứt.

Giải. Gọi X là số ống sợi bị đứt trong một giờ, X ~ P 4. Ta cần tìm xác suất

4 e 4 e 4 e

0 4 1 4 2 4

P X 2P X 0P X 1P X 213e4

BNN	MẬT ĐỘ
0	0.0183156
1	0.0732626
2	0.1465251
3	0.1953668
….	….
12	0.0006415
13	0.0001974
14	5.64E-05
15	1.504E-05

0! 1! 2!

0.25

0.2

0.15

0.1

0.05

0

0

5

10

15

Hình 2.4: Hàm

f x của

X ~ P 4

Định lý (Các đặc trưng của biến ngẫu nhiên phân phối Poisson). Nếu biến ngẫu nhiên X có phân phối Poisson với tham số  , X ~ P  thì:

i. Kỳ vọng EX  .

ii. Phương sai VarX  .

iii.  1 ModX 

Ví dụ 2.16 Ở một tổng đài điện thoại, trung bình có 50 cuộc gọi đến trong 5 phút. Tìm xác suất để trong 1 phút:

a. Có đúng 5 cuộc gọi đến trong 1 phút.

b. Có ít nhất 2 cuộc gọi trong 1 phút.

Giải. Trung bình trong một phút có 10 cuộc gọi đến. Gọi X là số cuộc gọi đến tổng đài trong 1 phút thì X ~ P 10

a. Xác suất có đúng 5 cuộc gọi đến trong 1 phút.

5 10

P X 510 e

5!

0.0378

b. Xác suất có ít nhất 2 cuộc gọi đến trong một phút.

PX21 P X21 P X11 P X0P X10.9995

Ví dụ 2.17 Tại một trường đại học đăng ký khóa học bằng điện thoại, trung bình có 1 cuộc gọi đến trong 2 phút.

a. Số cuộc gọi kỳ vọng trong một giờ là bao nhiêu?

b. Xác suất có 3 cuộc gọi trong vòng 5 phút là bao nhiêu?

c. Xác suất không có cuộc gọi nào trong một khoảng thời gian là 5 phút là bao nhiêu?

Giải.

a. Vì trung bình có 1 cuộc gọi đến trong 2 phút nên có 30 cuộc gọi đến trong một giờ (60 phút)

b. Xác suất có 3 cuộc gọi trong vòng 5 phút là bao nhiêu?

e10 103

P X 3

với X là số cuộc gọi đến trong 5 phút

c. Xác suất không có cuộc gọi nào trong một khoảng thời gian là 5 phút là bao nhiêu?

3!

0,0076

P X 0e

10 0

10

0!

4.5410 .

5

1

 2

2.4 Phân phối chuẩn

Định nghĩa (Phân phối chuẩn). Biến ngẫu nhiên lên tục X nhận giá trị trong khoảng

;được gọi là có phân phối chuẩn tham số  , 0 . Ký hiệu X ~ N  , 2nếu hàm

mật độ xác suất có dạng

fx



x  2



e 



2

2

x 

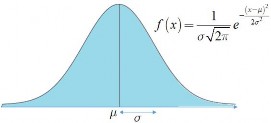
Nhận xét

Hình 2.5: Hàm

f x của

X ~ N ; 2 

 2 

Hàm mật độ chuẩn dạng hình chuông đối xứng qua x  và giá trị cực đại 1

tại x 

Hình 2.6 là đồ thị của biến ngẫu nhiên chuẩn khi cố định

 0 , thay đổi giá trị của

  20.2;1;5. Đồ thị hàm mật độ của biến ngẫu nhiên chuẩn với  20.2 sẽ cao hơn

và ít phân tán xung quanh giá trị trung bình hơn so với các trường hợp phương sai lớn

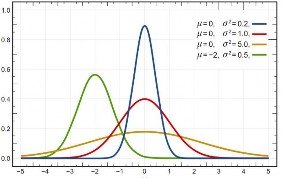
hơn.

Hình 2.6: Hàm

f x của

X ~ N ; 2 

Định lý (Các đặc trưng của biến ngẫu nhiên chuẩn). Nếu X là biến ngẫu nhiên có

phân phối chuẩn tham số ; thì

i. EX  và VarX  2

ii. ModX 

1

2

Định nghĩa (Phân phối chuẩn tắc). Biến ngẫu nhiên Z có phân phối chuẩn với tham số  0 và  2 1 được gọi là có phân phối chuẩn tắc, ký hiệu Z ~ N 0;1Hàm mật độ của Z ~ N 0;1

f z 

z2



e





2

, z 

Đồ thị hàm mật độ biến ngẫu nhiên chuẩn tắc Z ~ N 0;1đối xứng qua trục tung,

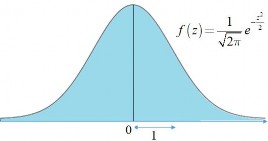
Hình 2.7: Hàm

f x của

X ~ N 0;1

x

Định nghĩa (Hàm Laplace). Cho Z ~ N 0;1. Đặt  xfzdz , 0 x gọi là hàm

0

Laplace (Giá trị  x được tính sẵn trong bảng B.2 phần phụ lục)

z	0.00 0.01 0.02 0.06 0.07 0.08 0.09
…
1.7
1.8
1.9
2.0
2.1
…

…	…	…	…	…	…	…	…
0.4554	0.4564	0.4573	…	0.4608	0.4616	0.4625	0.4633
0.4641	0.4649	0.4656	…	0.4686	0.4693	0.4699	0.4706
0.4713	0.4719	0.4726	…	0.4750	0.4756	0.4761	0.4767
0.4772	0.4778	0.4783	…	0.4803	0.4808	0.4812	0.4817
0.4821	0.4826	0.4830	,,,	0.4846	0.4850	0.4854	0.4857
…	…	…	..,,	…	…	…	…

Hình 2.8: Hàm Laplace  x

Đối với bảng tra B2 thì đo vùng xác suất  x từ 0 đến cận x . Tức nếu biết cận thì sẽ tìm được vùng xác suất và ngược lại.

Ví dụ :  1,960,475 , tức vùng xác suất từ 0 đến 1,96 trong quy luật phân phối chuẩn đơn giản

bằng 0,475.

Đối với bảng tra trong Excel ta dùng 2 lệnh sau:

NORMSDIST(z) : đo vùng xác suất tới cận z trong quy luật phân phối chuẩn.

Ví dụ: Trong excel NORMSDIST 1,960,975 , ta có thể hiểu chênh lệch với kết quả trong bảng tra là 0,5; là vùng xác suất từ đến 0.

NORMSINV(probability) : đo cận tương tứng với vùng xác suất tính từ .

Ví dụ: Trong excel NORMSINV (0, 975) 1,96

Nếu ta cần làm việc với phân phối chuẩn tổng quát, trong EXCEL có 2 hàm sau: