Nếu X Và Y Độc Lập Thì Var X  Y   Varx  Vary

i. Var C 0

ii. Var CX C 2VarX

iii. Nếu X và Y độc lập thì Var X Y VarX VarY

y67hg

III. Độ lệch chuẩn.

Do cách xây dựng công thức tính phương sai của biến ngẫu nhiên mà đơn vị đo của phương sai bằng bình phương đơn vị đo của biến ngẫu nhiên. Nên để đánh giá mức độ phân tán trung bình của giá trị biến ngẫu nhiên theo đơn vị đo của nó, người ta dùng một đặc trưng mới đó là độ lệch tiêu chuẩn.

Định nghĩa. Độ lệch tiêu chuẩn của biến ngẫu nhiên X bằng căn bậc hai phương sai của biến ngẫu nhiên X, ký hiệu

 VarX

Ví dụ 1.26.

Cho biến ngẫu nhiên liên tục X có hàm mật độ xác suất

fx

3 x2 3 x khi x 0;4



0

32 8

khi x 0;4

Kỳ vọng của biến ngẫu nhiên X :

EX xf xdxx 



4

3

3 



0



32 8

x 2 x dx



x3 x2 dx x 4 

4 

3

3



3

1

4



0 32 8



128 8

x3 

0

2

Phương sai của biến ngẫu nhiên X:

4

Ta tính E X x





2





2

f x dx x x2 x dx





2





3

3 

0

32 8



x 4 x3 dx x5 

4 

3

3



3

3

4



0 32 8



160 32

x 4 

0



24

5

Ta có VarX E X 2EX 2244 4

5

Độ lệch chuẩn của biến ngẫu nhiên X:

5

 

2 5

5

VarX

Giá trị tin chắc nhất của biến ngẫu nhiên X, ký hiệu ModX .

Trường hợp X là biến ngẫu nhiên rời rạc có bảng phân phối xác suất:

Thì Mod của biến ngẫu nhiên xác định là:

ModX xipiMax p1, p2,..., pn,...

1.6.3 Giá trị tin chắc nhất.

X

x1	x2	…	xn	…
P	p1	p2	…	pn	...

Có thể bạn quan tâm!

• Thống kê ứng dụng trong kinh tế và kinh doanh - Trường ĐH Văn Lang - 1
• Thống kê ứng dụng trong kinh tế và kinh doanh - Trường ĐH Văn Lang - 2
• Nếu X Là Biến Ngẫu Nhiên Rời Rạc Có Bảng Phân Phối Xác Suất Cho Bởi
• N I N N
• Biểuđồ Mứcchênhlệchgiữaphânphốichuẩnvà Student
• Tiêu Thức Bất Biến Và Tiêu Thức Biến Động.

Xem toàn bộ 142 trang tài liệu này.

Trường hợp X là biến ngẫu nhiên liên tục với hàm mật độ xác suất f xthì Mod xác định là:

ModX x0f0Maxf x , x 

Ý nghĩa. Giá trị tin chắc nhất của biến ngẫu nhiên là giá trị của biến ngẫu nhiên mà đại diện nhất cho phân bố. Về mặt hình vẽ ta có hai trường hợp như sau:

Trường hợp X là biến ngẫu nhiên rời rạc:

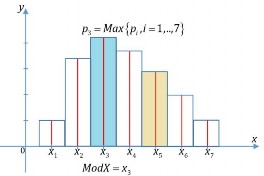
Hình 1.9: Mod biến ngẫu nhiên rời rạc

Trường hợp X là biến ngẫu nhiên liên tục:

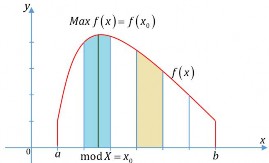
Hình 1.10: Mod biến ngẫu nhiên liên tục

Lưu ý. Giá trị tin chắc nhất có thể không duy nhất.

Ví dụ 1.27.

Tìm Mod của biến ngẫu nhiên rời rạc X có bảng phân phối xác suất

X

1	2	3	4	5
P	0,05	0,15	0,3	0,3	0,2

Dễ dàng nhận thấy, ModX 3 hoặc ModX 4

Ví dụ 1.28.

Cho biến ngẫu nhiên liên tục X có hàm mật độ:



3 x2 3 x khi x 0;4

f x 

0

32 8

khi x 0;4

Ta sẽ tìm giá trị lớn nhất của

f x khi x 0;4

Ta có

f 'x 3 x 3 , x 0;4. Xét

f 'x 0 ta thu được x 2 .

16 8

Giá trị

f 00 ;

f 40 ;

f 23

8



Vậy Max f x f 2. Vậy ModX 2

x 0;4

Trung vị của biến ngẫu nhiên X, ký hiệu MedX .

Trường hợp X là biến ngẫu nhiên rời rạc, có bảng phân phối xác suất

1.6.4 Trung vị

X

x1	x2	…	xn	…
P	p1	p2	…	pn	...

MedX xi khi mà:

P X x 1



i







P X x 

i

2

1

2

P X x 1

hay



i











2

P X x 



i



1

2

Trường hợp X là biến ngẫu nhiên liên tục, MedX m khi mà:

P X mP X m1

2

Ý nghĩa. Trung vị của biến ngẫu nhiên là giá trị của biến ngẫu nhiên chia phân phối xác suất của biến ngẫu nhiên thành hai phần bằng nhau.

Nếu ta xét trong trường hợp biến ngẫu nhiên liên tục, thì về mặt hình học, trung vị là giá trị của biến chia vùng diện tích của hàm mật độ xác suất làm hai phần có diện tích bằng nhau.

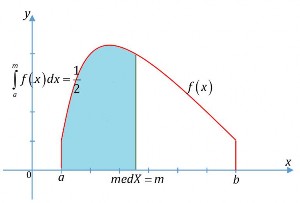
Hình 1.11: Trung vị biến ngẫn nhiên

Nhận xét. Trường hợp X là biến ngẫu nhiên rời rạc, có F x là hàm phân phối xác suất, thì ta có:

medX x

F x 1 F x 

i i2

i 1

Trường hợp X là biến ngẫu nhiên liên tục, có F x là hàm phân phối xác suất, thì ta có:

m1

Ví dụ 1.29.

medX m F mf x dx 

2



X	1	2	3	4
P	0.1	0.2	0.3	0.4

Giả sử biến ngẫu nhiên rời rạc X có bảng phân phối xác suất như sau:



P X 30,3 1P X 30,3 1



Ta có 2



P X 30,4 1

2

hay 2



P X 30,6 1

2

Theo định nghĩa ta có medX 3 .

4 2

4 2

Ví dụ 1.30.

Giả sử biến ngẫu nhiên liên tục X có hàm mật độ xác suất cho bởi

4x3 khi 0 x 1

f x 

Theo định nghĩa ta có med m nếu P X mP X mvới m0;1

0 khi x 0 x 1

1

2

fxdx 0,5 4x3dx 0,5 x 4

m m

m

0

0,5 m4 m 

1

1



Vậy trung vị medX 1

0

2

CHƯƠNG 2

Mục lục chương 2

2.1 Phân phối nhị thức 22

2.2 Phân phối siêu bội 26

2.3 Phân phối Poisson 30

2.4 Phân phối chuẩn 31

2.5 Phân phối Chi bình phương 35

2.6 Phân phối Student 37

Định nghĩa (Phép thử Bernoulli). Phép thử mà ta chỉ quan tâm đến biến cố A có xảy ra hay

không được gọi là phép thử Bernoulli.

2.1 Phân phối nhị thức

Ví dụ 2.1 Một sinh viên thi kết thúc môn học A, ta quan tâm kết quả sinh viên này thi có đạt hay

không đạt. Phép thử này là phép thử Bernoulli.

Định nghĩa (Biến ngẫu nhiên Bernoulli). Thực hiện một phép thử Bernoulli, ta quan tâm đến

biến cố A có xảy ra hay không. Đặt : X 0 nếu biến cố A không xảy ra.

1 nếu biến cố A xảy ra.

Giả sử P AP X 1p . Khi đó biến ngẫu nhiên X được gọi là biến ngẫu nhiên Bernoulli với tham số p, ký hiệu X ~ B p



Bảng phân phối xác suất của biến ngẫu nhiên Bernoulli có dạng

X

0 1
P	q = 1 − p p

Dựa vào bảng phân phối xác suất của biến ngẫu nhiên Bernoulli có EX p và VarX pq

Ví dụ 2.2 Sinh viên A trả lời một bài tập trắc nghiệm có bốn lựa chọn trong đó chỉ có một lựa chọn đúng, giả sử sinh viên này chọn câu trả lời một cách ngẫu nhiên. Ta đặt biến ngẫu nhiên



X 0

1

nếu sinh viên trả lời sai. nếu sinh viên trả lời đúng.

thìX ~ B p. Bảng phân phối xác suất của X

X	0	1
P	3/4	1/4

Trong thực tế ta thường thực hiện liên tiếp nhiều phép thử Bernoulli và đếm số lần xảy ra biến cố A trong các lần thực hiện đó. Phân phối xác suất số lần xảy ra A được trình bày ở mục kế tiếp.

Định nghĩa (Phân phối nhị thức).Thực hiện n phép thử Bernoulli độc lập với xác suất xảy ra

biến cố A trong mỗi phép thử là p. Đặt biến ngẫu nhiên

X 0 nếu biến cố A không xảy ra ở lần thử thứ i .

i



1 nếu biến cố A xảy ra ở lần thử th ứ i .

Biến ngẫu nhiên X X1X2... Xnchỉ số lần A xảy ra trong n lần thực hiện.

Biến ngẫu nhiên X được gọi là có phân phối nhị thức tham số n và p; ký hiệu X ~ B n, p

Ví dụ 2.3 Quan sát quyết định mua hàng của 5 khách hàng bước vào một cữa hàng quần áo. Dựa trên kinh nghiệm từ trước, quản lý cửa hàng ước lượng xác suất khách hàng sẽ mua hàng là 0,3 và biết các khách hàng mua hàng độc lập với nhau. Các vấn đề liên quan đến số lượng khách hàng mua hàng gồm:

a. Xác suất có 3 khách hàng sẽ mua hàng là bao nhiêu.

b. Trung bình sẽ có bao nhiêu khách hàng sẽ mua hàng.

c. Độ lệch trung bình xung quanh giá trị trung bình của khách hàng sẽ mua hàng là bao nhiêu.

d. Số khách hàng chắc chắn nhất sẽ mua hàng hàng là bao nhiêu.

Ví dụ 2.4 Một xạ thủ bắn 3 phát đạn vào một mục tiêu một cách độc lập, xác suất trúng mục tiêu

ở mỗi lần bắn là 0,7. Gọi các biến ngẫu nhiên:

X 0 nếu phát thứ i không trúng mục tie âu.

i



1 nếu phát thứ i trúng mục tiêu.

Vậy biến ngẫu nhiên : X X1 X2 X3 ~ B 3;0.7là số phát trúng mục tiêu trong 3 phát. Giá trị có thể của X là 0; 1; 2:

Ta thử tính xác suất có 2 phát trúng mục tiêu:

0.70.70.3 0.72 0.3 nếu viên 1,2 trúng.

P X 2 0.70.30.7 0.7 0.3 nếu viên 1,3 trúng. 30.7 0.3 C 0.7 0.3





2

2

2

3





2

0.30.70.7 0.72 0.3 nếu viên 2,3 trúng.

Định lý. Biến ngẫu nhiên X ~ B n, p

n

i. Xác suất có đúng k lần biến cố A xảy ra P X k Ck pk qnk

; k 0,...,n

ii. EX np

iii. VarX npq với q = 1- p

iv. np q ModX np q 1 , người ta còn gọi ModX là số lần xuất hiện tin chắc nhất.

Chứng minh.

Bởi vì X ~ B n, pcho nên : X X1 X2 ... Xn . Với Xi ~ B p. Kỳ vọng EX EX1 EX2 ... EXn np

Các biến ngẫu nhiên X1 , X2 ,..., Xn độc lập nên : VarX VarX1 VarX2 ... VarXn npq

Gọi P

P X k ; xét tỷ số

Pk P X k n k 1p1

Pk 1 P X k 1kq

k

suy ra Pk

là dãy không giảm khi và chỉ khi k np q 1

Tương tự

Pk Pk 1

1 là dãy không tăng khi và chỉ khi k np q

Từ hai điều trên ta thu được:

np q ModX np q 1

Ví dụ 2.5 Một bài thi trắc nghiệm có 10 câu hỏi, mỗi câu hỏi có bốn lựa chọn trong đó chỉ có một lựa chọn đúng. Một sinh viên trả lời ngẫu nhiên tất cả các câu. Gọi X là số câu trả lời đúng của sinh viên này.

a. Tính xác suất sinh viên trả lời đúng 2 câu.

b. Tính giá trị kỳ vọng, phương sai và Mod của biến ngẫu nhiên X.

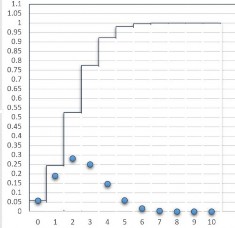
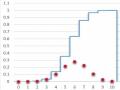
BNN	Mật độ	Phân phối
0	0.0563135	0.0563135
1	0.1877117	0.2440252
2	0.2815676	0.5255928
3	0.2502823	0.7758751
4	0.145998	0.9218731
5	0.0583992	0.9802723
6	0.016222	0.9964943
7	0.0030899	0.9995842
8	0.0003862	0.9999704
9	2.861E-05	0.999999
10	9.537E-07	1

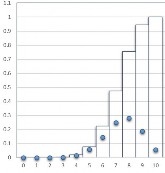
Hình 2.1: Đồ thị

f x và F x của X ~ B 10;0.25



1

Giải. Gọi biến ngẫu nhiên Xi 

nếu trả lời đúng câu i.

Trong đó

0 nếu trả lời sai câu i.

PXi10.25 ; i 1,...10 .Biến ngẫu nhiên số câu đúng

X X1 X2 ... X10 ~ B 10;0.25

a. Xác suất sinh viên trả lời đúng 2 câu :

10

PX2C20.252.0.7580.2816

b. Kỳ vọng của biến ngẫu nhiên X :

và phương sai :

EX np 10 0.25 2.5

VarX npq 100.250.75 1.875

số lần xuất hiện chắc nhất (ModX ) thỏa điều kiện :

np q ModX np q 1

thay số vào ta được :

vậy ModX 3

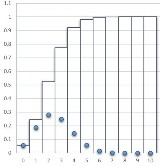
X ~ B 10;0.25

X ~ B 10;0.5

X ~ B 10;0.75

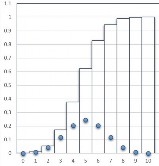
X ~ B 5;0.5

X ~ B 10;0.5

X ~ B 15;0.5

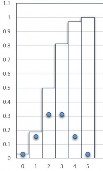
Hình 2.2: Đồ thị

f x và F x của X ~ B 10;0.25; B 10;0.5; B 10;0.75

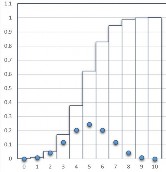
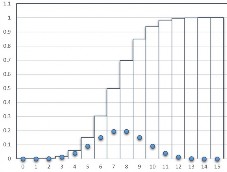
Hình 2.3: Đồ thị

f x và F x của X ~ B 5;0.5; B 10;0.5; B 15;0.5

Trong EXCEL, phân phối nhị thức được tính thông qua lệnh : BINOM.DIST

Number_s : số lần thành công

k 

Trials : số lần thực hiện phép thử n

Probability_s : xác suất 1 lần thành công p

Cumulative : bằng 0 nếu là hàm mật độ xác suất, bằng 1 nếu là hàm phân phối.

Ví dụ 2.6 Với X ~ B 10;0.5

P X 50.2461

Ví dụ 2.7 Có 9% sinh viên đại học nợ thẻ tín dụng lớn hơn 7000 USD (Reader Digest, tháng 7, 2002). Giả sử chọn ngẫu nhiên 10 sinh viên đại học để phỏng vấn về việc sử dụng thẻ tín dụng. Giả sử số sinh viên có mức dư nợ thẻ tín dụng cao hơn 7000 USD, X, là biến ngẫu nhiên có phân

.....

⇦ Trang trước - Trang tiếp theo ⇨