Nếu X Là Biến Ngẫu Nhiên Rời Rạc Có Bảng Phân Phối Xác Suất Cho Bởi

X .Y

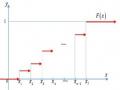
z1	z2	…	zk
P	P1	P2	…	Pk

Có thể bạn quan tâm!

Xem toàn bộ 142 trang tài liệu này.

Trong đó z1;z2;...; zkxi. y j/ i 1,n; j 1,m

Và Pl P X .Y zl 

Ví dụ 1.15.



xi ; y j : xi . y j zl

P X xi .P Y y j 



xi ; y j : xi . y j zl

piqj

Cho hai biến ngẫu nhiên rời rạc X ;Y độc lập có bảng phân phối xác suất lần lượt:

X	-1	1	2	3
P	0,3	0,4	0,2	0,1

Y	1	3	5
P	0,3	0,5	0,2

Ta có bảng phân phối xác suất của X Y dạng:

X Y

0	2	3	4	5	6	7	8
P	0,09	0,27	0,06	0,29	0,1	0,13	0,04	0,02

Trong đó:

P X Y 0P X 1.P Y 10,3.0,3 0,09

P X Y 2P X 1.P Y 3P X 1P Y 10,3.0,5 0, 4.0,3 0,27

P X Y 3P X 2.P Y 10,2.0,3 0,06

P X Y 4P X 1.P Y 5P X 1.P Y 3P X 3.P Y 1

0,3.0,2 0, 4.0,5 0,1.0,3 0,29

P X Y 5P X 2.P Y 30,2.0,5 0,1

P X Y 6P X 1.P Y 5P X 3.P Y 30,4.0,2 0,1.0,5 0,13

P X Y 7P X 2.P Y 50,2.0,2 0,04

P X Y 8P X 3.P Y 50,1.0,2 0,02

1.5 HÀM CỦA BIẾN NGẪU NHIÊN.

Cho biến ngẫu nhiên X và

f x là một hàm số xác định tại mọi giá trị trong tập giá trị của biến

ngẫu nhiên X , thì Y f X là một biến ngẫu nhiên mới và là hàm theo biến ngẫu nhiên X .

1.5.1 Hàm của biến ngẫu nhiên rời rạc.

Cho biến ngẫu nhiên X rời rạc có bảng phân phối xác suất

…

Và Y f X là hàm theo biến ngẫn nhiên X .

Bảng phân phối xác suất của biến ngẫu nhiên Y có dạng

…

Y f X 

Theo nguyên tắc:

Tập giá trị của biến ngẫu nhiên Y : y1, y2,..., ykf x1, f x2,..., f xn.

Giá trị xác suất : PiP Y yi

x j ; f x j yi

pj .

Ví dụ 1.16.

Cho biến ngẫu nhiên X rời rạc có bảng phân phối xác suất:

X		1	2	3	4
P		0,4	0,3	0,2	0,1
Bảng phân phối xác suất của biến ngẫu nhiên Y X 2 có dạng:
	Y X 2	1	4	9	16
	P	0,4	0,3	0,2	0,1
Ví dụ 1.17.
Cho biến ngẫu nhiên X rời rạc có bảng phân phối xác suất:
X		-1	1	2	3
P		0,4	0,3	0,2	0,1
Bảng phân phối xác suất của biến ngẫu nhiên Y X 2 có dạng

Y X 2

1	4	9
P	0,7	0,2	0,1

Trong đó P Y 1P X 21P X 1P X 10,4 0,3 0,7 . Cũng như P Y 4P X 24P X 2P X 20,2 0 0,2.

P Y 4P X 2 9P X 3P X 30,1 0 0,1 .

1.5.2 Hàm của biến ngẫu nhiên liên tục.

Cho biến ngẫu nhiên X rời rạc có hàm mật độ xác suất

nhiên X .

f x . Và Y hX là hàm theo biến ngẫn

Gọi G y là hàm phân phối xác suất của biến ngẫu nhiên Y , ta có:

G y P Y y P hX y 

f x dx

x ,hx y



Và gy là hàm mật độ xác suất của biến ngẫu nhiên, ta có:

gy G 'y 

Ví dụ 1.18.

Cho biến ngẫu nhiên liên tục X có hàm mật độ xác suất

4x3 khi 0 x 1

f x 

0 khi x 0 x 1

Và hàm biến ngẫu nhiên Y X 3, lập hàm mật độ xác suất cho biến ngẫu nhiên Y . GọiG y là hàm phân phối xác suất cho biến ngẫu nhiên Y .

3 y

G y P Y y P X y P X 













y f x dx









3 y

Nếu 0 y 0 ta có G y 0dx 0



Nếu 0 

1 0 y 1 ta có Gyfxdx4x3dxx4

3 y 3 y

y 3



Nếu 1 

1 y ta có G yfxdxfxdx0dx 1

3 y



0



; y 0

Vậy G y y







1



;0 y 1

;1 y



Ta có hàm mật độ của biến ngẫu nhiên Y X 3có dạng:

gy

0

;y 0;1

;y 0;1

3 y

43 y

3

1.6 CÁC ĐẶC TRƯNG CỦA BIẾN NGẪU NHIÊN.

1.6.1 Kỳ vọng

I. Kỳ vọng biến ngẫu nhiên rời rạc.

Định nghĩa. Giả sử biến ngẫu nhiên rời rạc X có bảng phân phối xác suất

…

...

Kỳ vọng của X , ký hiệu EX , là một số được định nghĩa:

EX xi pi

i 1



Ví dụ 1.19.

Gọi X là biến ngẫu nhiên chỉ số nút nhận được khi tung xúc sắc. Ta có bảng phân phối xác suất của X

1	2	3	4	5	6
1	1	1	1	1	1
6	6	6	6	6	6

X P

thì kỳ vọng của biến ngẫu nhiên X

EX 1121314 15161213,5

6 6

Nhận xét. Giá trị 3,5 cũng chính là số nút trung bình nhận được khi tung một xúc sắc.

Ví dụ 1.20.

Một người tham gia vào một trò chơi vòng xoay roulette, (Một bánh xe xoay xung quanh tâm, trên bánh xe có 38 ô tương ứng với các ô 00, 0, 1, 2, 3,…, 35, 36), tương ứng với ô 00 là màu trắng, ô 0 là màu xanh, các ô chẵn (2, 4,…, 36) màu đỏ, và các ô lẻ (1, 3,…, 35) màu đen. Có nhiều hình thức đặt cược trong trò chơi, và người này đặt cược vào chẵn lẻ. Giả sử người này đặt cược vào ô chẵn

$1, trung bình trong một lượt chơi thì người này thắng hay thua bao nhiêu tiền.

Gọi X là biến ngẫu nhiên chỉ số tiền người này được hay mất sau mỗi lượt chơi, thì X 1,1.

Tương ứng với giá trị xác suất là

P X 118và P X 120.

38 38

Nghĩa là người này tham gia trò chơi 38 lần thì có 18 lần người này được $1 và 20 lần người này mất $1. Trung bình số tiền về mặt tần số là

EX $1. 18 $1. 20 $0.053 38 38

Vậy trung bình một lượt chơi thì người này mất hơn 5 cent.

Nhận xét. Về mặt hình ảnh ta có thể quan sát như sau:

-0,053

Hình 1.6: Hình ảnh kỳ vọng

Coi 1 và 1 là hai cột mốc trên thanh đòn nằm ngang. Tại đây ta đặt hai quả cân có khối lượng

là 10 đơn vị tại 1 và 9

tại 1 . Thì giá trị EX 0,053 là cột mốc trên thanh đòn mà tại đó

19 19

thanh đòn cân bằng như hình vẽ.

Dựa trên hai ví dụ 3.4 và 3.5 ta đưa ra ý nghĩa của kỳ vọng của biến ngẫu nhiên:

Ý nghĩa. Tiến hành n phép thử, giả sử X là biến ngẫu nhiên nhận các giá trị có thể x1; x2;...; xkvới

số lần (tần số) n1;n2;...;nk. Giá trị trung bình của biến ngẫu nhiên X trong n phép thử là

X 

x n ... x n

1 1

k k

x ... x p n ...p n .

k 1 1 k k

p , i 1,...,k



là xác suất để biến ngẫu nhiên X nhận giá trị x . Nên theo công thức

kỳ vọng ta có về mặt giá trị trong tình huống này: X EX ; Kỳ vọng của biến ngẫu nhiên

chính là giá trị trung bình theo xác suất của biến ngẫu nhiên. Nó phản ánh giá trị trung tâm của phân phối xác suất.

Và hình ảnh để diễn tả cho kỳ vọng như sau: cho một thanh đòn không có khối lượng và trên đó đặt các khối tròn có khối lượng lần lượt là pi , i 1,..,k tại các điểm có tọa độ xitrên thanh đòn.

Ta có thể hình dung lúc này kỳ vọng của biến ngẫu nhiên chính là tọa độ của điểm trên thanh

đòn mà tại đó giúp thanh đòn thăng bằng.

…

pk 1

…

k 1

Hình 1.7: Hình ảnh kỳ vọng

II. Kỳ vọng biến ngẫu nhiên liên tục.

Định nghĩa. Giả sử biến ngẫu nhiên liên tục X có hàm mật độ xác suất là f x , kỳ vọng của biến ngẫu nhiên X được định nghĩa:

EX xf x dx





Ví dụ 1.21.

Biến ngẫu nhiên liên tục X có hàm mật độ :

Kỳ vọng của biến ngẫu nhiên X:

1;x 0;2

f x 2



0 ;x ;02;

2 1 2

EX xf x dx 2 xdx 1

0 0

III. Tính chất kỳ vọng biến ngẫu nhiên.

1. Tính chất kỳ vọng biến ngẫu nhiên.

X, Y là hai biến ngẫu nhiên bất kỳ và C thì kỳ vọng của biến ngẫu nhiên có các tính chất sau:

i. E C C

ii. E CX C EX 

iii. E X Y EX EY

iv. Nếu hai biến ngẫu nhiên X và Y độc lập thì E XY EX .EY

2. Tính chất kỳ vọng hàm biến ngẫu nhiên.

Cho biến ngẫu nhiên X có hàm mật độ xác suất f x , kỳ vọng của hàm của biến ngẫu nhiên hX 

có thể được xác định bằng cách

Đặt Y hX , xác định hàm mật độ xác suất gy của Y và tính kỳ vọng của biến ngẫu nhiên Y



E hX EY ygy dy



Tuy nhiên, để tính kỳ vọng E hX không cần thiết phải tìm hàm mật độ của biến ngẫu nhiên

hX mà ta có thể tính E hX trực tiếp bằng tính chất sau:

i. Nếu X là biến ngẫu nhiên rời rạc có bảng phân phối xác suất cho bởi

Kỳ vọng của biến ngẫu nhiên hX là:

E hX hxipi

i 1

ii. Nếu X là biến ngẫu nhiên liên tục có hàm mật độ xác suất f x thì kỳ vọng của biến



Tính chất kỳ vọng hàm biến ngẫu nhiên. Cho h là hàm số thực bất kỳ

x1	x2	…	xn	…
P	p1	p2	…	pn	...

ngẫu nhiên hX là:



E hX hx f x dx



Ví dụ 1.22.

Cho biến ngẫu nhiên rời rạc X có bảng phân phối xác suất:

-1	1	2	3
P	0,1	0,2	0,4	0,3

Để đối chiếu kết quả kỳ vọng của biến ngẫu nhiên X 2 , ta có 2 cách tính như sau

Cách 1. Lập bảng phân phối xác suất cho biến ngẫu nhiên X 2

Y X 2

1	4	9
P	0,3	0,4	0,3

Kỳ vọng của biến ngẫu nhiên Y X 2 là

EY E X 2 10,3 40,4 90,3 4,6

Cách 2. Sử dụng công thức tính kỳ vọng hàm biến ngẫu nhiên: E X 2120,1 120,2 220,4 320,3 4,6 Hai cách tính đều cho kết quả E X 24,6 .

Ví dụ 1.23.

Cho biến ngẫu nhiên liên tục X có hàm mật độ xác suất

4x3 khi 0 x 1

f x 

0 khi x 0 x 1

Kỳ vọng của biến ngẫu nhiên Y X 3, kết quả tính và đối chiếu thông qua 2 cách:

Cách 1. Lập hàm mật độ xác suất cho biến ngẫu nhiên Y X 3

Theo ví dụ 2.11) ta có hàm mật độ của biến ngẫu nhiên Y có dạng:

gy 

0

;y 0;1

;y 0;1

Vậy theo định nghĩa kỳ vọng biến ngẫu nhiên Y bằng:

EY ygy dy y.

1



3 ydy y 3 dy .

4 1 4

4 3

3 0

3 7

7 1



Cách 2. Sử dụng công thức kỳ vọng cho hàm biến ngẫu nhiê liên tục ta có:

E X 3x3f x dx x3.4x3dx 4.





0

Đối chiếu hai kết quả ta có kỳ vọng của biến ngẫu nhiên Y X 3bằng 4.

43 y

3

1.6.2 Phương sai

I. Định nghĩa phương sai biến ngẫu nhiên.

Đặc trưng thứ nhất của biến ngẫu nhiên là kỳ vọng, thể hiện giá trị trung tâm của biến ngẫu nhiên.

Đăc trưng thứ hai thể hiện mức phân tán trung bình của các giá trị của biến ngẫu nhiên có thể

nhận được xung quanh giá trị kỳ vọng.

Giả sử ta có biến ngẫu nhiên X rời rạc, nhận các giá trị

xi với i 1,2,...,k . Như vậy biến ngẫu

x2 EX 0

x1 EX 0

X k 1 EX 0

Xk 1

x3 EX 0

X k EX 0

nhiên thể hiện mức chênh lệch của giá trị biến ngẫu nhiên so với kỳ vọng là Y X EX . Và biến ngẫu nhiên Y có thể nhận các giá trị âm và dương như hình vẽ dưới.

Hình 1.8: Giá trị biến ngẫu nhiên phân bố xung quanh kỳ vọng

Trong một số trường hợp EY 0 và điều này không phản ánh đúng mức phân tán của giá trị biến ngẫu nhiên xung quanh kỳ vọng.

Để khắc phục điều này, ta không tính trực tiếp sai lệch của giá trị biến ngẫu nhiên so với kỳ vọng, mà ta tính thông qua trị tuyệt đối hoặc bình phương sai lệch. Và để thuận tiện trong việc tính toán thì ta tìm trung bình của bình phương các sai lệch.

Định nghĩa. Cho biến ngẫu nhiên X có kỳ vọng là EX . Phương sai của X, ký hiệu là VarX , được định nghĩa:

VarX E XEX 2

Áp dụng các tính chất của kỳ vọng ta có công thức tính phương sai:

VarX E X EX 2E X 2EX 2

Trường hợp X là biến ngẫu nhiên rời rạc.



VarX E X2EX 2x2px p 

Trường hợp X là biến ngẫu nhiên liên tục.



i i

i 1



i 1



i i 



2

VarX E X 2EX 2x 2f x dx xf x dx 



Ví dụ 1.24.

Một chủ vườn thanh long thu hoạch trên hai thửa ruộng, mỗi thửa 10 quả bất kỳ, thu được bảng trọng lượng (gram) của từng quả như sau:

Thửa 1

380	420	380	420	380	400	420	400	420	380
Thửa 2	400	500	300	300	500	300	400	450	450	400

Gọi X1, X2là biến ngẫu nhiên chỉ trọng lượng một quả thanh long trên thửa 1; 2.

a. Tính kỳ vọng của X1 , X2 .

b. Tính phương sai của X1 , X2 .

Kỳ vọng của biến ngẫu nhiên X1 , X2 lần lượt bằng:

EX 380. 4 400. 2 420. 4 400

EX 300. 3 400. 3 450. 2 500. 2 400

a. Ta có bảng phân phối xác suất của X1 , X2 là

380

400

420

300

400

450

500

Nhận xét. Kỳ vọng về trọng lượng của một quả thanh long trồng trên hai thửa là bằng nshau. Nếu bạn là người thu mua thanh long, bạn sẽ chọn của thửa nào?

b. Phương sai của biến ngẫu nhiên X1 :

1 1 1

VarX

EX 2EX 2

4 2 4 

4 2 4 2

3802. 4002. 4202. 380. 400. 420. 320

10 10 10 10 10 10 

Phương sai của biến ngẫu nhiên X2 :

VarX

EX 2EX 23002.3

4002. 3 4502. 2 5002. 2 

2 2 2 

10 10 10 10 



3 3 2 2 2



300.10 400. 10 450. 10 500.10 

5500

Nhận xét. Nếu theo định nghĩa phương sai, là kỳ vọng của bình phương sai lệch của biến ngẫu nhiên so với giá trị kỳ vọng biến ngẫu nhiên, vậy trong ví dụ này với kỳ vọng của 2 biến ngẫu nhiên là bằng nhau, thì phương sai về trọng lượng của quả thanh long của thửa ruộng hai lớn hơn của thửa 1 nghĩa là các quả thanh long của thửa 1 “đều” hơn so với thửa 2. Và nếu chọn thu mua, thì thanh long của thửa 1 sẽ được ưu tiên chọn hơn.

Ví dụ 1.25.

Biến ngẫu nhiên liên tục X có hàm mật độ xác suất

f x 

4x3

0

khi 0 x 1

khi x 0 x 1

Phương sai của biến ngẫu nhiên X là:



VarX E X EX x













f x dx xf x dx













2





1

2

x2.4x3dx x.4x3dx 4x5dx 4x 4dx 

1

2

0

0

0



II. Tính chất phương sai.

Cho hai biến ngẫu nhiên X, Y và hằng số thực C , phương sai có các tính chất sau

Xem tất cả 142 trang.

Ngày đăng: 06/11/2023