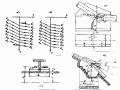
pháp đồ giải không những xác định được trị số áp lực nước va lớn nhất mà còn có thể vẽ được sơ đồ áp lực nước va ở bất cứ tiết diện nào trên đường ống đơn lẫn ống phức tạp.
n
Nhờ khả năng đa năng của nó nên phương pháp đồ giải được sử dụng phổ biến. Sau đây trình bày nội dung tính toán của phương này. Để tính toán đồ giải ta vẫn sử dụng các hệ phương trình nước va mắc xích tương đối (14-13) và (14-14), vẫn sử dụng
điều kiện ban đầu turbine phản kích.
B 0 , cần xây dựng lại điều kiện biên tại A-A cho phù hợp với
1. Chọn toạ độ trường và biểu diễn các nhóm phương trình mắc xích
Căn cứ vào nhóm phương trình truyền sóng nghịch (14-13) và thuận (14-14):
A B
2( v A v B )
(14-13)
n(n1)
B A
n(n 1)
n
n
2( v B
(n1)
v
A
(n 1))
(14-14)
biểu thị quan hệ giữa
và v , do vậy ta chọn hệ trục toạ độ trường như hình (14-9):
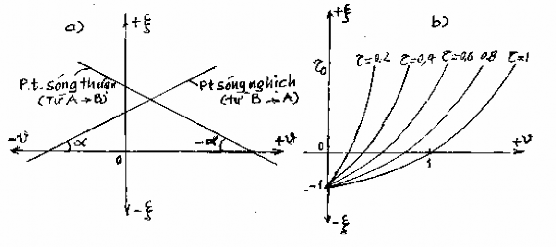
Hình 14-9. Biểu diễn phương trình mắc xích trên hệ trục ~ v.
Nhận thấy mỗi nhóm phương trình đều là đường thẳng đi qua hai điểm có toạ
độ A ( v A ,A ) và B( v B ,B) . Nhóm phương trình sóng nghịch (14-13) là đường thẳng
làm với trục hoành một góc (có tg = 2); nhóm phương trình sóng thuận (14-14) là đường thẳng làm với trục hoành một góc có tg = - 2. Do vậy khi giải, nếu biết một điểm trên đường có thể dựa vào điều kiện ban đầu hay biên nữa là có thể xác định được
điểm kia. Trước hết ta cần biểu diễn điều kiên biên tại A-A là độ mở tương đối
f ( v,) trên hệ toạ đô, trong đó a(tbin phản kích) hay F(tb. gáo)
amax
2. Biểu diễn các đường đồng độ mở f ( v,) trên hệ trục
1
a. Đường đồng độ mở vẽ cho turbine xung kích:
Fmax
Theo điều kiện biên tại A: công thức (14-15):
v
. Để vẽ các đường
đồng f ( v,) , ta định trước các giá trị = 0 - 0,2 - 0,4 - 0,6 - 0,8 -1. Mỗi độ mở
ta giả thiết các giá trị
với
và dùng công thức (14-15) tính ra tương ứng các v. Như vậy
mỗi độ mở ta vẽ được một đường f ( v,) (hình 14-9,b). Chú ý rằng các đường
đều đi qua điểm có toạ độ (0, -1) vì với các nhưng khi = -1 thì v = 0. Còn với = 1 khi v = 1 thì = 0 nên đường = 1 đi qua điểm có toạ độ (1, 0).
b. Đường đồng độ mở vẽ cho turbine phản kích:
Để vẽ các đường đồng độ mở f ( v,) cho turbine phản kích ta sử dụng
1
1
đường đặc tính tông hợp chính của turbine. Đổi trục qua lập bảng 14-1 sau đây:
n' sang trục và trục
Q' sang v
Bảng 14-1. Tính toán để vẽ các đường đồng f ( v,)
1 | . . . | 0,2 | |||||||
a amax | . . . | n' 10 | . . . | . . . | n' 10 | . . . | . . . | n' 10 | . . . |
n' 1 | |||||||||
⎛n' ⎞2 ⎜10⎟1 ⎝n' ⎠ 1 | |||||||||
Q' 1 | Q' 10 | Q' 10 | Q' 10 | ||||||
Q' v 11 Q' 10 |
Có thể bạn quan tâm!
-
Phân Loại Và Lắp Đặt Đường Ống Bêtông Cốt Thép -
Phương Trình Cơ Bản Của Nước Va Trong Ống Đàn Hồi -
Vẽ Biểu Đồ Áp Lực Nước Va Dọc Theo Tuyến Ống -
Một Số Quy Định Về Trị Số Giới Hạn Max Trong Tính Bảo Đảm Đc Tổ Máy -
Tuabin thủy lực - 29 -
Trường Hợp Không Xét Tới Sức Cản Thuỷ Lực
Xem toàn bộ 317 trang tài liệu này.
1
Tính chuyển đổi từ
n' sang
: từ công thức
' n D1 1
n D1
H
(1 ) H0
=
(*); khi
n
10
chưa có nước va thì '
n D1
n
(**) . Khai triển (*) và (**) để hai vế của chúng đều
H0
2 ⎛n' ⎞2
1
bằng (n D1) , cân bằng hai công thức và rút ra công thức chuyển đổi: ⎜
10⎟1;
Tính chuyển
đổi từ
⎝n' ⎠
(1 )H0
1
Q' sang v: Từ công thức quy dẫn của turbine
H
1 1
Q D
=
1 1
Q Q' D 2 ' 2
; lưu lượng lớn nhất nhưng chưa có nước va
Qmax
Q' D 2
H0
. Lập tỷ số v
Q Q'
1
Q
, rút ra công thức chuyển: v 1
10 1
Qmax '
10
⎛' ⎞2 Q'
1
Từ hai công thức chuyển đổi ⎜n10⎟1 và v 1
ta tiến hành tính
1
Q
10
⎝n' ⎠'
toán bảng (14-1) như sau theo các bước sau:
- Dòng 1: định các độ mở tương đối: = 1 - 0,8 - 0,6 - 0,4 - 0,2 - ...
- Có độ mở cánh hướng dòng lớn nhất a max
độ mở a theo công thức ghi trong bảng (dòng 2);
trên đường đặc tính turbine, tính ra
1
- Định các trị số
n' (dòng 3) và tra được các
Q' tương ứng (hình 14-10,a), ghi
1
vào dòng 5; tính ra các
6).
tương ứng (ghi vào dòng 4); tương ứng tính ra các v (dòng
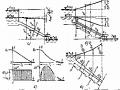
Hình 14-10. Tra đường đặc tính tổng hợp chính của turbine.
Từ kết quả tính ở bảng (14-1) các cặp v, ứng với từng độ mở a. Vẽ được các
đường đồng độ mở f ( v,) trên hệ trục đối với turbine phản kích (hình 14-10,b).
3. Đồ giải đối với ống đơn giản
a. Đồ giải trường hợp giảm tải
Trước tiên ta lấy trường hợp giảm tải từ đầy tải đến đóng toàn bộ turbine để xét (từ 0 1 đến c 0)
Hình 14-11. Đồ giải khi từ đầy tải đến đóng toàn bộ.
- Trước tiên định ra quy luật đóng turbine f (t) , từ quy luật này tiến hành vẽ các đường đồng độ mở f ( v,) với các 0 1 , 2t , 4t , 6t 0 như hình (14-11).
- Tính tg =
~ v (hình 14-11).
2và vẽ tam giác cân có hai góc lên bên cạnh hệ trục toạ độ
- Dựa vào điều kiện biên và ban đầu để xác định các điểm: tại thời điểm
t i ở A
sẽ có toạ độ điểm
Ai ( vi , i ) , tại B cũng có toạ độ điểm
Bi ( vi , i ) , như vậy từng thời
điểm ta biết được trị số áp lực nước va tương đối
i ứng với
vi . Xác định các điều
kiện biên, điều kiện ban đầu trước khi đồ giải. Tại đầu thời đoạn t = 0, lúc này chưa xảy
ra nước va nên
v A v B 1 vậy hai điểm
A 0 (1 , 0 ) B0 (1 , 0 ) , sau nửa pha t = l/c
0 0
sóng truyền từ A đến B và vì cuối thời điểm t= l/c nước va mới tới gần B nên vận tốc tại
B chưa đổi nên
v B v A 1 . Do vậy ba điểm
A 0 (1 , 0 ) B0 (1 , 0 )
Bt (1 ,0 ) . Vậy ta
t 0
xác định được ba điểm trên hệ trục ~ v. Áp dụng các phương trình truyền sóng mắc xích (14-13) và (14-14) cùng với các điều kiện biên cụ thể để giải như sau:
2t
+ Để xác định áp lực nước va cuối pha thứ nhất tại A ( A ) tức là tìm điểm
2t 2t
A 2t ( v A ,A ) ta viết phương trình truyền sóng thuận từ A đến B sau:
B A 2( v B v A ) .
t 2t t 2t
Phương trình này là đường thẳng đi qua điểm
Bt ( vB,B) đã biết và làm với trục hoành
t t
2t 2t
một góc và điểm A 2t ( v A ,A ) cần tìm. Điểm A 2t lại thuộc điều kiện biên tại A là
2t . Vậy điểm A 2t
là giao diểm của đường thẳng đi qua Bt ( vB,B) và đường 2t .
t t
3t 3t
+ Xác định điểm B3t ( v B ,B) , viết phương trình sóng nghịch từ B đến A:
A B 2( v A v B )
Điểm
2t 3t 2t 3t
B3t nằm trên đường thẳng đi qua điểm
A 2t và làm với trục hoành một góc và
nằm trên trục hoành (vì
B 0 ). Vậy từ
A 2t kẻ đường thẳng trên và cắt trục hoành ta
được điểm B3t cần xác định.
+ Cũng bằng cách này ta tiếp tục xác định được các điểm A 4t , B5t , A 6t , B7t , ... Nếu không kể tổn thất thì các điểm cứ giao động , tuy nhiên do có tổn thất nên chúng sẽ tắt dần quanh gốc toạ độ. Nối các điểm A tại ta được đường biểu diễn áp lực nước va dương tại mặt cắt A-A.
Nhận xét chung:
* Từ biểu đồ ta thấy Sau khi đóng kín turbine trong ống có phát sinh nước va âm, có khả năng sinh chân không làm bẹp đường ống.
* Phương pháp đồ giải còn có khả năng xác định áp lực nước va tại một mặt cắt bất kỳ của đường ống. Ta hãy lấy ví dụ xác định áp lực nước va ở mặt cắt D-D nằm ở giữa đường ống. Vì D-D ở giữa ống nên thời gian truyền sóng từ A đến D và từ D đến B đều là 0,5t. Ta tiến hành đồ giải đê xác định áp lực nước va tại D như sau:
Đầu thời đoạn ta cũng có điểm
D0 (1 ,0 ) ; thời điểm 0,5t cũng có
D0,5t (1 ,0 ) .
Vậy các điểm
D0 D0,5t Bt A 0 B0 ta đặt chúng lên hệ trục (hình 14-11). Tiến
hành đồ giải như sau:
+ Tìm điểm A t , nó là giao điểm của của phương trình sau:
D A 2( v D v A )
0,5t t 0,5t t
và điều kiện biên t . Từ D0,5t kẻ đường thằng này (nét đứt) gặp t được
+ Tìm điểm D1,5t , nó là giao điểm của hai đường :
A t .
A D 2( v A v D )
t 1,5t t 1,5t
B D 2( v B v D
) , được điểm D1,5t
A t
t 1,5t t 1,5t
+ Tìm điểm B2t , nó là giao điểm của dường:
D B 2( v D v B ) và trục hoành.
1,5t 2t 1,5t 2t
+ Tìm điểm D 2,5t , nó là giao điểm của hai đường sau:
A D2( v A v D )
2t 2,5t 2t 2,5t
B D 2( v B v D )
2t 2,5t 2t 2,5t
+ Tìm điểm A3t , nó là giao điểm của đường:
D A 2( v D v A ) và điều kiện biên 3t .
2,5t 3t 2,5t 3t
+ Tiếp tục như trên ta tìm được các điểm D3,5t , B4t , D 4,5t , A5t , ... Nối các
điểm D lại với nhau (đường nét đứt) ta được đường biểu diễn áp lực nước va dương tại mặt cắt D-D. Tìm các điểm ở trên theo trình tự truyền sóng nước va sau:
D0 D0,5t At D1,5t B2t D2,5t A 3t D3,5t
...
* Chú ý ở trên ta vừa xét cách đồ giải cho trường hợp đóng từ đầy tải đến đóng toàn bộ, từ đó suy ra các trường hợp đóng sua đây:
- Đóng từ đầy tải ( 0 1 ) đến độ mở cuối nào đó ( c 0 ) (hình 14-12,a) ;
- Đóng từ chưa đầy tải ( 0 1 ) đến đóng hoàn toàn ( c 0 ) (hình 14-12,b);
- Đóng từ chưa đầy tải ( 0 1 ) đến độ mở nào đó ( c 0 ) (hình 14-12,c) .
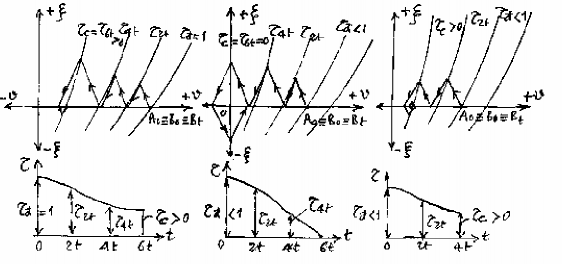
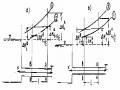
Hình 14-12. Một số trường hợp đồ giải và cách đồ giải.
Việc tiến hành đồ giải đối với mặt cắt A-A cũng tương tự chỉ có khác là chọn
điều kiện ban đầu từ và điều kiện biên thích hợp với từng trường hợp.
b. Đồ giải trường hợp tăng tải
Tiến hành đồ giải trường hợp tăng tải cũng tién hành tương tự, chỉ khác là thao tác từ trái sang phải và bên dưới trục hoành. Sau đây trình bày cách đồ giải cho trường hợp tăng tải từ độ mở ban đầu ( 0 0 ) đến độ mở cuối ( c 1 ) , quy luật mở tương đối như hình vẽ (14-13). Dựa vào quy luật mở f (t) ta vẽ các diều kiện biên tại A-A
như hình vẽ. Vẽ tam giác cân có góc . Xác định các điểm theo điều kiện ban đầu tại
A và B ta có
A 0 ( v A , 0 ) B0( v B , 0 ) Bt ( vB,0) vì v A v B v B .
0 0 t 0 0 t
Hình 14-13. Đồ giải trường hợp tăng tải.
2t 2t
+ Tìm áp lực nước va cuối pha thứ nhất, điểm A 2t ( v A , A ) là giao điểm của: phương trình : B A 2( v B v A ) và 2t . Ta xác định được A 2t .
t 2t t 2t
3t 3t
+ Tìm điểm B3t ( v B , B ) , nó là giao điểm của phương trình đường:
A B 2( v A v B ) và trục hoành (vì B 0) .
2t 3t 2t 3t
+ Và cứ tiếp tục cách như vậy ta sẽ lần lượt xác định các điểm
A 4t , B5t , A 6t ...
giao động xung quanh có toạ độ ( vc , 0 ) . Nối các điểm A lại ta có đường biểu diễn trị
số áp lực nước va âm tương đối tại điểm mặt cắt A-A.
Nhận xét: Qua đồ thị ta thấy trường hợp tăng tải sóng nước va yếu dần. Hình thức yếu dần này theo hai khả năng: + Mang tính chu kỳ lúc (-) lúc (+) (xem hình vẽ);
+ Tắt dần không chu kỳ (không sinh nước va (+)
4. Đồ giải đối với ống có đặc tính thay đổi dọc ống
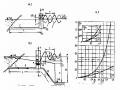
Lấy ví dụ dồ giải cho đường ống (hình 14-14,a) có hai đoạn DB và DA, tương
ứng có kích thước như hình vẽ và các thông số
v DB
, v DA
, cDB, cDA , đoạn
max max
DB có DB nên có tg2DB , còn đoạn DA có tg2DA tương ứng ta vẽ hai tam giác ngược với các góc cho đoạn BD và góc cho đoạn DA xem
hình vẽ (14-14,b). Quy luật đóng f (t) cho ở hình (14-14,a). Thời gian truyền sóng
t AD 0,2s, thời gian truyền sóng t DB 0,4 s , thời gian đóng hết turbine Ts 1,6 s .
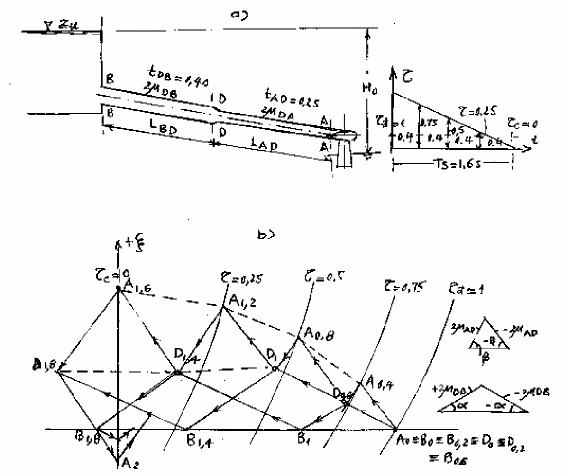
Hình 14-14. Đồ giải áp lực nước va ống có đặc tính thay đổi dọc ống.
Xác định các điều kiện ban đầu là: tại B-B luôn có
B 0 nên các điểm B đều
nằm trên trục hoành. Các điểm
A 0 B0 D0 D0,2 B0,2 B0,6 và có toạ độ (1, 0).
Điều kiện biên tại A-A là f ( v , ) đã vẽ trên hình (14-14,a). Tiến hành đồ giải:
+ Tìm điểm
A 0,4 ( v A
, A
) , nó là giao điểm của phương trình đường thẳng:
0,4 0,4
D A
2DA ( v D
v A
) và biên 0,4 0,75
điểm A 0,4
0,2 0,4 0,2 0,4
+ Tìm điểm D0,6 ( v D , D ) , nó là giao điẻm của hai đường thẳng sau:
0,6 0,6
A D 2DA ( v A v D )
0,4 0,6 0,4 0,6
B D 2DB ( v B v D ) được điểm D0,6 .
0,2 0,6 0,2 0,6
1 1
+ Tìm điểm B1( v B, B) , nó là giao điểm của trục hoành và đường thẳng;
D B 2DB ( v D v B)
được điểm B1 .
0,6 1 0,6 1
+ Tìm điểm A0,8 ( v A , A ) nó là giao điểm của phương trình đường thẳng:
0,8 0,8
D A 2DA ( v D v A ) và biên 0,8 0,5 được điểm A0,8 .
0,6 0,8 0,6 0,8
1 1
+ Tìm điểm D1( v D, D) , nó là giao điểm của hai phương trình đường thẳng:
B D 2DB ( v B v D)
0,6 1 0,6 1
A D 2DA ( v A v D)
được điểm D1 .
0,8 1 0,8 1
+ Tìm điểm A1,2( v A , A ) , nó là giao điểm của phương trình đường thẳng:
1,2 1,2
D A 2AD ( v D v A )
và 1,2 0,25
được điểm A1,2 .
1 1,2 1 1,2
+ Tìm điểm D1,4 ( v D , D ) , nó là giao điểm giữa hai đường thẳng:
1,4 1,4
B D 2DB ( v B v D )
1 1,4 1 1,4
A D 2DA ( v A v D
) được điểm D1,4 .
1,2 1,4 1,2 1,4
+ Tìm điểm A1,6 ( v A , A ) , nó là giao điểm giũa phương trình:
1,6 1,6
D A 2DA ( v D v A ) và biên c 0 được điểm A1,6 .
1,4 1,6 1,4 1,6
+ Và cứ thế ta lần lượt xác định các điểm tiếp theo. Nối các điểm A ta được đường biểu diễn áp lực nước va tại A-A, nối các điểm D lại ta có đường biểu biễn áp lực nước va tại D-D.
Chú ý: Khi viết phương trình truyền sóng giữa A và D phải thời đoạn là 0,2 s, khi viết phương trình truyền sóng giữa B và D phải lấy thời đoạn là 0,4 s.
5. Đồ giải đối với ống phân nhánh
Ta xét ống phân nhánh (hình 14-15,a) gồm hai nhánh AD' và CD''', với trường hợp mặt cắt C đóng từ đầu và trong suốt quá trình không mở, đầu ống A đóng mở theo
quy luật ác = f(t) (hình vẽ) và dựa vào quy luật này vẽ được điều kiện biên tại A là các
. Các điều kiện khác gồm có: B 0 , vC 0 , tại D luôn có điều kiện :
q D'' q D' q D'''
v D'' v D ' v D '''
Lập ba hệ toạ độ
~ v ~
cho riêng ba đoạn ống : AD', CD''', D''B với các
thông số
AD' ,
CD''' ,
D'' B
và các góc
tương ứng (xem hìmh 14-15,b). Sau đó
tiến hành đồ giải như sau:
Trên đoạn AD': Trước khi đóng (mở) thì điểm
A 0 ( v A , A ) trùng với điểm D'
0 0
1 1
1
ở thời đoạn 1 s là D'1( v D ' , D ' ) tại v = 1, nghĩa là: A0 D0D'(1, 0) .
2 2
+ Sau 2 s (tức 1 pha) ta có điểm A 2( v A , A ) là giao của phương trình đường:
1 2
1 2
D' A 2
AD '
( vD' v A )
và điều kiện biên 2 , được điểm A 2 .
3 3
+ Tìm điểm D'3( v D ' , D ' ) sau thời gian 3s , nó nằm trên đường đi qua A 2 :
2 3
2 3
A D'
2AD '
( v A v D')
và một đường nữa chưa biết, cần phải phải xét thêm đoạn ống khác nữa để xác định.
Trên đoạn CD''': Ở trạng thái ban đầu (tức là sau 2sec) khi ở A thay đổi thì ở C
2
2
chưa thay đổi, nên C 0 còn vC 0 (vì van C đóng) vậy điểm C 2( 0 , 0 ) .