Trường Hợp Không Xét Tới Sức Cản Thuỷ Lực

trường hợp đó với hệ số nhám lấy nhỏ nhất, phụ tải giảm đột ngột từ lưu lượng lớn nhất

đến lưu lượng bằng không;

- Khi tính mực nước thấp nhất trong BĐA lấy mực nước hồ là mực nước chết, tổn thất thuỷ lực trong đường dẫn là lớn nhất có thể xảy ra với hệ số nhám lớn nhất với các trường hợp tăng tải sau:

+ Tăng công suất tương ứng với một tổ máy, nhưng không nhỏ hơn 33% công suất toàn nhà máy đối với nhà máy có công suất nhỏ hơn 30 MW;

+ Tăng công suất tương ứng với hai tổ máy, nhưng không nhỏ hơn 50% công suất toàn nhà máy đối với nhà máy có công suất lớn hơn 30 MW;

+ Tăng từ công suất nhất định đến toàn bộ công súât nhà máy, hoặc với một giá trị công suất mà nhà máy tham gia điều chỉnh tần số của mạng điện.

Mực nước thấp nhất trong BĐA, để tránh không khí lọt vào turbine tối thiểu phải lấy cao hơn mép trên của ống dẫn turbine từ 2 đến 3m.

Đối với BĐA hạ lưu sau ống xả thì mọi điều kiện công suất, tổn thất phải chọn ngược lại với tính toán trên của BĐA thượng lưu.

XV. 4. 1. Tính toán thuỷ lực BĐA hình trụ

1. Trường hợp không xét tới sức cản thuỷ lực

Có thể bạn quan tâm!

Xem toàn bộ 317 trang tài liệu này.

Ta xét một hệ thống dẫn nước áp lực lý tưởng của TTĐ là làm việc không có tổn thất thuỷ lực và thay đổi lưu lượng tức thời. Với điều kiện đã nêu, ta bỏ qua tổn thất htt trong (15-2) và giảm công suất đến không (QT = 0) trong (15-3), ta có hai phương trình:

dV gZ

(15-2') và

dZ fV

(15-3');

dt L dt F

Đạo hàm phương trình (15-3') theo thời gian t và cân bằng với (15-2') ta nhận được:

d 2 Z 

dt 2

fg Z 0 LF

(15-4)

Giải phương trình (15-4), giao động Z có dạng (hình 15-9,a):

Z = Z0 sin (kt + ) (15-5)

Trong đó: Z0 là giao động cực đại mực nước trong BĐA so với mực nước tĩnh

của hồ; k =

là tần số giao động;  là pha đầu.

Điều kiện ban đầu khi t = 0, Z = 0 và  = 0 thì:

Z = Z0 sin kt (15-6)

Giao động mực mực nước trong BĐA khi không có tổn thất cột nước là giao động điều hoà không tắt (hình 15-9,a), có chu kỳ :

T 2 2 k

(15-7)

Để tìm độ giao động mực nước cực đại trong BĐA, ta đạo hàm (15-6) theo t:

dZ  Z dt0

k.cos kt;

sau đó lấy bình phương biểu thức vừa nhận được và (15-6), rồi cộng chúng lại, ta có:

1 ⎛dZ ⎞2

⎜⎟ Z2  Z2

(*)

k 2 ⎝ dt ⎠0

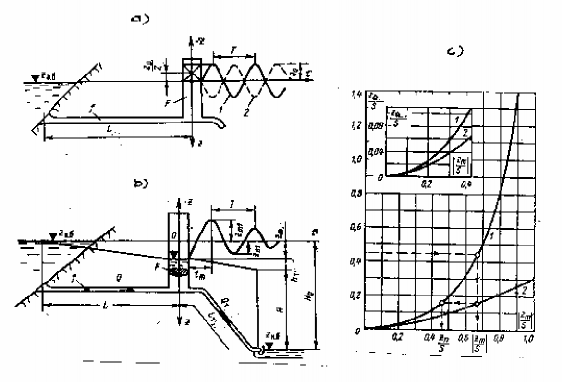
Hình 15-9. Giao động mực nước trong BĐA

a) Giao động mực nước khi không xét tổn thất thuỷ lực: 1, 2- khi giảm hoặc tăng lưu lượng tức thời;

b) Giao động mực nước khi cắt toàn bộ phụ tải có kể đến tổn thất thuỷ lực;

c) Biểu đồ để xác định mực dâng và giảm cực đại troamtron BĐA hình trụ khi đóng tức thời, toàn bộ turbine: 1- xác định mực nước Zm; 2- xác định Zn.

Biết rằng khi t = 0, Z = 0 và

dZ  f V

, thay vào (*) ta rút ra được:

Z0 V0

dt F 0

(15-8)

Nếu lưu lượng turbine giảm tức thời từ lưu lương ban đầu (QT0 ) xuống lưu lượng cuối (QTc) tương ứng với vận tốc trong đường dẫn V0 và Vc thì mực nước dâng cực đại trong buồng điều áp sẽ là:

Z0  (Vc

 V0 )

(15-9)

Các công thức (15-8) và (15-9) dùng được cho cả trường hợp tăng tải khi xác

định mực nước giảm trong BĐA hình trụ.

2. Trường hợp xét tới sức cản thuỷ lực

a . Xét trường hợp ngắt tải: giả thiết rằng lưu lượng trong ống turbine thay đổi tức thời từ lưu lượng ban đầu (QT0) xuống lưu lượng cuối (QTc). Ở chế độ ổn định trước khi ngắt tải mực nước trong BĐA thấp hơn mực nước trong hồ một đoạn Zđ (hình 15-

9,b) bằng tổng tổn thất cột nước dọc đường dẫn, cột nước cục bộ và tổn thất cột nước vận tốc tại nơi tiếp nối giữa đường dẫn và BĐA, được biểu thị theo công thức:

L V 2 V 2

Z  h

 (

 1)00

(15-10)

0 tt.0

d cb 2g 2g

Và trong chế độ dòng không ổn định ta có tổn thất:

V 2

h tt 2g

(15-11)

Cần thấy rằng khi giảm tải hoàn toàn QT = 0 thì từ (15-3) ta có:

F dZ

dV F d 2

F2 ⎛dZ ⎞2

V 

và Z. Khi đó: h tt ⎜⎟

f dt

dt f

dt 2

2gf 2 ⎝dt ⎠

Đặt htt và dV/dt vào (15-2) ta nhận được phương trình giao động mực nước trong BĐA khi có tính đến sức cản thuỷ lực, như sau:

d 2 F

⎛dZ ⎞2 fg

Z⎜⎟

Z  0

(15-3')

dt 2 2fL ⎝ dt ⎠ LF

Ta ký hiệu các hằng số trong (15-3'):

k1 

F 2gL

và k 2

 fg LF

rồi giải phương

trình sẽ được nghiệm chung của phương trình (15-3') khi cắt toàn bộ phụ tải:

⎛dZ ⎞2

k ⎛ 1 ⎞

2k Z 2

⎜⎟ C1e 1 ⎜⎜ Z ⎟⎟

(15-12)

⎝ dt ⎠

k1 ⎝

2k1 ⎠

Dựa vào điều kiện ban đầu: khi t = 0 thì Z = h0

⎛dZ ⎞

và

⎜dt ⎟

, rồi thay C1

vào (15-2), có:

k ⎛dZ ⎞21

⎝⎠t0

1⎜⎟ h 

e2k1( h0Z) 

k 2 ⎝ dt ⎠0 2k

(15-12')

k ⎛dZ ⎞21

1⎜⎟ Z 

k 2 ⎝ dt ⎠ 2k1

Mực nước dâng cực đại trong BĐA hình trụ Zm có thể được xác định từ (15-12')

V 2 k ⎛dZ ⎞2

khi dZ/dt = 0. Biết rằng h

.01⎜⎟, ta nhận được biểu thức Zm :

tt.0

2g k 2 ⎝dt ⎠

e2k1(h0Zm) 

2k1

1  Z

2k1

(15-12'')

Đặt số hạng ở mẫu số

2k1

 Lf

F

 S , lấy lôgarit phương trình (15-12'') ta nhận

được các trị số không thứ nguyên để xác định Zm :

Zm 

ln⎛

Zm ⎞Z0

(15-13)

⎜1

⎟

S ⎝ S ⎠ S

Dựa vào phương trình (15-13) để xác định biên độ giao động mực nước cao nhất trong BĐA. Mực nước cao nhất của buồng được tính với mực nước hồ là MNDBT.

Để tiện tính toán có thể xây dựng đồ thị quan hệ

Zm ~ Z0

S S

(xem hình 15-9,c) để

tìm giao động cực đại mực nước trong BĐA khi tức thời giảm lưu lượng lưu lượng của turbine từ ( QT.0) nào đó đến lưu lượng cuối QTC = 0. Dùng đường 1 để tìm Zm, còn đường 2 để tìm giao động mực nước hạ Zn trong BĐA.

Trong thực tế tính thấy rằng sức cản thuỷ lực trong hệ thống dẫn có ảnh hưởng rất lớn đến biên độ giao động mực nước trong BĐA, ví dụ với đường dẫn dài L = 1 km thì biên độ này có sai khác 13% , và khi L = 20 km sai khác tới 25% so với trường hợp không kể sức cản . Tác giả I.A. Trernhichin đưa ra công thức tính gần đúng khi có kể dến sức cản thuỷ lực như sau:

Zm = Z0(1-0,681. + 0,154.2) (15-14)

Trong đó: Z0 tính khi không kể đến sức cản (theo phương trình 15-9);

h tt.0

; khi  = 0÷2 thì sai số dới 2,3% so với tính chính xác.

b- Xét trường hợp tăng tải: Tăng tải với lưu lượng turbine từ lưu lượng ban đầu QT.0 lên lưu lượng cuối QT.C với trạng thái ổn định. Tính toán coi như mở tức thời, công thức xác định mực nước hạ thấp nhất trong BĐA sẽ là:

Zn Z0

(1 n){1 0,156 1  2n (1 n) . [1  (1 n)]} n2Z

2 n0

(15-15)

Với: n QT .0

QTC

, còn htt.c

Z 0

( trong đó htt.c là tổn thất thuỷ lực cuối thời đoạn)

Nếu tăng lưu lượng turbine tức thời từ đầu bằng không QT0 = 0 đến QT.C thì:

Zn [1 0,078(1 )]Z0

(15-16)

Chú ý: các công thức (15-14), (15-15) và (15-16) chỉ phù hợp khi  < 1,24, còn khi

 > 1,24 thì giao động không có chu kỳ và mực nước hạ thấp nhất bằng tổn thất cột nước cuối thời đoạn Zn = htt.c.

XV. 4. 2. Tính toán thuỷ lực BĐA có kết cấu cản

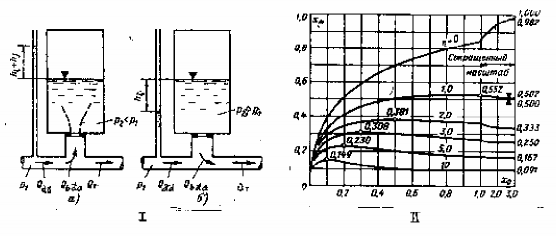
Hình 15-10. Nguyên tắc làm việc ở nút cản

I- Sơ đồ nguyên tắc làm việc của nút cản: a) khi giảm tải; ) khi tăng tải II- Biểu đồ xác định mực nước cực đại khi đột ngột cắt toàn bộ phụ tải.

Khi có mặt cản phụ (ví dụ màng cản) đặt ở nơi tiếp nối giữa BĐA hình trụ và đường dẫn áp lực sẽ làm thay đổi đáng kể chế độ thuỷ lực của hệ thống dẫn nước có áp. Ở chế độ ổn định thì cản phụ không làm việc, lúc này mực nước trong BĐA thấp hơn mực nước thượng lưu một trị số bằng tổn thất cột nước ban đầu, theo công thức (15-10):

V 2 L

V 2 V 2

Z0 htt.0 hL hcb 0 (cb  1)00

2g d 2g 2g

Ở chế độ không ổn định do tác dụng của kết cấu cản nên: Khi giảm tải (hình 15- 10,a) áp suất phía sau vật cản (tức ở thân trụ) p2 nhỏ hơn áp suất p1 phía trước vật cản, do vậy cản có tác dụng tiêu hao bớt năng lượng của dòng chảy qua nó và làm tắt giao động nhanh hơn khi không có cản phụ. Sự chênh lệch áp suất này còn làm cho áp lực nước va lan sang đường dẫn. Ngược lại khi tăng tải (hình 15-10, ) thì p2 > p1 cản trở việc hạ thấp mực nước trong buồng. Đặc trưng cho nút cản là hệ số kháng thuỷ lực 

V 2

qua nút cản. Tổn thất cột nước qua nút cản là

h.bda

biết Vbda = Qbda / f (trong đó:

f - tiết diện đường dẫn; Qbda, Vbda- tương ứng là lưu lượng và vận tốc dòng nước trong BĐA).

a- Xét trường hợp cắt tải: Từ điều kiện cắt tải ( QTC = 0) và áp dụng công thức (15-2) và (15-3') cho trường hợp có nút cản ta có:

dV 

g Ltd

(Z htt

h)

(15-17)

dZ f V dt F

(15-18)

Trong công thức (15-17) tổng tổn thất cột nước trong đường dẫn và chỗ vào

V 2

BĐA sẽ bao gồm:

h htt h

hL hcb 2g h

(*)

Biểu diễn tỷ lệ tổn thất cột nước ở cản phụ theo tổn thất htt (là tổn thất chưa kể

đến cản phụ) thì:

h.0 h



Z0 htt

L  1 

d cb

Ký hiệu y = V/V0 và xem là: Vbda = V viết lại (*) ta có: h = (1 + ) Z0 y2 (**) Sử dụng (15-17), (15-18) và (**):

Z  (1 ) y 2

LfV 2

2gFZ0

d ( y 2 )

(15-19)

Đặt

LfV 2

S 0 

2gFZ0

F (L 

d cb

Lf

 1) F

(15-12')

chuyển thành các đại lượng không thứ nguyên: x = Z/S và x0 = Z0/S, rồi lấy tích phân phương trình vi phân (15-19), ta có kết quả cuối cùng ở dạng:

y (1 )x 1(1 )x0  1 e(1)( x0 x)

(15-20)

(1 )2 x (1 )2 x

Dựa vào (15-20) để tìm mực nước cao nhất trong BĐA. Khi mực nước trong BĐA đạt cao nhất (Zm) thì vận tốc trong đường dẫn V = 0 và y = 0 và đặt xm = Zm/S. Giải phương trình ta được:

ln  [1  (1 )xm]  (1 )xm ln[1  (1 )x0]  (1 )x0

(15-21)

Theo (15-21) ngời ta xây dựng họ đường cong xm = f( x0, ) (hình 15-10,II), dùng các đường này để xác định mực nước cao nhất trong BĐA có cản khi cắt tải. Dựa vào (15-12') tính ra S, biết Z0 và  tính được x0. Từ đó tra ra xm rồi tính ra Zm. Trên biểu đồ, đường ứng với  = 0 ứng với BĐA trụ thông thờng không có vật cản.

b- Xét trường hợp tăng tải: Mực nước thấp nhất trong BĐA xảy ra trong hợp tăng tải. Trong thiết kế chọn trường hợp tính toán là tăng toàn bộ 1 tổ máy từ lưu lượng không tải (Qx) đến đầy tải (Qmax) của một tổ máy hoặc tăng toàn bộ c tổ máy trong phạm vi điều chỉnh bình thường, ví dụ tăng từ 50% đến 100% phụ tải với mực nước thượng lưu thấp nhất. Việc tính toán bằng phương pháp giải tích trường hợp này rất phức tạp, do vậy nên dùng phương pháp đồ giải hoặc sử dụng các phương pháp số trên máy tính để giải sẽ tiện lợi hơn.

XV. 4. 2. Tính toán thuỷ lực BĐA hai buồng

Buồng điều áp hai buồng thường được sử dụng khi hệ thống áp lực dài, cột nước lớn, mực nước thượng lưu thay đổi nhiều và đá núi đặc chắt, hồ chứa có độ sâu tháo lớn.

a- Khi cắt toàn bộ phụ tải:

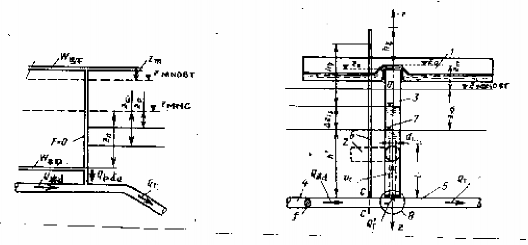
Thông thường giếng đứng nối hai buồng có tiết diện bằng tiết diện đường dẫn, bởi vậy mực nước dâng khi cắt tải sẽ nhanh chóng đạt đến đáy buồng trên hoặc đỉnh tràn. Với điều kiện này cho phép không tính đến thời gian dâng mực nước, mực nước nhanh chóng đạt cao nhất Zm trong buồng, thể tích nước vào buồng trên WBT có thể coi như xảy ra khi mực nước trong buồng là Zm (hình 15-11). Xác định công thức tính WBT

Hình 15-11.Sơ đồ tính BĐA hai buồng.

1- buồng trên; 2- buồng dưới; 3- giếng đứng; 4- đường dẫn; 5- ống turbine; 6- ống đo áp;

7- mực nước động trước khi thay đổi phụ tải; 8- nút cản; 9- Z0 mực nước cao nhất trong BĐA .

như sau: Giả sử có vật cản ở đáy giếng đứng (hệ số cản thuỷ lực của nút cản ). Ta sử dụng phương trình (15-17) và phương trình nữa để lập công thức tính:

dV 

g Ltd

(Z htt

h)

(15-17)

dW 

fVdt

(15-22)

phương trình (15-22) xác định thể tích phân tố nước qua đường dẫn sau thời gian dt khi lưu lượng turbine bằng không (QT = 0) và lượng nước thừa hoàn toàn vào BĐA. Tổn thất cột nước trong đường dẫn ở chế độ ổn định (*) và không ổn định (**) là:

V 2

Z 0 (L / d cb  1)0

V 2

(*)

htt h (L / d cb  1 ) 2g

(**)

Đặt y = V/ V0 và chia (**) cho (*) ta có:

htt hZ0

L / d cb  1

L / d cb  1

. Thay vào công thức (15-17), (15-22) ta có:

Z L / d  1

2 LfV d ( y )

2 2

cby Z0 L / d cb  1

2gZ 0dW

(15-23)

LfV 2d ( y 2 )

L / d  1

Đặt:

A 0

2gZ0dW

và B cb

L / d cb  1

, công thức (15-23) thành:

Z By 2

d ( y 2 )



(15-23')

Giải (15-23') để tìm thể tích nước trong buồng trên. Cận tích phân ứng với trước khi ngắt tải là: y = V/V0 = 1 và khi ngắt tải hoàn toàn là y = V/V0 = 0 cho kết quả :

LfV 2 B

WBT 0ln(1  )

2gZ0 B vm

(15-24)

Trong công thức (15-24) : vm Zm / Z0

Để xác định thể tích buồng trên cần phải biế giá trị Zm. Để làm điều này cần định ra một số giá trị Zm (thường theo điều kiện kinh tế lấy từ 812 m) và tính toán so sánh các trị số để chọn kết quả cuối cùng. Cũng cần chú ý rằng (15-24) được thành lập cho trường hợp đường kính giếng đứng nhỏ, và cũng vì giếng nhỏ nên dù có bố trí vật cản hay không thì tổn thất ở chỗ tiếp giáp với đường dẫn vẫn không thể bỏ qua.

b- Khi tăng tải:

n xnm)

xn m)

Tương tự trường hợp giảm tải, khi tăng tải đột ngột thì buồng dưới có tác dụng bổ sung nước cho ống turbine, do vậy mực nước trong BĐA đang ở vị trí ban đầu ổn định Z0 (tương ứng với lưu lượng turbine đầu QT.0) hạ xuống đến mực nước thấp nhất Zn (tương ứng lưu lượng turbine cuối QT.C) và được giữ ở mực nước này cho tới khi lưu lượng đường dẫn đạt giá trị QT.C. Thể tích cần thiết của buồng dưới được xác định :

LfV 2 x  1 (

xn  1)(

WBD cln

(15-25)

2gZc x m (

xn  1)(

Trong (15-25):

x Zn và m QT .0 ; Z là mực nước ổn định ứng với Q và

c QT .C

T .C

VC là vận tốc trong đường dẫn ở trạng thái ổn định sau khi tăng tải.

Cũng cần thấy rằng để xác định thể tích buồng dưới cũng cần định trước một số trị số Zn và chọn trên cơ sở so sánh kinh tế - kỹ thuật các phương án.

Trên đây trình bày phương pháp tính toán thuỷ lực xác địng kích thước buồng điều áp theo phương pháp giải tích đối với một số BĐA thường gặp, các trường hợp còn lại sinh viên có thể tìm hiểu ở các tài liệu Thuỷ lực và Thuỷ điện khác.

XV. 5. TÍNH TOÁN THUỶ LỰC BĐA BẰNG ĐỒ GIẢI

Đối với BĐA có hình dạng phức tạp, việc dùng phương pháp giải tích gặp nhiều khó khăn trong việc giải các phương trình, người ta sử dụng phương pháp đồ giải sẽ đơn giản hơn và kết quả nhận được cũng dễ nhận thấy hơn. Cơ sở lý luận của phương đồ giải cũng vẫn từ hai phương trình động lượng (15-2) và liên tục (15-3) được sai phân

hoá các thành phần vi phân thành sai phân:

dZ Z dt t

và dV

V

t

Từ phương trình (15-2) và (15-3) ta có:

V gt (Z h )

(15-26)

L tt

Z QT fV t

(15-27)

Mức độ chính xác của đồ giải tuỳ thuộc vào việc lựa chọn khoảng thời gian t, thường lấy theo chu kỳ T (công thức 15-7), với mức chính xác cho phép có thể lấy theo

như sau:

t = ( 1/321/40) T. Để đồ giải cần xác định sơ bộ kích thước BĐA theo điều

kiện ổn định sóng vô cùng bế trong đó. Sau đây trình bày cách đồ giải các loại BĐA.

1. Đồ giải đối với BĐA hình trụ

Để đồ giải cho BĐA hình trụ ta cần lập hệ toạ độ và biểu diễn các phương trình trên lên hệ trục. Ta biến đổi các phương trình (15-26) và (15-27) cụ thể như sau:

Phương trình (15-26) và (15-27) có thể viết lại như sau:

V (Z htt )

(15-28)

Z QT

gt

t 

f Vt F

(15-29)

L

V 2 2 2

Trong đó: đặt 

, và tổn thất

htt  ( d

cb  1) 2g 2g V

V ;