Vẽ Biểu Đồ Áp Lực Nước Va Dọc Theo Tuyến Ống

* Xét trường hợp sóng nghịch từ B đến A (hình 14-5,a):

Hình 14-5. Sơ đồ thành lập phương trình dây chuyền sóng nước va.

Mặt cắt A-A nằm về phía turbine, mặt cắt B-B nằm về phía hồ, cách nhau một đoạn l. Áp lực nước va đầu thời đoạn là đường (1) cao hơn áp lực nước va cuối thời đoạn - đường (2) vì đây là trường hợp sóng nghịch, trị số áp lực nước va giảm đi. Đầu

thời đoạn vận tốc và trị số áp lực nước va tại A-A là

VA , HA , tại B-B có V B, HB .

t t t t

Có thể bạn quan tâm!

• Tuabin thủy lực - 23
• Phân Loại Và Lắp Đặt Đường Ống Bêtông Cốt Thép
• Phương Trình Cơ Bản Của Nước Va Trong Ống Đàn Hồi
• Chọn Toạ Độ Trường Và Biểu Diễn Các Nhóm Phương Trình Mắc Xích
• Một Số Quy Định Về Trị Số Giới Hạn Max Trong Tính Bảo Đảm Đc Tổ Máy
• Tuabin thủy lực - 29

Xem toàn bộ 317 trang tài liệu này.

t l / c

Cuối thời đoạn vận tốc và áp lực nước va tại A-A là V A

A

, H

t l / c

, tại B-B là sẽ là:

V

B

t l / c

B

, H

t l / c

. Như vậy tại mỗi mặt cắt có sự thay đổi trị số áp lực nước va như sau:

Tại A-A: HA

HA c ( V A VA

) (*)

t l/ c

t g t

t l/ c

Tại B-B:

HB

HB c ( VB VB

) (**)

t l/ c

t g t

t l/ c

Trong hai công thức trên đầu vế phải có dấu trừ ví đây là sóng nghịch. Nếu bỏ

qua tổn thất ma sát thì nước va truyền đi không bị biến dạng nên:

HB HA và

t t l/ c

VB VA

. Biến đổi và cộng hai công thức (*) và (**) với nhau và sắp lại ta có:

t t l/ c

HA HB c ( VA V B )

(14-9)

t t l/ c g t

t l / c

Phương trình (14-9) là phương trình truyền sóng nghịch từ B-B về A-A.

*. Xét trường hợp sóng thuận từ A đến B (hình 14-5,b):

Hình (14-5,b) là sơ đồ để xác định phương trình dây chuyền sóng nước va thuận. Trên sơ đồ này đường (1) nằm thấp hơn dường (2) vì đây là sóng thuận tăng áp. Các ký hiệu và diễn giải để thành lập công thức tương tự trường hợp sóng nghịch, chỉ khác ngược chiều. Cũng có sự thay đổi áp lực nước va tại mỗi mặt cắt A và B như sau:

Tại A-A:

HA HA 

c ( V A V A

) (*')

t l / c t

g t t l / c

Tại B-B: HB HB c ( VB VB

) (**')

t l/ c t gt

t l/ c

Trong hai công thức trên đầu vế phải có dấu cộng ví đây là sóng thuận. Cũng bỏ

qua tổn thất ma sát thì nước va truyền đi không bị biến dạng nên:

HA HB và

t t l/ c

VA VB

. Biến đổi và cộng hai công thức (*') và (**') với nhau và sắp lại ta có

t t l/ c

phương trình truyền sóng thuận (14-10) từ A-A về B-B như sau:

HB HA

( V B V A

) (14-10)

c

t t l / c

g t t l / c

b. Phương trình sóng nước va gián tiếp, trị số tương đối

Để tiện tính toán người ta đưa trị số nước va tuyệt đối (14-9) và (14-10) về trị số nước va tương đối (không thứ nguyên) bằng cách sau đây:

Đặt H

H0

gọi là trị số áp lực nước va tương đối; H0 cột nước tỉnh chưaứinh nước va;

V Q

v q

là vận tốc và lưu lượng tương đối;

V max

c Qmax

2g H0 F

Qmax

c V max

2g H0

là hệ số quán tính đường ống.

Chia hai vế của các phương trình (14-9) và (14-10) cho

H0 và vế phải nhân với

tỷ số

V max , cuối cùng theo cách đặt các đại lượng không thứ nguyên trên ta có phương

V max

trình truyền sóng nước va gián tiếp trị số tương đối cho hai trường hợp sóng trên sau:

- Phương trình truyền sóng nghịch từ B về A:

A B 2( v A v B )

(14-11)

t t l / c t t l / c

- Phương trình truyền sóng thuận từ A về B:

B A 2( v B v A )

(14-12)

t t l / c t t l / c

Áp dụng tổng quát cho quá trình truyền sóng dây chuyền trên đường ống, ký

hiệu nửa pha nước va là 

= l/c. Vậy ta có hệ phương trình truyền sóng dây chuyền

nước va gián tiếp, sau đây viết cho t = n bất kỳ ( với n = 0, 1, 2, .., ...):

n

n

v

B

Truyền sóng nghịch: A

B



(n1)

2( v A

(n1))

(14-13)

Truyền sóng thuận :

B A





n(n 1)

2( v B

(n 1))

(14-14)

n

v

A

Các phương trình (14-13) và (14-14) gọi là phương trình truyền sóng, hoặc phương trình mắc xích vì dựa vào đó ch ta có thể xác được trị số áp lực nước va ở các nửa pha kế tiếp nhau khi biết các điều kiện biên và điều kiện ban đầu.

XIV. 2. 2. Tính toán nước va bằng phương pháp giải tích

Có thể dùng phương trình truyền sóng nước va tuyệt đối hoặc tương đối kết hợp với các điều kiện biên hoặc điều kiện ban đầu để tính áp lực nước va. Ở đây trình bày cách sử dụng các hệ phương trình truyền sóng tương đối (14-13) và (14-14) để tính với hai phương pháp: giải tích và đồ giải. Tiết này ta dùng phương pháp giải tích để giải.

1. Điều kiện biên và điều kiện ban đầu

Để giải bài toán nước va bằng phương pháp giải tích trước hết ta xác định các

điều kiện biên và điều kiện ban đầu ở hai mặt cắt A-A và B-B của đường ống.

n

- Tại mặt cắt B-B , nơi tiếp xúc với bể áp lực hoặc hồ chứa có kích thước lớn tại đây giao động mặt nước gần như không đổi do vậy coi như không có áp lực nước va nghĩa là: B 0 ;

- Tại mặt cắt A-A ở trước turbine: muốn tìm chính xác điều kiện biên tại đây cần nghiên cứu chế độ đóng mở cơ cấu hướng dòng hay van kim theo thời gian:

2gHA

* Đối với turbine xung kích, quy luật đóng mở theo quan hệ

QA 

, vậy vận tốc tương đối tại A-A ở cuối pha thứ nhất sẽ là:

QA 22g( H0 HA )

1 A

2

1 A

1

v

A 22Q max

2

2g H0

max 2

1

Và tương tự ta có điều kiện biên ở A-A ở cuối pha thứ n bất kỳ sẽ là:

QA

1 A

2n 

1 A

n

v A 2n

2n

n

, hay:

2n Qmax

n

v A n

(14-15)

1 A

n

n

Trong đó: v A

- vận tốc tương đối tại A-A ở cuối pha thứ n;

n

A - áp lực nước va tương đối tại A-A ở cuối pha thứ n.

n - độ mở tương đối của van kim cuối pha thứ n.

* Đối với turbine phản kích: quy luật đóng mở ở cuối pha n sẽ là:

1 2n

H0 HA

QA Q' D2

H0

v

A

2n

2n

Qmax

12n

Q

D

' 2

1 max 1

, lưu lượng qua turbine trong quá trình

chuyển tiếp rất phức tạp, phải dựa vào đường đặc tính của turbine để xác định các lưu

lượng dẫn xuất

Q'tương ứng với các độ mở CCHD ao

ứng với các cột nước cụ thể

1

(hay

n' cụ thể). Để giải bằng giải tích một cách rất gần đúng, nhà khoa học người Ý

1

Lêvi đưa ra giả thiết rằng: sự thay đổi lưu lượng quy dẫn

Q' tỷ lệ với độ mở cánh

1

Q' a 0 2n

hướng dòng ao , nghĩa là:12n2nn

(*); trong đó n là độ mở tương

Q

'

max

a 0 max

đối cơ cấu hướng dòng ở cuối pha thứ n. Vậy công thức (*) có thể ở dạng sau đây của

1 A

n

điều kiện biên tại A-A cuối pha thứ n trở về công thức (14-15) ở trên:

n n

v A 

(14-15)

- Điều kiện ban đầu: tại thời điểm t = 0 chưa xảy ra nước va, do vậy các đặc trưng H, Q tại các tiết diện óng đều ở chế độ ổn định, nếu bỏ qua tổn thất thuỷ lực thì

đường đo áp nằm ngang, có nghĩa là H = 0 nên

A B và

v A v B . Mặt khác khi

0 0

0 0

t

sóng truyền đến sát B-B với thời gian rất gần t = L/c thì coi như do vậy có thể coi như v A v B v B .

vB chưa kịp thay đổi,

0 0 t

2. Phương pháp giải tích cho đường ống đơn giản

Đường ống đơn giản là đường ống có đường kính, bề dày và vật liệu làm ống không đổi suốt chiều dài đường ống và không rẽ nhánh. Ta dùng các hệ phương trình mắc xích (14-3) và (14-4) và các điều kiện ban đầu và điều kiện biên (14-15) để giải lần lượt xác định áp lực nước va tương đối tại mặt cắt A-A cuối đường ống ở cuối các pha:

2

1 A ,

2 A ,

3 A , ...,

A





n 2n

khi biết chế độ đóng mở cửa van kim

4

6

(t) hoặc độ mở cánh hướng dòng a 0 (t) (hình 14-6).

Hình 14-6. Chế độ đóng mở tương đối cánh hướng nước.

2

a. Xác định áp lực nước va tương đối cuối pha thứ nhất (n = 1) 1 A :

Viết phương trình truyền sóng thuận từ A đến B (phương trình 14-3):

BA2( vBv A)

(*)



22

Dựa vào điều kiện biên tại B-B ta có

B 0

và điều kiện biên tại A-A ta có

v A 2

; dưạ điều kiện ban đầu tại B ta có

v B v A 0

0 ,

1 A

2

1 A

2

20

1 A

0

2

vậy thay chúng vào (*) ta có: A

2( 0

2

) và dùng ký hiệu theo cuối

pha rút ra phương trình xác định nghiệm áp lực nước va tương đối cuối pha thứ nhất:

1 1



1 0

1

2

(14-16)

4

b. Xác định áp lực nước va tương đối cuối pha thứ n

3

4

- Tìm áp lực nước va cuối pha thứ hai (n = 2)

2 A : ta viết phương trình

sóng thuận từ A đến B ta có:

B A

1 A

4





v

3

34

2( v B

v A

) , dựa điều kiện biên tại B

và A ta có:

B 0 và

A 4

. Cần tìm thêm

B viết phương trình

3

v

4

truyền sóng ngược từ B đến A ta có:

A B

1 A

2





3



23

2( v A

v B

) . Với

B 0 và

2

3

3

2

điều kiện biên tại A có: v A

2

, thay vào và rút ra v B

ta có nghiệm:

1 2





2 1

(14-17)

2 0 2

- Một cách tương tựa tién hành xác định nghiệm cho các pha thừ 3, 4, ... Ta có

2n

công thức nghiệm tổng quát cho cuối pha thứ n ( n A

) bất kỳ:

1 n

n 1n 1

n0 2

i i1

(14-18)

c. Nước va pha thứ nhất và pha giới hạn

Trong tính toán và lắp đặt đường ống áp lực vấn đề người ta quan tâm là xác

định được trị số áp lực nước va dương lớn nhất để tính toán độ bền đường ống và trị số

áp lực nước va âm nhỏ nhất để kiểm tra vị trí đặt ống tránh xuất hiện chân không trong

ống.Vì vậy ở đây chúng ta xem xét vấn đề thiết thực này.

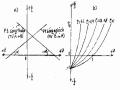
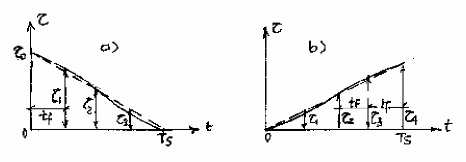
Qua thực tế tính toán và vận hành đường ống áp lực của TTĐ người ta thấy áp lực nước va lớn nhất max rơi vào một trong hai trường hợp: rơi vào cuối pha thứ nhất, tức là max 1 (hình 14-7,a) hoặc rơi vào pha cuối cùng, gọi là pha giới hạn, tức

max m

(hình 14-7,b). Sau đây chúng ta đi xác định các trị số nước va hai pha này.

Nước va pha thứ nhất max 1

Khi đóng mở van hay cánh hướng dòng, áp lực nước va đạt trị số lớn nhất ngay cuối pha thứ nhất, các pha tiếp theo có trị số nhỏ hơn. Do vậy ta chỉ cần tính toán trị số nước va cuối pha này. Từ phương trình nghiệm cuối pha thứ nhất (14-16) bình phương 2

vế và giải ra ta có nghiệm: 

2⎡( 02) 

⎤(*)

( 02) 2( 22)

1

0 1

1 ⎢⎣1 ⎥⎦

Cần chọn dấu của nghiệm của (*). Nếu chọn nghiệm có dấu (+) trong (*) thì nếu

đóng turbine từ độ mở tương đối ban đầu

0 1 (đầy tải) đến đóng toàn bộ ( 1 0 ) thì

22c Vmax Hmax 

điều này vô lý. Do vậy nghiệm sẽ là:

1 0 g H0 H0

( 02) 2( 22)

1

0 1

2⎡( 0 2) 

max

⎤(14-19)

1 ⎢⎣1 ⎥⎦

Nước va pha thứ nhất thường xảy ra ở TTĐ có cột nước cao (thường H  150 - 250 m).

Hình 14-7. Sơ đồ nước va pha thứ nhất và pha giới hạn.

Nước va pha giới hạn max m

Trong quá trình đóng mở turbine , áp lực nước va tăng dần và đạt gía trị lớn nhất

vào pha cuối

max (hình 14-7,b), tức là

max m , gọi là nước va pha giới hạn. Để

thành lập công thức tính áp lực nước va pha giới hạn ta dùng nghiệm (14-18) viết cho pha thứ (m -1) và pha m như sau:

1 m1

m1

1m2

m1

0 

2

i i1

(*)

1 m

m 1m1

m 0 

2

i i1

(**)

Từ hình (14-7,b) ta thấy có thể coi

m1 m

và lấy hai vế tương ứng của (*) và (**)

trừ cho nhau ta có:

( m m1)

1 

1 m

m

. Coi quá trình đóng mở theo quy

luật tuyến tính thì độ chênh độ mở tương đối



m1

m 

t f 

1 m

Ts

2 L

c Ts

từ đây suy

ra 

1 m m = 

m (***).

Ở đây .

2L c Qmax LV max là hệ số đặc trưng quán tính đường

c Ts 2gF H0 g H0 Ts

ống. Giải phương trình (***) ta được áp lực nước va giới hạn:

( 

m 2

2 4 )

(14-20)

Trong công thức trên, dấu (+) tương ứng với đóng, dấu (-) tương ứng với mở turbine. Nước va pha giới hạn thường xảy ra ở TTĐ có cột nuớc thấp.

Phán đoán pha nước va

1 

Để xác định áp lực nước va lớn nhất ta dùng hai công thức (14-19) và (14-20) tính ra, sau đó lấy trị số lớn hơn trong hai công thức. Tuy nhiên để giảm khối lượng tính toán ta có thể thành lập công thức gần đúng cho hai pha trên rồi so sánh chúng để tìm ra tiêu chuẩn phán đoán nước va rơi vào pha nào rồi dùng công thức thích hợp để tính.

Khi tính toán gần đúng coi

1 theo khai triển gần đúng Taylo, vậy

2

công thức nghiệm nước va cuối pha thứ nhất (14-16) là:

1 1



1 



(1 1 ) 

1



1

( 

1 ) 



1



0 21

2.2

2 0 2

2

2 1 

0 1

(14-21)

1 1 1

( 0 ) 1

1 0 

Cũng tương tự gần đúng cho nước va pha giới hạn ta có:

m 

2

2 

(14-22)

- Điều kiện xảy ra nước va là pha thứ nhất khi:

- Điều kiện xảy ra nước va là pha giới hạn khi:

1 > m

1 < m

hay 0 1 ; hay 0 1 .

Như vậy để xác định áp lực nước va lớn nhất, trước tiên ta dùng các công thức trên để phán đoán pha, nếu rơi vào pha thứ nhất thì dùng công thức (14-19) để tính còn nếu rơi vào pha giới hạn thì dùng công thức (14-20) để tính.

Chú ý rằng: các công thức tính ở trên phù hợp với turbine xung kích, tuy nhiên đối với turbine phản kích, quy luật đóng mở phức tạp giữa độ mở và lưu lượng không theo quy luật tuyến tính. Do vậy tính toán trên chỉ là gần đúng, để tính đúng xin xem phần tính theo phương pháp đồ giải. Trong phương pháp giải tích, nhà khoa học người Nga G.I. Kriptrenko đưa thêm vào các công thức (14-21) và (14-22) hệ số hiệu chỉnh để đề cập đến quy luật đóng mở của turbine phản kích như sau:

1 

2

1 2 b( 0)

(14-21')

m 

2

2 b

(14-22')

Trong đó, hệ số hiệu chỉnh b lấy như sau:

.Trường hơp đóng turbine: b = 0,7 - ( nS/1000);

.Trường hợp mở turbine: b + 1,1 - (nS/600).

3. Tính toán nước va trong ống phức tạp

Phầ trên chúng ta đã xét phương pháp tính toán áp lực nước va trong đường ống

đơn giản, trong đó các đặc trưng của nước va là c,

, 

không thay đổi theo chiều dài

ống và ống không có rẻ nhánh, trong thực tế thuỷ điện khi chiều dài đường ống dài, cột nước cao cần phải thay đổi đường kính, chiều dày thành ống, thậm chí vật liệu làm ống và cuối đường ống lại phân nhánh vào các tổ máy ... với mục đích về kinh tế. Đường ống phức tạp là ống có các đặc trưng nước va và kích thước thay đổi theo từng đoạn ống. Trong thực tế thường có hai dạng ống phức tạp hay gặp sau:

- Đường ống có đường kính giảm dần từ trên xuống, không rẽ nhánh;

- Đường ống có đường kính giảm dần từ trên xuống và córẽ nhánh.

Việc tính toán chính xác loại đường ống này rất phức tạp, phương pháp giải tích thường ta đưa về đường ống đơn giản tương đương có các đặc trưng trung bình c, V, , , ...và vẫn dựa vào các công thức ống đơn để tính gần đúng.

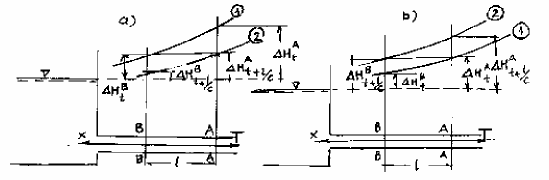
Hình 14-8. Sơ đồ tính nước va ống phức tạp và vẽ biểu đồ áp lực nước va dọc ống.

* Trường hợp 1: đường ống có chiều dày  , đường kính D và vật liệu làm ống thay đổi theo chiều dài ống, không rẽ nhánh (hình 14-8,a) có n đoạn ống như hình. Ta đưa về ống đơn giản tương đương có các đặc trưng sau:

n

Vi max . Li

n

Li

c V

n

Li. Vmax

n

2 Li

V max i1; c i1; max; i1; t f i1

n



Li

n Li

2g H0

g H0 Tsc

i1

i1 ci

Có các đặc trưng trung bình trên thay vào các công thức của ống đơn ta sẽ tính ra áp lực nước va của đường ống phức tạp cần tìm.

* Trường hợp 2:ống có rẽ nhánh (hình 14-8,a'):

Để tính áp lực nước va trong ống có rẽ nhánh về ống không rẽ nhánh có đặc tính thay đổi, giữ nguyên các đoạn ống chính và cắt bỏ đoạn ống nhánh cụt, các nhánh song song thay bằng một đoạn ống duy nhất. Ghép các đoạn ống nhánh lại trên cơ sởbảo toàn chiều dài và tổng diện tích ống nhánh, bảo toàn tốc độ truyền sóng c trên các nhánh. Ví dụ trên (hình 14-8,a') cần xác định áp lực nước va khi thay đổi độ mở turbine số 1 và 2 khi turbine số 3 đóng hoàn toàn ( ống nhánh số 3 là nhánh cụt) thì sơ đồ tính toán chuyển thành trường hợp 1, nhưng ở đây đoạn ống nhánh tương đương có chiều dài L1 và diện tích 2F1, tốc độ truyền sóng c = c1 (với hai ống nhánh như nhau). Sau đó ta tính như đã trình bày ở trường hợp 1.

4. Vẽ biểu đồ áp lực nước va dọc theo tuyến ống

Mục đích của việc vẽ biểu đồ áp lực nước va (+) lớn nhất là để xác định áp lực nước (bao gồm cột nước tĩnh cộng với áp lực nước va) tại các mặt cắt ống. Do vậy mực nước ở hồ hoặc bể áp lực phải lấy MNDBT và không trừ tổn thất cột nước (hình 14- 8,b).

Mục đích vẽ biểu đồ áp lực nước va âm là kiểm tra xem biểu đồ này có chỗ nào chạm vào ống (tức chỗ ấy có chân không trong ống). Nếu chạm thì tốt nhất là hạ chiều cao ống xuống dưới biểu đồ hoặc xử lý bằng đai cứng để bảo đảm ổn định thành ống. Do vậy mực nước hồ hoặc mực nước trong bể áp lực lấy MNC và có trừ tổn thất cột nước (hình 14-8,b).

Để vẽ biểu đồ áp lực nước va dọc ống ta trải đường ống theo chiều dài. Tại mặt cắt cuối ống (A-A) ta tính trị số nước va dương HA và nước va âm HA , còn tại mặt cắt B-B sát hồ HB0 . Coi như áp lực nước va dọc ống phân bố theo quy luật

đường thẳng, ta nối hai đầu ta được biểu đồ phân bố áp lực nước va trải dọc theo ống. Có trị số áp lực tại các vị trí đặt lên mặt cắt C-C, A-A, B-B ta được biểu đồ áp lực nước va dọc ống (hình 14-8,b). Trường hợp có buồng điều áp ta cũng làm tương tự và thể hiện biểu đồ áp lực nước va như (hình 14-8,).

Chú ý rằng thực tế sự phân bố áp lực nứơc va dọc ống phụ thuộc vào đặc tính đường ống và độ mở ban đầu của CCHD hay van kim, do vậy thực tế coi phân bố áp lực theo đường thẳng là gần đúng. Thực tế, nếu trạng thái nước va là pha thứ nhất thì quy luật phân bố áp lực nước va dọc ống là đường cong lõm, còn trạng thái pha giới hạn thì lại gần đường thẳng, như đường cong nét đứt trên (hình 14-8,).

XIV. 2. 3. Tính toán nước va bằng phương pháp đồ giải

Như trên đã thấy phương pháp giải tích chỉ phù hợp với turbine xung kích mà không thích hợp đầy đủ đối với turbine phản kích, bởi lẻ ở turbine phản kích lưu lượng qua turbine trong quá trình chuyển tiếp rất phức tạp, nó phụ thuộc vào nhiều yếu tố như

đặc tính độ mở

a 0 của cánh hướng dòng, phụ thuộc vào vòng quay, vào góc xoay trong

turbine cánh quay ..v.v... Những yếu tố này không thể hiện được bằng toán học mà bằng

đường đặc tính tổng hợp chính - xây dựng trên cơ sở thí nghiệm. Ngoài ra, dùng phương