Công Thức Tính Bậc Tự Do Của Cơ Cấu Phẳng

Ngoài ra, trong số các bậc tự do được tính theo công thức (1.2), có thể có những bậc tự do không có ý nghĩa đối với vị trí các khâu động trong cơ cấu, nghĩa là không ảnh hưởng gì đến cấu hình của cơ cấu. Các bậc tự do này gọi là bậc tự do thừa và phải loại đi khi tính toán bậc tự do của cơ cấu.

Tóm lại, công thức tổng quát để tính bậc tự do là:

W= 6n – ( jp j - Rtrùng - Rthừa) - Wthừa (1.3)

Với Rrung : số ràng buộc trùng; Rthừa: số rằng buộc thừa; Wthừa: số bậc tự do thừa.

1.2.2. Công thức tính bậc tự do của cơ cấu phẳng

a. Với cơ cấu phẳng

Ngay khi còn để rời nhau trong hệ quy chiếu gắn liền với giá, các khâu được xem như nằm trên cùng một mặt phẳng (hay trên các mặt phẳng song song nhau). Do đó tổng số bậc tự do của n khâu động: W0 = 3n

Có thể bạn quan tâm!

Xem toàn bộ 167 trang tài liệu này.

Gọi Oxy là mặt phẳng chuyển động của cơ cấu thì các bậc tự do Tz, Qx, Qy của

mỗi khâu đã bị hạn chế.

Mỗi khớp quay có trục quay Oz vuông góc với mặt phẳng Oxy chỉ còn hạn chế hai bậc tự do là chuyển động tịnh tiến Tx và Ty.

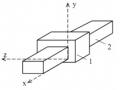
Mỗi khớp trượt có phương trượt nằm trong mặt phẳng Oxy (hình 1.21) chỉ còn

hạn chế hai bậc tự do là chuyển động quay Qz và chuyển động tịnh tiến TN trong mặt phẳng Oxy theo phương vuông góc với phương trượt.

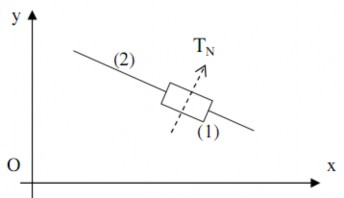
Hình 1.21. Khớp trượt

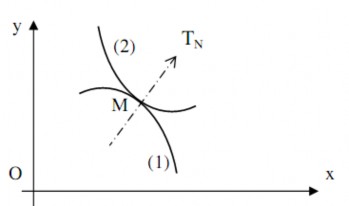
Mỗi khớp cao loại 4 như khớp bánh răng phẳng, khớp cam phẳng (hình 1.22) chỉ còn hạn chế một bậc tự do là chuyển động tịnh tiến TN trong mặt phẳng Oxy theo phương pháp tuyến chung của hai thành phần khớp cao.

Trong cơ cấu phẳng thường chỉ dùng ba loại khớp trên nên tổng số các ràng buộc do các khớp trong cơ cấu phẳng tạo ra: R = 2p5 + p4

Như vậy, bậc tự do của cơ cấu:

W = 3n – (2p5 + p4) (1.4)

Thông thường có thể dùng công thức (1.4) để tính bậc tự do của cơ cấu.

Ví dụ

Hình 1.22. Khớp cam phẳng

Cơ cấu 4 khâu bản lề phẳng (hình 1.20): n=3, p5 =4; p4= 0 => W= 3.3- (2.4 +0) = 1.

Tuy nhiên, kể đến các ràng buộc trùng, ràng buộc thừa và bậc tự do thừa, công

thức tổng quát để tính bậc tự do của cơ cấu phẳng như sau:

W= 3n – (2p5 + p4 – Rtrùng - Rthừa ) - Wthừa (1.5)

b. Ví dụ về rằng buộc trùng

Trong cơ cấu phẳng, ràng buộc trùng chỉ có tại các khớp đóng kín của đa giác gồm 3 khâu nối với nhau bằng 3 khớp trượt.

Ví dụ

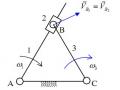
Xét cơ cấu trên hình 1.23.

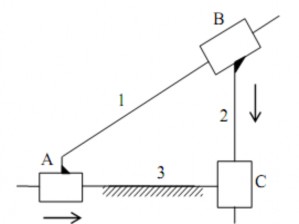
Hình 1.23. Ràng buộc trùng

Giả sử lấy khớp B làm khớp đóng kín. Khi nối khâu 3 với khâu 1 và khâu 2 bằng các khớp A và C, khâu 2 không thể quay tương đối so với khâu 1 quanh trục Oz (trục Oz vuông góc với mặt phẳng chuyển động của cơ cấu), tức là có một ràng buộc gián tiếp Qz giữa khâu 1 và khâu 2 (hình 1.24).

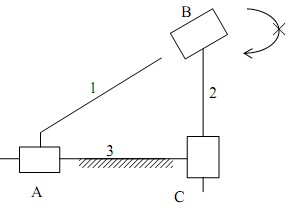
Hình 1.24. Sơ đồ tháo khớp

Khi nối trực tiếp khâu 1 và khâu 2 bằng khớp đóng kín B, khớp B lại tạo thêm ràng buộc Qz. Như vậy, ở đây có một ràng buộc trùng: Rtrùng = 1. Tóm lại, bậc tự do của cơ cấu ( n=2, p5 =3, p4=0).

c. Ví dụ về rằng buộc thừa

Xét hệ cho trên hình 1.25: n =4, p5 =6. Bậc tự do của hệ tính theo công thức (1.4): W=3n – (2p5 +p4) = 3.4 – (2.6 + 0) = 0.

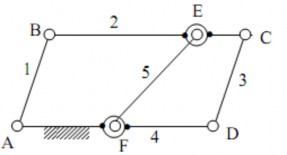
Hình 1.25. Cơ cấu có ràng buộc thừa

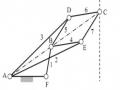
Điều này có nghĩa hệ đã cho là một khung tĩnh định. Tuy nhiên nến thay đổi cấu trúc hệ như hình 1.26 với kích thước động thỏa mãn điều kiện: lAB = lCD = lEF; lAF = lBE; lBC= lAD thì hệ sẽ chuyển động được và thực sự là một cơ cấu, tức là bậc tự do thực của hệ phải lớn hơn 0.

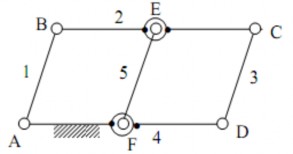
Hình 1.26. Cơ cấu hình bình hành

Điều này được giải thích như sau: Khi chưa nối khâu 2 và khâu 4 bằng khâu 5 và hai khớp quay E, F thì hệ là một cơ cấu bốn khâu bản lề phẳng có bậc tự do W =1, có lược đồ là một hình bình hành ABCD. Do đặc điểm hình học của cơ cấu, khoảng cách

giữa hai điểm E của khâu 2 và điểm F của khâu 4 với lAF = lBE luôn luôn không đổi khi cơ cấu chuyển động. Thế mà việc nối điểm E của khâu 2 và điểm F của khâu 4 bằng khâu 5 và hai khớp quay E, F chỉ nhằm mục đích giữ cho hai điểm E và F cách nhau một khoảng không đổi, nên ràng buộc do khâu 5 và hai khớp quay E, F là ràng buộc thừa. Mặt khác, khi thêm khâu 5 và hai khớp quay E, F vào cơ cấu sẽ tạo thêm cho cơ cấu một bậc tự do bằng (n =1, p5= 2):

W = 3n – (2p5 +p4) =3.1 -2.2 = -1, tức là tạo ra một ràng buộc. Như vậy số ràng buộc

thừa trong trường hợp này sẽ bằng: Rthừa =1.

Tóm lại, bậc tự do của cơ cấu như hình 1.26: W = 3n - (2p5 +p4 - Rthừa) = 3.4 – (2.6 +0-1) =1.

d. Ví dụ về bậc tự do thừa

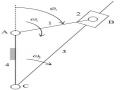
Trong cơ cấu cam cần lắc đáy lăn (dùng để biến chuyển động quay liên tục của cam 1 thành chuyển động lắc qua lại theo một quy luật cho trước của cần 3 (hình 1.27).

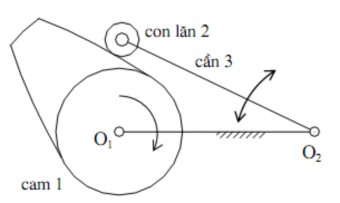
Hình 1.27. Cơ cấu cam cần lắc đáy lăn

Ta có n=3, p5 =3 ( ba khớp quay loại 5); p4=1 ( một khớp cam phẳng loại 4). Bậc tự do của hệ tính theo công thức (1.4): W =3.3 – (2.3 +1) =2.

Tuy nhiên, bậc tự do của cơ cấu: W =1, bởi vì khi cho cam quay đều thì chuyển động của cần hoàn toàn xác định. Ở đây có một bậc tự do thừa: Wthừa = 1, đó là chuyển động quay của con lăn xung quanh trục của mình, bởi vì khi cho con lăn quay xung quanh trục này, cấu hình của cơ cấu hoàn toàn không đổi.

Tóm lại, bậc tự do của cơ cấu: W =3n – (2p5 + p4) - Wthừa= 3.3- (2.3 +1) -1 =1.

1.2.3. Khâu dẫn – Khâu bị dẫn – Khâu phát động

a. Khâu dẫn

Khâu dẫn là khâu có thông số vị trí cho trước (hay nói khác đi, có quy luật chuyển động cho trước). Ví dụ trong cơ cấu 4 khâu bản lề hình 1.20, khâu dẫn là khâu 1 có quy luật chuyển động υ1 = υ1(t) cho trước. Thông thường, khâu dẫn được chọn là khâu nối với giá bằng khớp quay và chỉ cần một thông số để xác định vị trí của nó. Thế mà, số bậc tự do của cơ cấu là thông số vị trí cần cho trước để vị trí của cơ cấu

hoàn toàn xác định, do đó thông thường cơ cấu có bao nhiêu bậc tự do sẽ cần có bấy nhiêu khâu dẫn.

b. Khâu bị dẫn

Ngoài giá và khâu dẫn ra, các khâu còn lại được gọi là khâu bị dẫn. Khái niệm khâu dẫn, khâu bị dẫn không có ý nghĩa đối với các cơ cấu rô bốt. Trong các cơ cấu này, không có khâu nào mà chuyển động hoàn toàn phụ thuộc vào chuyển động của một hay một số khâu khác, chuyển động của mỗi khâu được điều khiển bằng một kích hoạt riêng biệt.

c. Khâu phát động

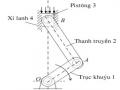
Khâu phát động là khâu được nối trực tiếp với nguồn năng lượng làm cho máy chuyển động. Ví dụ, với động cơ đốt trong hình 1.1, khâu phát động là pistông. Còn khâu dẫn thường được chọn là khâu có vận tốc góc không đổi hay theo yêu cầu làm việc phải có vận tốc góc không đổi, ở đây chọn trục khuỷu làm khâu dẫn.

Khâu phát động có thể trùng hay không trùng với khâu dẫn, tuy nhiên thông thường người ta chọn khâu dẫn trùng với khâu phát động

1.3. Xếp hạng cơ cấu phẳng

1.3.1. Nhóm Atxua – Hạng của nhóm

a. Nhóm tĩnh định

Xét cơ cấu bốn khâu bản lề ABCD (hình 1.28).

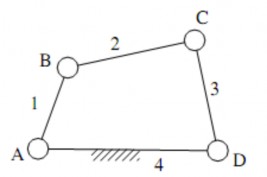
Hình 1.28. Cơ cấu 4 khâu bản lề

Tách khỏi cơ cấu khâu dẫn 1 và giá 4, sẽ còn lại một nhóm gồm hai khâu 2 và 3 nối với nhau bằng khớp quay C (hình 1.29).

Ngoài ra trên mỗi khâu còn một thành phần khớp và được gọi là khớp chờ: khớp chờ B và khớp chờ C. Như vậy nhóm còn lại gồm có hai khâu (n=2) và ba khớp quay ( p5=3), bậc tự do của nhóm: W = 3.2 -2.3 = 0. Đây là một nhóm tĩnh định vì khi cho trước vị trí của các khớp chờ thì vị trí của khớp trong C hoàn toàn xác định.

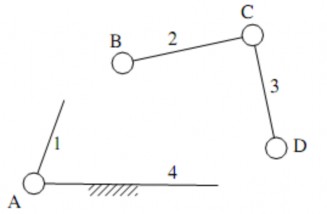
Hình 1.29. Sơ đồ tách nhóm tĩnh định

Vậy nhóm tĩnh định là nhóm có bậc tự do bằng 0 và không thể tách thành các nhóm nhỏ hơn có bậc tự do bằng 0.

b. Hạng của nhóm tĩnh định

+ Nhóm tĩnh định chỉ có hai khâu và ba khớp được gọi là nhóm Atxua hạng II. Có năm loại nhóm Atxua hạng II như sau ( hình 1.30):

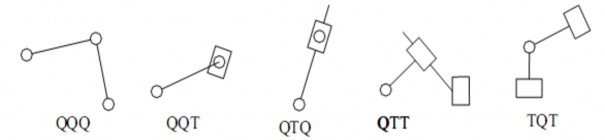
Nhóm gồm có hai khâu và ba khớp trượt không phải là một nhóm tĩnh định vì bậc tự do của nhóm bằng 1.

+ Nhóm Atxua có hạng cao hơn II

Nếu các khớp trong của một nhóm tĩnh định tạo thành một đa giác thì hạng của nhóm Atxua được lấy bằng số đỉnh của đa giác, nếu tạo thành nhiều đa giác thì hạng của nhóm lấy bằng số đỉnh của đa giác nhiều đỉnh nhất.

Ví dụ

Cơ cấu trên hình 1.31.

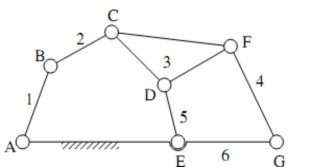
Hình 1.31. Cơ cấu 6 khâu bản lề

Cơ cấu trên có thể tách thành khâu dẫn 1 nối giá bằng khớp và một nhóm tĩnh định BCDEFG (hình 1.32).

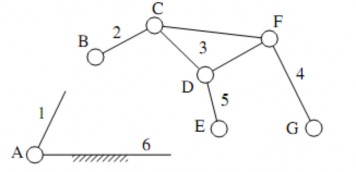
Hình 1.32. Sơ đồ tách nhóm tĩnh định

Các khớp chờ là khớp B, E, G. Các khớp trong là khớp C, D, F. Nhóm này có một đa giác khép kín là CDF có ba đỉnh nên là nhóm hạng III.

1.3.2. Hạng của cơ cấu

+ Cơ cấu hạng I là cơ cấu có một khâu động nối với giá bằng khớp quay, ví dụ cơ cấu roto máy điện.

+ Cơ cấu có số khâu động lớn hơn 1 có thể coi là tổ hợp của một hay nhiều cơ cấu hạng I với một số nhóm Atxua. Nếu cơ cấu chỉ có một nhóm Atxua thì hạng của cơ cấu là hạng của nhóm. Nếu cơ cấu có nhiều nhóm Atxua thì hạng của cơ cấu lấy bằng hạng của nhóm Atxua có hạng cao nhất. Ví dụ cơ cấu trên hình 1.31 là cơ cấu hạng III.

Việc xếp hạng cơ cấu có ý nghĩa thiết thực trong việc nghiên cứu một số bài tính động học và lực học của cơ cấu.

BÀI TẬP CHƯƠNG 1

Bài 1: Tính bậc tự do của cơ cấu động cơ đốt trong kiểu chữ V (hình 1.33).

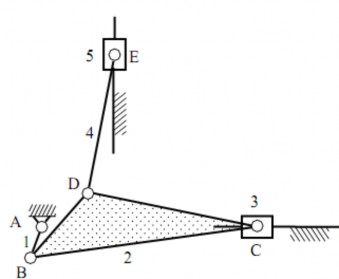
Hình 1.33

Bài 2: Tính bậc tự do của cơ cấu chuyển động theo quỹ đạo cho trước (hình 1.34).

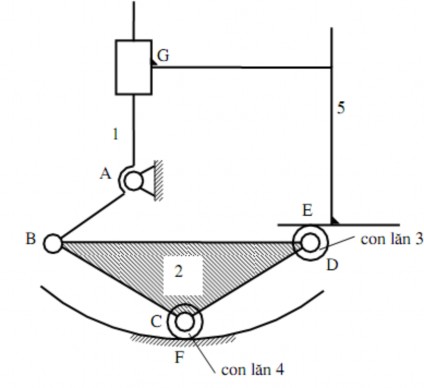
Hình 1.34

Bài 3: Tính bậc tự do của cơ cấu vẽ đường thẳng của Lipkin (hình 1.35).

Cho lAD = lAE; lBD = lDC = lCE = lEB; lAF =lFB