Phân Biệt Suy Luận Diễn Dịch, Ngoại Suy Và Quy Nạp Trong Toán Học

Theo nhà Tâm lý học người Nga V. A. Cruchetxki [10]: “Năng lực được hiểu như là một phức hợp các đặc điểm tâm lí cá nhân của con người đáp ứng những yêu cầu của một loạt hành động nào đó và là điều kiện thành công hoạt động đó”.

Xavier Roegiers khẳng định: Năng lực là sự tích hợp các kĩ năng tác động một cách tự nhiên lên các nội dung trong một loại tình huống cho trước để giải quyết những vấn đề do những tình huống này đặt ra [30].

Theo Phạm Minh Hạc [12]: “Năng lực chính là một tổ hợp các đặc điểm tâm lí của một con người (còn gọi là tổ hợp thuộc tính tâm lí của một nhân cách), tổ hợp đặc điểm này vận hành theo một mục đích nhất định tạo ra kết quả của một hoạt động nào đấy”.

Như vậy, có nhiều quan điểm khác nhau về năng lực nhưng đều có những đặc điểm chung như sau:

Năng lực là khả năng thực hiện thành công, giải quyết các vấn đề trong các tình huống cụ thể. Năng lực chịu sự tác động của các yếu tố như bẩm sinh di truyền, môi trường và hoạt động của bản thân.

Điều kiện cần thiết để hình thành và phát triển năng lực là tri thức và kĩ năng. Bởi, “năng lực của mỗi người dựa trên cơ sở tư chất, nhưng điều chủ yếu là năng lực hình thành, phát triển và thể hiện trong hoạt động tích cực của con người dưới sự tác động của rèn luyện, dạy học và giáo dục” [18].

1.2.2. Năng lực toán học

Năng lực toán học là một hình thức năng lực chuyên môn, gắn liền với bộ môn toán học. Có nhiều quan niệm khác nhau về năng lực toán học.

Theo Blohm & Jensen (2007): “Năng lực toán học là khả năng sẵn sàng hành động để đáp ứng với thách thức toán học của các tình huống nhất định”.

Theo Niss Mogens(1999): “Năng lực toán học như khả năng của cá nhân để sử dụng các khái niệm toán học trong một loạt các tình huống có liên quan đến toán học, kể cả những lĩnh vực bên trong hay bên ngoài của toán học (để hiểu, quyết định và giải thích)”.

Niss Mogens cǜng xác định tám thành tố của năng lực toán học và chia thành hai

cụm. Cụm thứ nhất bao gồm: năng lực tư duy toán học; năng lực giải quyết vấn đề toán

học; năng lực mô hình hóa toán học; năng lực suy luận toán học. Cụm thứ hai bao gồm: năng lực biểu diễn, năng lực sử dụng ngôn ngữ và kí hiệu hình thức; năng lực giao tiếp toán học; năng lực sử dụng công cụ, phương tiện học toán.

Tám năng lực này có mối quan hệ chặt chẽ với nhau và là những năng lực cần thiết để cá nhân có thể học tập, ứng dụng môn toán.

Theo tác giả Trần Kiều (2014): “Các năng lực cần hình thành và phát triển cho người học thông qua dạy học môn Toán trong trường phổ thông Việt Nam là: năng lực tư duy; năng lực giải quyết vấn đề; năng lực mô hình hóa toán học; năng lực giao tiếp; năng lực sử dụng công cụ, phương tiện toán học; năng lực học tập độc lập và hợp tác” [26].

Một trong những mục tiêu chung của Chương trình giáo dục phổ thông môn Toán (Ban hành kèm theo thông tư số 32/2018/TT-BGDĐT ngày 26 tháng 12 năm 2018 của Bộ trưởng Bộ Giáo dục và Đào tạo) là hình thành và phát triển năng lực toán học bao gồm các thành tố cốt lòi: năng lực tư duy và lập luận toán học; năng lực mô hình hoá toán học; năng lực giải quyết vấn đề toán học; năng lực giao tiếp toán học; năng lực sử dụng công cụ, phương tiện học toán.

1.3 Suy luận

1.3.1 Khái niệm

Theo lôgic học của tác giả Nguyễn Như Hải thì suy luận là hình thức lôgic của tư duy trong đó các phán đoán được liên kết lại với nhau để rút ra phán đoán mới.

Mỗi suy luận được biểu diễn dưới dạng một mệnh đề kéo theo mà tiền đề là một mệnh đề hoặc hội của nhiều mệnh đề: A1, A2,… An B (các Ai là các tiền đề, B là kết luận). [15]

Bất kǶ suy luận nào cǜng bao gồm tiền đề, lập luận và kết luận. [14]

Tiền đề: là một hay một số phán đoán đã được thực tiễn thừa nhận hoặc được khoa học chứng minh là đúng. Trên cơ sở giá trị đúng của các tiền đề có thể rút ra các phán đoán mới, chứa đựng tri thức mới mà bản thân riêng rẽ từng tiền đề không thể có được.

Lập luận: là phương pháp logic rút ra kết luận từ các tiền đề. Các phương pháp logic này không chỉ thể hiện trình tự sắp xếp các phán đoán thuộc tiền đề mà còn bao

gồm cả những quy luật mà những quy tắc logic chi phối trình tự sắp xếp để đưa ra phán đoán mới một cách tất yếu.

Kết luận: là phán đoán mới thu được từ các tiền đề thông qua lập luận. Kết luận có nhiều dạng khác nhau, có kết luận phù hợp, có kết luận không phù hợp với hiện thực khách quan, có kết luận là ngẫu nhiên, có kết luận là tất yếu từ những lập luận logic của các tiền đề.

Trong tiếng Việt, phán đoán đứng trước các từ “nên”, “cho nên”, “do đó”, “vì vậy”, “suy ra”… và đứng sau các từ “vì”, “bởi vì”, … là tiền đề. Ngược lại, phán đoán đứng sau các từ “nên”, “cho nên”, “do đó”, “vì vậy”,… và đứng trước các từ “vì”, “bởi vì”,… là kết luận. Nắm vững cách biểu thị đó giúp chúng ta nhận biết nhanh chóng tiền đề và kết luận khi phân tích bất cứ một suy luận nào.

Căn cứ vào cách thức lập luận, suy luận được chia ra thành suy luận diễn dịch, suy luận quy nạp và suy luận ngoại suy.

1.3.2 Các loại suy luận

Peirce (1994) cho rằng có 3 loại suy luận cơ bản: diễn dịch, quy nạp và ngoại suy.

Chúng tôi minh họa các loại suy luận qua ví dụ sau [24] [25]:

Diễn dịch

Quy luật: Nếu hình thoi có một góc vuông thì nó là hình vuông

Trường hợp: Hình thoi ABCD có một góc vuông

Kết luận: Hình thoi ABCD là hình vuông

Quy nạp

Trường hợp: Hình thoi ABCD có một góc vuông

Kết luận: Hình thoi ABCD là hình vuông

Quy luật: Nếu hình thoi có một góc vuông thì nó là hình vuông

Ngoại suy

Quy luật: Nếu hình thoi có một góc vuông thì nó là hình vuông

Kết luận: Hình thoi ABCD là hình vuông

Trường hợp: Hình thoi ABCD có một góc vuông

Ví dụ này cho thấy, trong khi suy luận suy diễn tìm kiếm các kết luận từ những kết quả đúng cho trước; suy luận quy nạp tìm kiếm kết quả tổng quát cho các kết quả đúng của những trường hợp riêng; còn suy luận ngoại suy tìm kiếm lời giải thích tốt nhất cho những kết quả có trước.

Phép suy luận ngoại suy như ở ví dụ trên không đúng về mặt phân tích hoặc suy luận logic hình thức vì có thể xét các trường hợp khác như hình thoi ABCD có hai đường chéo bằng nhau hoặc có hai góc kề bằng nhau. Tuy nhiên dạng suy luận này chứa đựng cách thức mà con người lý giải khi thực hiện các khám phá, khảo sát. Ngoại suy tìm kiếm hoặc hình thành các giả thuyết, lý thuyết có thể giải thích một sự kiện (gây ngạc nhiên) hoặc một quan sát (gây bất ngờ). Như thế ngoại suy tạo ra các ý tưởng mới và giúp mở rộng tri thức [25].

1.3.3 Phân biệt suy luận diễn dịch, ngoại suy và quy nạp trong toán học

Dựa trên các cơ sở lí thuyết chung về suy diễn, quy nạp, ngoại suy đã trình bày ở trên ta có thể phân biệt ba loại suy luận trên theo các yếu tố sau [14]:

a) Điều kiện để xảy ra và kết quả của ba loại suy luận

Nếu ta có một quy tắc“Nếu P thì Q”, một Sự kiện P và một Hệ quả Q thì: Cho trước thông tin về mối quan hệ giữa P và Q, quy nạp suy ra Quy tắc: “Nếu P thì Q”.

Cho trước thông tin về P và Quy tắc: “Nếu P thì Q”, diễn dịch suy ra Hệ quả Q. Cho trước Quy tắc: “Nếu P thì Q” và Hệ quả Q, ngoại suy suy ra Giả thuyết: “có thể là P”.

Chú ý rằng với ngoại suy, có thể xảy ra một trong các trường hợp sau:

Trường hợp 1: Ngoài quy tắc “Nếu P thì Q”, nếu trong tri thức có sẵn của người học có thêm một số quy tắc: “Nếu K thì Q”, “Nếu H thì Q”… thì ngoại suy có nhiệm vụ chọn ra một giả thuyết có lí nhất trong các giả thuyết “có thể là P”, “có thể là H”, “có thể là K”. Ngoại suy trong trường hợp này được xếp vào loại ngoại suy chọn lựa.

Ví dụ 1.3 Đây là ví dụ được Reid (2003) sử dụng để minh họa cho suy luận ngoại suy xảy ra trong lớp học toán. Trong ví dụ này một GV ở Pháp đang hướng dẫn một lớp

học ở cấp độ 4 (HS tuổi từ 13 đến 14) chứng minh định lý Pytago. Các em đã kết luận được ABCD là hình thoi vì chúng có 4 cạnh bằng nhau. Sau đây là đoạn trao đổi giữa GV và HS [25]:

GV: ABCD là hình thoi, chúng ta đã có đủ yếu tố để kết luận, không cần thêm điều gì nữa. Nhưng đó không phải là những gì thầy yêu cầu các em chứng minh. Thầy muốn các em chứng mình rằng nó là…

HS: Hình vuông.

GV: Đúng rồi, hình vuông. Vậy thì với điều kiện nào nữa thì ABCD là hình vuông.

Điều kiện nào thì hình thoi ABCD là hình vuông?

Nhiều HS: Nếu nó có 1 góc vuông. GV: Nếu nó có…?

Nhiều HS: 1 góc vuông.

GV: 1 góc vuông, vậy là đủ.

Ở đây ta có một sơ đồ ngoại suy sau:

Kết luận: ABCD là hình thoi, ABCD là hình vuông.

Quy tắc: Nếu hình thoi có một góc vuông thì nó là hình vuông.

Trường hợp: ABCD có một góc vuông.

Trong tình huống này thứ nhất là sự hiện diện của hai kết luận: một kết luận đã có sẵn từ giả thiết của bài toán và một kết luận được đề xuất dựa trên quan sát hình vẽ và yêu cầu của GV. Đây là một phần của “hợp đồng didactic” rằng kết luận mà GV muốn HS chứng minh là đúng. Thứ hai là có nhiều Quy tắc khác nhau mà HS có thể chọn lựa, chẳng hạn “nếu hình thoi có hai đường chéo bằng nhau thì đó là hình vuông”, hoặc “nếu hình thoi có hai góc kề bằng nhau thì đó là hình vuông”. Sử dụng một trong các Quy tắc này có thể sẽ hữu ích hoặc không hữu ích cho việc chứng minh của HS. Nói cách khác, HS cần chọn một giả thuyết “tốt nhất” dựa trên các yếu tố đã có sẵn của bài toán. Theo Eco, phép ngoại suy mà HS sử dụng trong trường hợp này là ngoại suy chọn lựa [25].

Trường hợp 2: Nếu Quy tắc “Nếu P thì Q” có chiều ngược lại “Nếu Q thì P” thì giả thuyết ngoại suy không chỉ là một giả thuyết có lí, mà nó còn là giả thuyết đúng và duy nhất: “Chắc chắn là P”. Ngoại suy trong trường hợp này là ngoại suy trực tiếp

theo cách phân loại của Eco (1983) [25] [35].

Trường hợp 3: Nếu Quy tắc “Nếu P thì Q” chưa tồn tại trong tri thức người học, thì việc suy ra đồng thời Quy tắc “Nếu P thì Q” và Giả thuyết: “có thể là P” là kết quả của ngoại suy sáng tạo [25].

Bảng 1.2. Mô hình so sánh ba loại suy luận

Diễn dịch

Quy nạp

Ngoại suy

Quy tắc: i : C ( xi) R ( xi)

Trường hợp: C ( x0 )

Kết luận: R ( x0 )

Trường hợp: C ( x0 )

Kết luận: R ( x0 ) Quy tắc: i : C ( xi) R ( xi)

Kết luận: R ( x0 )

Quy tắc: i : C ( xi) R ( xi)

Trường hợp: C ( x0 )

Có thể bạn quan tâm!

Xem toàn bộ 143 trang tài liệu này.

b) Mục đích tiến hành mỗi loại suy luận

Suy luận diễn dịch sử dụng các quy tắc lôgic toán và các tiên đề đã biết để khẳng định sự đúng đắn của một kết quả và thường sử dụng trong quá trình chứng minh toán học.

Suy luận quy nạp giúp tổng quát hóa một kết quả từ các trường hợp riêng tương tự nhau, nhằm mở rộng phạm vi áp dụng của một tính chất/một tri thức toán cho một nhóm đối tượng lớn hơn. Quy nạp thường được sử dụng trong khám phá các kết quả mang tính tổng quát. Quy nạp cǜng được dùng để hỗ trợ cho phương án giải quyết vấn đề, giải quyết một bài toán đơn giản hơn bằng cách hạn chế lại số trường hợp cần xem xét và sau đó dùng suy luận quy nạp để tổng quát hóa kết quả cho bài toán chính.

Suy luận ngoại suy nhằm đưa ra một giả thuyết có thể chấp nhận được để lý giải cho một hiện tượng hoặc quan sát gây ngạc nhiên trong quá trình khám phá các tri thức toán. Ngoại suy cǜng được dùng để định hướng cho quá trình chứng minh bằng cách suy luận ngược từ điều cần chứng minh (các kết luận) đến giả thiết mà bài toán cho sẵn (các trường hợp) [24] [25].

c) Khám phá toán và tính chắc chắn của kết quả

Tính chắc chắn của những kết luận được tạo ra bởi các loại suy luận này giảm dần từ diễn dịch đến quy nạp và cuối cùng là ngoại suy. Bản chất “tạo ra chân lí” của

diễn dịch luôn luôn tạo ra một kết luận có cơ sở vững chắc vì những tiên đề đúng luôn luôn đưa đến những kết luận đúng. Kết luận được suy ra không phải là sự tổng quát hóa vì thế không cần có sự xác minh thực nghiệm. Trái lại, ngoại suy và quy nạp tạo ra các kết luận dựa trên thực nghiệm và có thể là sai [25].

Tuy nhiên, xét về khía cạnh khám phá tri thức mới, những tri thức có được từ suy luận diễn dịch có thể xem như những hệ quả lôgic được suy ra từ những tiên đề đúng đã biết trước, do đó chúng không thể mở rộng vốn tri thức sẵn có của con người. Với quy nạp, tri thức mới thu được dưới dạng tổng quát hóa, là mở rộng phạm vi của những tri thức đã biết theo các xu hướng có thể đoán trước được. Với ngoại suy, khi những tri thức có sẵn không giải thích được cho quan sát, tri thức mới được hình thành. [25] [42].

1.3.4. Một số quy tắc suy luận cơ bản

Các loại tam đoạn luận:

- Tam đoạn luận khẳng định: X Y , X

- Tam đoạn luận phủ định: ( X Y )Y

- Tam đoạn luận lựa chọn: X Y , X

- Tam đoạn luận bắc cầu: X Y ,Y Z

X Z

Các quy tắc từ mệnh đề phổ biến:

x , P x, (a là x) hoặc (x , P x Q ( x)) , (a là x)

P(a) P a Q ( a)

Quy tắc quy nạp

Để kết luận P(n) đúng với mọi số tự nhiên n n0 , người ta dùng phép quy nạp như sau:

P ( no ) 1, (nếu P k  1,k n0 , thì

P(k+1)=1) P(n) đúng với mọi số tự nhiên n n0

1.4 Mô hình Toulmin

1.4.1 Cấu trúc của mô hình Toulmin

Lý thuyết tam đoạn luận của Aristotle là lý thuyết đầu tiên mô tả mô hình cấu trúc của lập luận. Cấu trúc này bao gồm: tiên đề lớn, tiên đề nhỏ và kết luận. Theo Platin, tam đoạn luận không khám phá được kiến thức mới vì kết luận của nó chứa trong các tiên đề.

Toulmin (1958) cho rằng lập luận chặt chẽ là kỹ năng cơ bản của con người sống trong thế kỉ XXI. Chính vì vậy, ông đã dành nhiều thời gian nghiên cứu về bản chất của quá trình lập luận, đặc biệt là lập luận toán học. Toulmin xem xét một lập luận gồm có ba thành tố cơ bản là: luận cứ, kết luận và luận chứng. Luận cứ (hay còn gọi là tiền đề) là một hoặc nhiều dữ kiện xuất phát làm căn cứ cho lập luận, từ đó để suy ra kết luận, nó trả lời cho câu hỏi “chứng minh bằng cái gì?”. Kết luận là một khẳng định có được trên cơ sở luận cứ đã cho, nó trả lời cho câu hỏi “chứng minh cái gì?”. Luận chứng là những quy tắc, nguyên lý, định lý,… mà nhờ đó từ tiền đề chúng ta suy ra kết luận, nó trả lời cho câu hỏi “chứng minh bằng cách nào?”. Ngoài ba thành tố cơ bản trên, Toulmin còn bổ sung thêm ba thành tố phụ nữa đó là: luận chứng bổ sung sử dụng trong trường hợp luận chứng ban đầu chưa đủ sức thuyết phục, miền bác bỏ xét xem trong trường hợp nào thì lập luận không còn đúng nữa và mức độ đáng tin của lập luận chẳng hạn như: chắc chắn đúng, có thể đúng, không thể [22] [49].

D (Data): Luận cứ C (Claim): Kết luận

W (Warrant): Luận chứng

Hình 1.4 Dạng cơ bản của mô hình Toulmin

Ví dụ 1.4 Để biểu diễn quy trình chứng minh ABC vuông tại đỉnh A, chúng ta sử dụng mô hình sau:

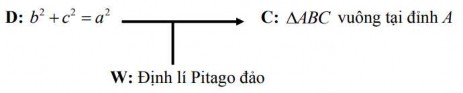
Hình 1.5 Mô hình Toulmin chứng minh ABC vuông