Một Minh Họa Về Biểu Diễn Toán

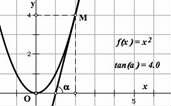
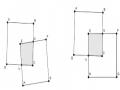
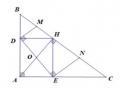
Bruner cǜng chỉ ra rằng có thể chia biểu diễn thành ba phạm trù từ thấp đến cao như sau [48]: + Thực tế: gồm các biểu diễn thực tế và các biểu diễn thao tác được.

+ Biểu tượng: các BDTQ sử dụng các hình ảnh, đồ thị, sơ đồ, biểu bảng...

+ Ký hiệu: gồm có biểu diễn ngôn ngữ và biểu diễn ký hiệu.

Trong ba phạm trù biểu diễn ở trên, BDTQ đóng vai trò trung gian nối kết biểu diễn thực tế với biểu diễn ký hiệu.

Bảng 1.1. Một minh họa về biểu diễn toán

Loại biểu

diễn

Ví dụ trong chủ đề đạo

Hàm

Đặc trưng

Biểu diễn ký hiệu

f (x)  x2  f '(2)  4

Rất chuẩn xác, ngắn gọn và rò ràng.

Biểu diễn

Đạo hàm của hàm số x2

Bị chi phối bởi các quy ước của ngôn

ngữ, thiếu sự cô đọng và ngắn gọn

ngôn ngữ

tại điểm x bằng 2 là 4.

nhưng mô tả được và tạo cảm giác quen

thuộc, dễ nhớ.

Biểu diễn minh họa, trực quan

Vì tương tự với đối tượng được biểu diễn nên loại biểu diễn này vừa trực quan vừa trực giác. Nếu được thiết kế trên máy tính thì sẽ thể hiện được quá trình trung gian.

Biểu diễn thực thao tác được

Mô hình tạo từ các vật liệu có thể uốn cong được. Thể hiện khá cụ thể, thực hiện được các thao tác lên đối tượng, độ chính xác chấp nhận được.

Biểu diễn thực tế

Mô hình mô tả chiếc xe đang chuyển động. Thể hiện sống động, rất cụ thể và tự nhiên.

Có thể bạn quan tâm!

Xem toàn bộ 143 trang tài liệu này.

Để học sinh có thể nhận thức được một khái niệm, cần kết hợp những biểu diễn khác nhau nhằm thể hiện được các khía cạnh của khái niệm đó. Trong luận văn này, chúng tôi chú trọng đến BDTQ, đặc biệt là các BDTQ với sự hỗ trợ của các phần mềm hình học động trên máy tính nhằm giúp HS phát triển năng lực suy luận.

1.1.2 Biểu diễn trực quan

Có nhiều quan điểm khác nhau về trực quan hóa. Với nội dung của luận văn này, tác giả luận văn sử dụng định nghĩa được tổng hợp bởi Arcavi (2003, [31], tr. 217) như sau:

Trực quan hóa là quá trình và sản phẩm của sự sáng tạo, giải thích, sử dụng và phản ánh dựa trên các hình vẽ (hay hình ảnh, sơ đồ...) trong đầu chúng ta, trên giấy hay trên các công cụ khoa học công nghệ. Trực quan hóa nhằm mục đích mô tả và giao tiếp thông tin, tư duy và phát triển các ý tưởng chưa biết trước đó để đi đến việc hiểu.

Ví dụ 1.1: Tìm tổng vô hạn của cấp số nhân

1 1 1  ...

4 42 43

HS có thể dùng biểu diễn đại số để tính

S 1 1

1  ... 1 ,

rồi tính giới hạn:

11

4 42 43 4n

lim Sn  lim

( )

4 1

n

n4

113

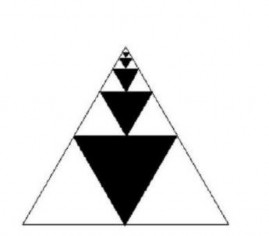
Một cách chứng minh khác (hình 1.2) của bài toán trên được trích từ bài báo mang tên “chứng minh không từ ngữ” của Mabry (xem Trần Vui, 2009, [29]) với việc sử dụng BDTQ như sau:

Giả sử diện tích tam giác đều lớn bằng 1. Từ tam giác đều lớn, ta đục tam giác đều ở giữa,

tiếp tục đục tam giác đều ở trên... Dãy tam giác đều bị đục có tổng diện tích là:

1 1 1  ...

Hình 1.2 BDTQ tổng vô hạn

4 42 43

Ta thấy có ba dãy tam giác đều vô hạn giống nhau và ba dãy này lấp đầy tam giác

đều lớn nên:

1 1 1  ... 1

4 42 43 3

học.

BDTQ là một công cụ hiệu quả cho việc học toán bởi:

+ BDTQ mang lại ý nghĩa cho các khái niệm toán học và các mối quan hệ toán

+ BDTQ cung cấp các tiếp cận đơn giản, ngắn gọn và đầy nội lực cho các kết quả

toán học, góp phần tạo ra sự kết nối giữa các lĩnh vực khác nhau của toán học như số

học, đại số và hình học.

+ BDTQ giúp gợi ý hướng giải quyết vấn đề.

+ BDTQ cung cấp thêm cho HS những công cụ và phương tiện, kĩ thuật khác nhau khi nhìn nhận một tình huống toán học.

1.1.3 Biểu diễn trực quan động

Khái niệm BDTQ động có thể hiểu là BDTQ trong đó cho phép sử dụng các thao tác tác động lên các đối tượng trong biểu diễn. BDTQ động thường được xây dựng thông qua các phần mềm hình học động trên máy tính. [24]

Phần mềm hình học động là các chương trình phần mềm máy tính được tạo ra để dựng các hình của bộ môn hình học. The Geometer Sketchpad (GSP), Cabri, Geogebra là ba trong số các phần mềm hình học động được sử dụng khá phổ biến trong giáo dục toán ở phổ thông hiện nay. Khía cạnh mang tính đột phá của những phần mềm này so với môi trường giấy bút truyền thống là tính “động”, nghĩa là các đối tượng trên BDTQ động có thể di chuyển nhưng vẫn bảo đảm giữ nguyên tính chất và các mối quan hệ hình học được thiết lập ban đầu.

Những thao tác lên BDTQ động trên máy tính khác cǜng sẽ khác với những thao tác lên các BDTQ trong môi trường giấy bút do chúng có thêm những hỗ trợ từ phần mềm hình học động mang lại.

Một số nhà nghiên cứu cho rằng, các phần mềm hình học động đã thay đổi cách suy nghĩ về các đối tượng hình học truyền thống vì trong khi di chuyển hay kéo rê các đối tượng hình học, đo đạc và kiểm tra các tính chất, người học có thể nhận ra các tính chất bất biến hình học [25]. Từ đó, giả thuyết ban đầu về các đối tượng hình học và

mối quan hệ giữa chúng được hình thành, sau đó, phần mềm hình học động cǜng hỗ

trợ quá trình kiểm tra tính đúng đắn của các giả thuyết đó [11].

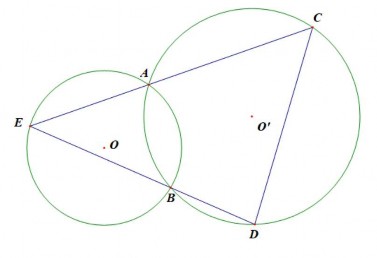
Ví dụ 1.2. Cho hai đường tròn (O) và (O’) cắt nhau tại A và B. Lấy điểm E trên (O) khác A, B. Đường thẳng EA và EB cắt (O’) lần lượt tại C và D. Tiến hành đo độ dài các đoạn thẳng EC, ED và CD.

Hình 1.3 Thao tác động cho điểm trên đường tròn

Khi bạn kéo điểm E quanh đường tròn (O), các độ dài EC và ED thay đổi nhưng độ dài CD là không đổi. Trong mô hình này có thể thấy đường tròn khi thay đổi vị trí của nó, thay đổi kích thước của đường tròn, dựng thêm các đối tượng khác… Rò ràng, việc chủ động phát hiện ra độ dài CD là không đổi có ý nghĩa hơn so với việc bạn được yêu cầu chứng minh nó. Việc giá trị CD không đổi gây cho bạn ngạc nhiên, thú vị và gợi động cơ chứng minh phát hiện này.

Những trải nghiệm nhờ các thao tác động trong ví dụ này hoàn toàn khác với những trải nghiệm khi thực hiện trong điều kiện chỉ có giấy và bút. Bạn sẽ không thấy được một cách trực quan những chuyển động, những biến đổi của các đối tượng. Chúng ta chỉ có thể dự đoán rồi làm việc với những biểu diễn ký hiệu để khẳng định chúng. Chúng ta cǜng có thể dự đoán được những ứng xử như trên của mô hình nhưng điều đó cǜng chỉ dừng lại ở mức độ dự đoán. Số hình ảnh thu được từ mắt mình chỉ là một, trong khi thao tác trên mô hình, bạn sẽ thu nhận được vô số những biến thể của hình đó.

Phần mềm hình học động có thể hỗ trợ hiệu quả cho việc học toán bằng các thao tác động, trong đó người học khám phá, thực nghiệm và hình thành kiến thức toán học thông qua các tương tác. Theo Finzer và Jackiw (1998, [49]), các môi trường thao tác động được đặc trưng bởi ba tính chất:

- Thao tác trực tiếp. Vẽ đồ thị hàm số f(x) rồi dựng một cát tuyến đi qua hai điểm E0 và E trên đồ thị. Bạn nắm lấy điểm E rồi kéo rê nó đến với điểm E0. Bạn sẽ nói “Tôi kéo rê điểm E” chứ không nói “Tôi kéo rê chấm tròn nhỏ này và nó sẽ làm thay đổi vị trí của điểm E”.

- Chuyển động cập nhật liên tục. Các thay đổi được cập nhật liên tục trong suốt quá trình kéo rê. Các đối tượng toán học có trên màn hình vẫn liên kết

trong một tổng thể tại mọi thời điểm. Chẳng hạn, nếu tính giá trị khoảng cách từ E tới E0 thì giá trị hiển thị trên màn hình này sẽ thay đổi tương ứng với vị trí của điểm E khi kéo rê.

- Môi trường thuận lợi cho các thao tác. Thực nghiệm của bạn chỉ liên quan đến những đối tượng mà bạn thao tác. Bạn khám phá khi làm việc với chúng. Giao diện của chương trình hầu như không gây ra tác động nào và bạn có thể tập trung làm thế nào để đạt được những mục đích toán học chứ không phải làm thế nào để điều khiển công nghệ.

Đối với việc học toán, các thao tác động có thể giải quyết được những vấn đề chẳng hạn như lý giải về sự liên tục. Thông qua chương trình học, học sinh học toán đối mặt với hai hiện tượng: liên tục và rời rạc. Tuy nhiên những công cụ mà giáo viên đưa ra để lý giải về các hiện tượng này chưa tạo ra cầu nối giữa chúng. Giáo viên thường mô tả chúng trên bảng, nhưng điều này chỉ đưa ra một trường hợp đặc biệt, trong đó học sinh thấy rằng một số điều kiện được nghiệm đúng và tất nhiên nó chưa thể hiện đầy đủ trường hợp tổng quát. Sau đó giáo viên thường đưa ra một biểu diễn liên hệ giữa các ký hiệu toán học để tổng quát tất cả các ví dụ liên quan. Nhưng chúng ta có thể tìm thấy được đầy đủ các trường hợp ở đâu trong biểu diễn mà nó chứa đựng?

Các phần mềm cho phép các thao tác động sẽ giúp chúng ta vượt qua thiếu sót này. Khi học sinh trực tiếp thay đổi một tham số, các em sẽ hiểu được việc tạo ra một

số tiến dần ra vô hạn của những trường hợp ví dụ liên quan đến tính liên tục. Hình ảnh lúc này không chỉ đơn thuần là minh họa nữa mà thông qua những thao tác động, nó giúp học sinh tiếp cận trường hợp tổng quát. Các thao tác động sẽ giúp người học biết được ứng xử của các đối tượng toán học. Chẳng hạn, xét hai mô tả sau của một tam giác cân:

- Hai cạnh bên của tam giác cân bằng nhau, hai góc đối diện tương ứng với hai cạnh đó bằng nhau.

- Dù bạn có biến đổi hình dạng của tam giác như thế nào đi nữa thì hai cạnh bên vẫn bằng nhau và hai góc tương ứng vẫn bằng nhau.

Mô tả ban đầu liệt kê hai tính chất của tam giác cân trong khi mô tả sau diễn tả ứng xử của nó. Cái đầu tiên mang tính tường thuật và ở trạng thái tĩnh, cái thứ hai có tính mệnh lệnh và cơ học. Sự khác nhau đó còn được nhấn mạnh ở chỗ một tam giác cân xác định đại diện cho tất cả các tam giác cân ở mô tả đầu trong khi đó một tam giác có thể trở thành tam giác cân nếu nó thỏa mãn mô tả sau. Trong những tình huống học tập và giải quyết vấn đề, khi một danh sách tĩnh của các tính chất chỉ thích hợp với việc tóm tắt thì mô hình thao tác động dẫn đến sự xác nhận và suy luận.

Biểu diễn trực quan động sẽ nằm ở phạm trù biểu diễn biểu tượng theo sự sắp xếp của Bruner (trong Tadao, 2007, [48]). Tuy nhiên những biểu diễn này ngoài việc mang tính minh họa trực quan, nó còn cho phép người khảo sát thực hiện những thao tác lên các đối tượng có trong biểu diễn. Những đối tượng này gắn kết với nhau một cách chặt chẽ trong mối quan hệ toán học đã được xác định trước. Việc thao tác lên một đối tượng nào đó trong biểu diễn nhiều lúc không chỉ nó bị tác động mà những đối tượng liên quan khác cǜng bị tác động theo. Chẳng hạn, khi bạn thay đổi biểu thức của một hàm số trong biểu diễn trực quan động, đồ thị của nó cǜng thay đổi theo dù bạn không hề tác động đến đồ thị.

Thông qua những kết quả nghiên cứu, hai tác giả Finzer và Jackiw (1998, [49]) đã đề xuất những vấn đề sau mà giáo viên cần tạo điều kiện và hỗ trợ học sinh trong việc học toán:

- Học sinh nên được thực nghiệm với những bài toán hoặc các tình huống trong

đó có sự biến đổi từ trạng thái này sang trạng thái khác để lý giải những trạng thái trung gian. Phần mềm thao tác động sẽ hỗ trợ học sinh thực nghiệm và khám phá những vấn đề này.

- Với một mô hình động đã cho, giáo viên cần tạo điều kiện để học sinh có thể phát hiện và diễn tả theo ngôn ngữ toán học những mối liên hệ tồn tại giữa các đối tượng có trên mô hình.

- Giáo viên cần tạo điều kiện cho học sinh thực nghiệm, trong đó các em sử dụng các công cụ toán học để xây dựng nên các mô hình thao tác được với cả những dụng cụ vật chất hoặc các công cụ trên máy tính.

- Ngoài việc liệt kê các thuộc tính của các đối tượng toán học, học sinh cần được sự động viên, khuyến khích của giáo viên trong việc suy nghĩ và diễn tả những ứng xử của các đối tượng đó.

- Giáo viên cần tạo nhiều cơ hội để học sinh khám phá toán học, khái quát hóa vấn đề và tham gia vào những khảo sát có kết thúc mở vì các phần mềm động cung cấp một môi trường chứa đựng nhiều thay đổi, tạo nên sự ngạc nhiên và bất ngờ.

Các biểu diễn toán trên máy tính có thể tạo ra những biến thể khác nhau của nó nhờ vào những thao tác của người dùng lên các đối tượng trong biểu diễn. Từ tưởng ban đầu là “hình học động”, các phần mềm hình học động đã có bước tiến lớn khi hỗ trợ người dùng xây dựng các đối tượng đại số, giải tích. Các dạng biểu diễn từ đó cǜng phong phú và đa dạng hơn, một kiến thức có thể được thể hiện dưới nhiều dạng biểu diễn khác nhau trên cùng một trang hình, có mối liên hệ toán học chặt chẽ với nhau.

1.1.4 Vai trò của biểu diễn trực quan

Các biểu diễn cung cấp cho học sinh những công cụ tư duy hiệu quả. Sử dụng biểu diễn trực quan như là một công cụ, học sinh có thể tiếp cận khái niệm cǜng như các ứng dụng của khái niệm. Biểu diễn ký hiệu giúp khẳng định những kết luận có được một cách chính xác, biểu diễn ngôn ngữ giúp cho việc chuyển và tiếp nhận thông tin.

Biểu diễn trực quan động cung cấp cho học sinh một môi trường học toán hiệu quả. Các biểu diễn trực quan động mô tả được các giai đoạn trung gian, giúp người

học thực hiện được những thao tác trên các đối tượng toán học, lưu giữ được những bất biến của đối tượng hình học, thực hiện được các tính toán một cách chính xác và tương ứng với những vị trí khác nhau của đối tượng.

Sự kết hợp hài hòa giữa các biểu diễn giúp giáo viên hỗ trợ tốt học sinh kiến tạo tri thức mới. Hầu hết các khái niệm và phương pháp được dạy trong chương trình đều xuất phát từ việc giải quyết các tình huống thực tế. Do đó, ban đầu giáo viên sử dụng biểu diễn thực tế rồi biểu diễn thao tác được, biểu diễn trực quan. Biểu diễn ngôn ngữ được sử dụng hầu hết trong quá trình thông tin giữa giáo viên – học sinh và học sinh – học sinh. Giờ học kết thúc với những ứng dụng của lý thuyết và việc hiểu được các biểu diễn ký hiệu.

Sử dụng các biểu diễn động giúp học sinh tiếp cận với bản chất của vấn đề trong hình học, từ đó đưa ra được cách giải quyết cho vấn đề. Nếu giáo viên cung cấp một môi trường học tập với biểu diễn trực quan động, học sinh có thể trải nghiệm với những biểu diễn khác nhau và chọn được các biểu diễn có ý nghĩa nhất. Những thông tin được lưu giữ trong trí óc về các biểu diễn có ý nghĩa này sẽ là những thành tố quan trọng trong hỗ trợ học sinh giải quyết vấn đề.

Công nghệ thông tin hỗ trợ tốt cho việc thiết kế các biểu diễn trực quan động. Công nghệ làm cho việc vẽ hình dễ dàng hơn, có thể tạo ra từ ba đến bốn loại biểu diễn thể hiện trên màn hình cùng một lúc. Các biểu diễn trực quan động với sự thể hiện đồng thời của hình học động, ký hiệu động và thể hiện số động là một thế mạnh rò ràng của việc ứng dụng công nghệ thông tin cho dạy học toán.

1.2. Năng lực và năng lực toán học

1.2.1. Năng lực

Khái niệm năng lực là một khái niệm thuộc phạm trù tâm lí học. Ngày nay, khái niệm năng lực được hiểu theo nhiều nghĩa khác nhau. Tuy nhiên, có thể kể đến một số quan niệm phổ biến về năng lực như sau:

Theo Tâm lý học, năng lực là tổ hợp các thuộc tính độc đáo của cá nhân, phù hợp với những yêu cầu của một hoạt động nhất định, đảm bảo cho hoạt động đó có kết quả [18].