Sử dụng biểu diễn trực quan phát triển năng lực suy luận toán học cho học sinh thông qua dạy học Hình học lớp 9

DANH MỤC HÌNH VẼ

Trang

Hình 1.1. Các giai đoạn phát triển có tính trình tự của biểu diễn 1

Hình 1.2 BDTQ tổng vô hạn. 3

Hình 1.3 Thao tác động cho điểm trên đường tròn 5

Hình 1.4. Dạng cơ bản của mô hình Toulmin 17

Hình 1.5. Mô hình Toulmin chứng minh ABC vuông 17

Hình 1.6. Mô hình Toulmin của một bước suy luận suy diễn 18

Có thể bạn quan tâm!

Xem toàn bộ 143 trang tài liệu này.

Hình 1.7. Mô hình Toulmin của một bước suy luận ngoại suy 19

Hình 1.8 Mô hình Toulmin của một suy luận quy nạp bằng KQH kết quả 19

Hình 1.9 Mô hình Toulmin của một suy luận quy nạp bằng khái quát hoá quá trình 19

Hình 1.10. 21

Hình 1.11 21

Hình 1.12 Cặp góc đối đỉnh tạo bởi các đường thẳng đồng quy 22

Hình 1.13 24

Hình 1.14 26

Hình 1.15 28

Hình 2.1 Sơ đồ chôn kho báu 41

Hình 2.2 42

Hình 2.3a. 42

Hình 2.3b. 42

Hình 2.4. 43

Hình 2.5. 44

Hình 2.6. 45

Hình 2.7. 45

Hình 2.8. 46

Hình 2.9. BDTQ minh họa ví dụ 2.4 48

Hình 2.10a 50

Hình 2.10b. 50

Hình 2.10c 50

Hình 2.11. 50

Hình 2.12. 52

Hình 2.13. 52

Hình 2.14. 54

Hình 2.15. 55

Hình 2.16. 56

Hình 2.17. 56

Hình 2.18a 57

Hình 2.18b. 57

Hình 2.18c 57

Hình 2.19. 59

Hình 2.20. 61

MỞ ĐẦU

1. Lý do chọn đề tài

1.1. Bối cảnh phát triển kinh tế quốc tế đặt ra những yêu cầu mới cho giáo dục. Ở Việt Nam, sự phát triển kinh tế - xã hội trong bối cảnh hội nhập quốc tế với những ảnh hưởng của xã hội tri thức và toàn cầu hóa tạo ra những cơ hội nhưng đồng thời đặt ra những yêu cầu mới đối với giáo dục trong việc đào tạo đội ngǜ lao động. Đào tạo nguồn nhân lực có trình độ cao đáp ứng nhu cầu phát triển kinh tế tri thức đang là thách thức không chỉ của ngành giáo dục mà còn là của toàn Đảng, toàn dân.

Nghị quyết số 29-NQ/TW ngày 04 tháng 11 năm 2013 của Hội nghị lần thứ 8 Ban chấp hành Trung ương Đảng khóa XI về đổi mới chương trình giáo dục phổ thông

[1] nhằm phát triển năng lực và phẩm chất, hài hòa đức, trí, thể, mỹ của HS. Tiếp tục đổi mới mạnh mẽ phương pháp dạy và học theo hướng hiện đại, vận dụng các phương pháp, kĩ thuật DH một cách linh hoạt, sáng tạo, hợp lý, phù hợp với nội dung, đối tượng và điều kiện cụ thể của cơ sở giáo dục phổ thông, phát huy tính tích cực, chủ động, sáng tạo của HS; thực hiện phương châm “giảng ít, học nhiều”, khắc phục lối truyền thụ áp đặt một chiều, ghi nhớ máy móc; tập trung dạy cách học, cách nghĩ, khuyến khích và rèn luyện năng lực tự học

Giáo dục định hướng phát triển năng lực được bàn đến từ những năm 90 của thế kỷ XX và ngày nay đã trở thành xu hướng giáo dục quốc tế. Năng lực không chỉ quan trọng đối với con người trong học tập mà còn trong thực tiễn đời sống.

Luật Giáo dục nước Cộng hòa xã hội chủ nghĩa Việt Nam năm 2019 đã quy định [21]: “Giáo dục phổ thông nhằm phát triển toàn diện cho người học về đạo đức, trí tuệ, thể chất, thẩm mỹ, kỹ năng cơ bản, phát triển năng lực cá nhân, tính năng động và sáng tạo; hình thành nhân cách con người Việt Nam xã hội chủ nghĩa và trách nhiệm công dân; chuẩn bị cho người học tiếp tục học chương trình giáo dục đại học, giáo dục nghề nghiệp hoặc tham gia lao động, xây dựng và bảo vệ Tổ quốc.”.

1.2. Mục tiêu đổi mới chương trình giáo dục phổ thông [9] là góp phần chuyển nền giáo dục nặng về truyền thụ kiến thức sang nền giáo dục phát triển toàn diện phẩm chất và năng lực của người học. Để thực hiện các mục tiêu này, Bộ Giáo dục và Đào

tạo đã phát động phong trào đổi mới giáo dục, nhấn mạnh vào đổi mới phương pháp dạy học trong toàn quốc. Cụ thể là tập trung vào đổi mới nội dung và các phương pháp giáo dục như phương pháp dạy học phân hóa, dạy học tích hợp, dạy học thông qua hoạt động tích cực của người học.

1.3. Toán học được coi như là một môn khoa học chứng minh. Tuy nhiên đó mới chỉ là một khía cạnh của nó. Bạn cần dự đoán một định lí toán học trước khi chứng minh nó. Hội đồng giáo viên toán quốc gia của Mỹ (NCTM, [30]) xác định: suy luận - chứng minh là một trong số mười tiêu chuẩn cho toán học nhà trường. NCTM [30] cho rằng khả năng suy luận là bản chất của việc hiểu toán và đó nên là mục tiêu đầu tiên của giáo dục toán: “Bằng việc phát triển các ý tưởng, khám phá các hiện tượng, xác minh các kết quả và sử dụng suy luận toán học trong tất cả các lĩnh vực, ở tất cả các lớp học, HS có thể nhìn thấy và tin tưởng rằng toán học là có ý nghĩa...”. NCTM [30] cǜng khẳng định: “Khả năng suy luận phát triển khi HS được cổ vǜ để đưa ra các dự đoán, được cho thời gian tìm kiếm các bằng chứng nhằm ủng hộ hay bác bỏ chúng, được mong chờ việc giải thích các ý tưởng... Nếu khả năng suy luận không được phát triển cho HS thì toán học chỉ là một tập hợp các công thức, thuật toán, quy tắc và các ví dụ mang tính biểu diễn mà không hiểu tại sao chúng có ý nghĩa.”

1.4 Suy luận và biểu diễn là hai trong số tám năng lực được chọn để đánh giá trong Chương trình đánh giá học sinh quốc tế PISA, một chương trình do Tổ chức hợp tác và phát triển kinh tế OECD khởi xướng và chỉ đạo, nhằm tìm kiếm các chỉ số đánh giá tính hiệu quả, chất lượng của hệ thống giáo dục của mỗi nước tham gia, qua đó rút ra các bài học về chính sách đối với giáo dục phổ thông. Biểu diễn trực quan (BDTQ), một dạng của biểu diễn toán, không chỉ đóng vai trò minh họa cho các kết quả bằng biểu diễn kí hiệu mà còn được thừa nhận là một công cụ mạnh để khám phá các vấn đề toán học (Arcavi, 2003, [31]). Biểu diễn trực quan cho phép HS trao đổi các cách tiếp cận bài toán, các suy luận và việc hiểu của HS, giúp HS nhận thấy ý nghĩa của các khái niệm toán học và mối quan hệ giữa chúng. Để từ đó áp dụng vào suy luận toán cho những vấn đề thực tế (NCTM, 2000, [30]).

Mặt khác, thực tiễn giảng dạy bộ môn Toán 9 hiện nay ở trường Trung học cơ

sở còn nhiều bất cập trong phương pháp giảng dạy, truyền thụ tri thức cho học sinh.

Đặc biệt đối với hình học 9, HS vẫn còn gặp nhiều khó khăn trong việc tiếp cận các bài toán vì chưa thể quan sát, hình dung một cách trực quan các kiến thức. HS chưa biết sử dụng các công cụ trực quan để suy luận tìm ra lời giải các bài toán.

Chính vì vậy đòi hỏi giáo viên cần có biện pháp để thể hiện kiến thức được trực quan, dễ hiểu và dễ hình dung nhất nhằm giúp HS phát triển năng lực suy luận. Hiện nay, các nghiên cứu theo hướng này phát triển mạnh mẽ, được nhiều người quan tâm.

Với những lí do trên, tôi lựa chọn đề tài nghiên cứu: “Sử dụng biểu diễn trực quan phát triển năng lực suy luận toán học cho học sinh thông qua dạy học hình học lớp 9”.

2. Mục đích nghiên cứu

Trên cơ sở nghiên cứu về việc phát triển năng lực suy luận ở trường THCS đề xuất một số biện pháp sư phạm sử dụng biểu diễn trực quan nhằm phát triển năng lực suy luận cho học sinh trong dạy học môn Toán ở trường THCS.

3. Khách thể, đối tượng và phạm vi nghiên cứu

3.1. Khách thể nghiên cứu: Quá trình dạy học ở trường THCS.

3.2. Đối tượng nghiên cứu: Nghiên cứu những năng lực thành phần của năng lực suy luận toán học và biện pháp sử dụng biểu diễn trực quan để phát triển năng lực suy luận cho HS THCS thông qua dạy học Hình học 9.

3.3. Phạm vi nghiên cứu: HS ở trường THCS.

4. Giả thuyết khoa học

Dựa trên cơ sở lí luận và thực tiễn, xác định được các vấn đề trong dạy học hình học lớp 9 và đề xuất được một số biện pháp sử dụng biểu diễn trực quan thích hợp để có thể phát triển năng lực suy luận cho HS ở trường THCS góp phần nâng cao chất lượng dạy và học môn Toán ở trường THCS.

5. Nhiệm vụ nghiên cứu

5.1. Nghiên cứu các quan điểm mang tính lí luận về năng lực suy luận toán học.

5.2. Đề xuất một số biện pháp sư phạm nhằm phát triển năng lực suy luận cho học sinh trong dạy học hình học lớp 9 bằng sử dụng biểu diễn trực quan.

5.3. Thực nghiệm sư phạm để kiểm chứng và đánh giá tính khả thi của giả thuyết khoa học và các câu hỏi nghiên cứu.

Các câu hỏi nghiên cứu cụ thể là:

1. Tại sao cần phải phát triển năng lực suy luận cho HS ở trường THCS? Những năng

lực thành phần của suy luận là gì?

2. Thực trạng của việc dạy học hình học 9 ở các trường THCS như thế nào?

3. Đề xuất các biện pháp để phát triển năng lực suy luận cho HS.

4. Sử dụng biểu diễn trực quan động như thế nào để hỗ trợ quá trình suy luận khi khám phá quy luật trong các bài toán hình học.

6. Phương pháp nghiên cứu

6.1. Phương pháp nghiên cứu lý luận: Tìm hiểu, nghiên cứu tài liệu về các vấn đề liên quan đến đề tài của luận văn.

6.2. Phương pháp điều tra - quan sát: Nghiên cứu thực trạng dạy và học nội dung toán học tại một số trường THCS thông qua các hình thức sử dụng phiếu điều tra, quan sát hoặc phỏng vấn trực tiếp GV ở trường THCS.

6.3. Thực nghiệm sư phạm: Tổ chức dạy thực nghiệm tại một số trường THCS để xem

xét tính khả thi và hiệu quả của các biện pháp sư phạm đã đề xuất.

7. Đóng góp của luận văn

7.1. Những đóng góp về mặt lý luận

Đề xuất được một số biện pháp sư phạm mang tính khả thi nhằm phát triển năng

lực suy luận toán học cho học sinh lớp 9.

7.2. Những đóng góp về mặt thực tiễn

- Nâng cao hiệu quả dạy và học ở trường THCS.

- Kết quả luận văn có thể sử dụng làm tài liệu tham khảo cho giáo viên và HS trong quá trình giảng dạy và học tập ở trường THCS.

- Làm cơ sở để phát triển những nghiên cứu sâu, rộng hơn về những vấn đề có liên quan trong luận văn.

8. Cấu trúc của luận văn

Ngoài phần “Mở đầu”, “Kết luận” và “Danh mục tài liệu tham khảo”, nội dung

chính của luận văn được trình bày trong ba chương: Chương 1: Cở sở lý luận và thực tiễn.

Chương 2: Mội số biện pháp sư phạm sử dụng biểu diễn trực quan để phát triển năng

lực suy luận toán học cho học sinh.

Chương 3: Thực nghiệm sư phạm

Chương 1

CƠ SỞ LÍ LUẬN VÀ THỰC TIỄN

1.1 Biểu diễn toán học

1.1.1 Phân loại biểu diễn toán học

Theo Từ điển từ và ngữ Việt Nam, biểu diễn là: “ghi bằng hình vẽ hoặc kí hiệu”

[18, tr.147]

Có nhiều định nghĩa khác nhau về biểu diễn (representation) trong giáo dục toán. Hầu hết các nhà nghiên cứu giáo dục toán phân biệt giữa biểu diễn trong (internal representation) và ngoài (external), trong đó biểu diễn ngoài là những biểu hiện của các ý tưởng hoặc khái niệm như biểu đồ, bảng biểu, đồ thị, sơ đồ, ngôn ngữ… và biểu diễn trong là các mô hình nhận thức mà một người có được trong trí óc họ.

Tác giả Asli (1998, [32]) đã đề xuất vai trò của các biểu diễn toán trong dạy học như sau:

 Các biểu diễn là một phần không tách rời của toán học;

 Các biểu diễn là những cụ thể hóa khác nhau của một khái niệm nào đó;

 Các biểu diễn được sử dụng để giảm bớt độ khó của vấn đề;

 Các biểu diễn nhằm làm cho toán học hấp dẫn và thú vị hơn.

Bruner, nhà tâm lý học nhận thức người Mỹ đã mô tả các giai đoạn phát triển của biểu diễn theo trình tự từ biểu diễn thực tế đến biểu diễn ký hiệu như sau (Tadao Nakahara, 2007, [48]):

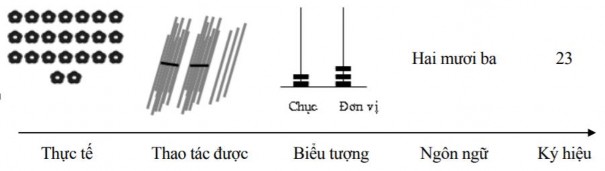
Hình 1.1. Các giai đoạn phát triển có tính trình tự của biểu diễn