Phát triển tư duy biện chứng của học sinh trong dạy học Hình học ở trường trung học phổ thông

- SGK không thể trình bày một cách đầy đủ và chính xác các vấn đề được nêu ra, bởi vì đây là sách dùng cho HS chứ không phải là sách để nghiên cứu. Tuy nhiên, với phương châm "biết mười dạy một", các GV rất cần nắm được thực chất KH của các vấn đề mà mình sẽ giảng dạy. Chẳng hạn, nếu không chuẩn bị trước, một GV nào dó có thể lúng túng khi phải trả lời cho HS cách viết đường phân giác trong tại một đỉnh của tam giác đã cho.

- Theo tinh thần của chương trình, sau khi học xong lớp 12, HS sẽ hiểu được các kiến thức cơ bản về HH phẳng và HH KG, đồng thời nắm được 2 PP chủ yếu để nghiên cứu HH là PP tổng hợp và PPTĐ.

- Khi nói đến PPTĐ là nói đến PP xác định vị trí của một điểm trong mp hay trong KG, từ đó xác định được vị trí và tính chất của một tập hợp điểm là một đường trong mp hay là một đường hoặc một mặt trong KG. SGK chỉ trình bày các đường và mặt đơn giản nhất để HS hiểu được ý nghĩa của PPTĐ. GV không nên đi sâu vào khái niệm đường và phương trình của đường trong mp Oxy vì đó là một khái niệm khó trình bày chính xác. Chỉ nên nêu các VD như trong SGK. Các kiến thức HH đã học ở các lớp dưới hỗ trợ đắc lực cho việc học HH ở Lớp 12.

Chẳng hạn, khi cần tìm phương trình của các tiếp tuyến chung của hai đường tròn, trước hết ta cần biết vị trí tương đối của hai đường tròn ấy. Nếu hai đường tròn ấy ở ngoài nhau tức là khoảng cách giữa hai tâm lớn hơn tổng của hai bán kính thì hai đường tròn ấy có 4 tiếp tuyến chung.

Với những BT có yêu cầu vẽ hình thì HS cần vẽ hình càng chính xác càng tốt. Với các BT khác thì không yêu cầu HS vẽ hình chính xác nhưng nên tập cho HS vẽ hình tương đối đúng để từ đó tìm ra phương hướng giải và kiểm nghiệm lại lời giải, tuy nhiên không chấp nhận lời giải và đáp số do hình vẽ mang lại mà không có suy luận.

HS cần nắm được cách giải quyết các vấn đề cơ bản của HH phẳng bằng PPTĐ, biết cách lập phương trình của đường thẳng, đường tròn, elip, hypebol, parabol và rút ra các tính chất HH của các đường đó từ các phương trình của chúng ở HH 10.

Yêu cầu, mức độ: HS hiểu được sự phát triển lôgic của mạch kiến thức từ định lí về điều kiện cần và đủ để hai vectơ cùng phương đến kết luận về việc phân tích 1

vectơ theo 2 vectơ khác không cùng phương. HS nắm vững định nghĩa các khái niệm: HTĐ Đêcac vuông góc, tọa độ của một điểm, mp tọa độ, tọa độ vectơ, ...

Về kĩ năng: yêu cầu HS thành thạo trong việc phân tích một vectơ theo hai vectơ cho trước, xác định tọa độ của vectơ biết tọa độ của điểm ngọn, gốc của véctơ ấy, xác định tọa độ của vectơ tổng, hiệu, tích của vectơ với số, ... HS hiểu thêm ý nghĩa thực tế của việc học vectơ. Ở trường PT chỉ xét HTĐ vuông góc với các vectơ đơn vị của hai trục bằng nhau.

Theo Văn Như Cương, sách GV cũng là một công cụ đắc lực giúp GV giảng dạy tốt vì nó thoả mãn: Làm cho GV hiểu rõ hơn và hiểu sâu hơn các vấn đề giảng dạy theo SGK, bằng cách cung cấp những thông tin, những sự giải thích và những kiến thức cần thiết xung quanh những vấn đề ấy, nhằm góp phần nâng cao trình độ chuyên môn cho GV. Giới thiệu cho GV những PP sư phạm tương đối mới trong việc giảng dạy lí thuyết và hướng dẫn giải bài tập, nhằm góp phần nâng cao nghiệp vụ sư phạm cho GV. Phổ biến cho GV những kinh nghiệm tốt trong việc xử lí những tình huống HS dễ mắc sai lầm khi tiếp thu bài học mới hoặc giải bài tập khó, nhằm góp phần nâng cao tác dụng GD của GV.

- Giải BT bằng PPTĐ

Với nhiều BT HH có chứa yếu tố "khoảng cách", "cùng phương" và đặc biệt là yếu tố "vuông góc", nếu khéo chọn HTĐ thì có thể chuyển được thành BT ĐS có nhiều hứa hẹn cho khả năng tìm ra lời giải. Đó là tư tưởng sử dụng PPTĐ để giải toán.

+ Tọa độ: Khi nghiên cứu HH phẳng và HH KG ở chương trình toán ở trường PT bằng PPTĐ, chúng ta đã dùng các số thực và các phép toán của trường số thực. Đây là một quá trình trừu tượng hoá và khái quát hoá trong việc rèn luyện TD Toán học.

+ Các bước giải một BT bằng PPTĐ

* Chọn HTĐ thích hợp đó là HTĐ được gắn với nhiều yếu tố của BT.

* Biểu thị các dữ kiện đã cho, cần tìm của BT theo toạ độ.

* Giải bằng PP đại số các biểu thức toạ độ để rút ra kết luận. Chuyển các kết quả tính toán được bằng công cụ đại số sang các tính chất HH cần chứng minh hay cần tính toán.

Chẳng hạn (đề thi tuyển sinh ĐH khối A năm 2002): Cho hình chóp tam giác đều S.ABC đỉnh S, có độ dài cạnh đáy bằng a. Gọi M và N lần lượt là trung điểm của các cạnh SB và SC.

Tính theo a diện tích AMN biết rằng mp(AMN) mp(SBC).

N I

A H K

Ngoài hai PP như trong đáp án của Bộ và cách đề xuất của Nguyễn Anh Dũng trên Tạp chí Toán học tuổi trẻ, số 7

tháng 8/2002 ta có cách giải bằng PPTĐ đơn giản như sau:

C Chọn hệ tọa độ Đêcac vuông góc Oxyz sao cho: K(0;0;0), B(a/2 ; 0; 0), C( a/2; 0; 0),

B a 3,

a 3

trong đó h là độ dài đường cao

Hình 2.6

A0;

2

;0



S0;

6

; h 



SH của hình chóp SABC. Từ đó suy ra kết quả.

(Tương tự khối B, D nếu ta sử dụng PPTĐ thì việc giải các BTHH rất đơn giản).

Trong câu 3 ý 1 đề thi tuyển sinh môn Toán năm 2003, khối A nếu sử dụng PPTĐ thì việc giải cũng sẽ đơn giản hơn nhiều, không phức tạp theo cách dùng PP tổng hợp như trong hai cách giải của đáp án.

Như vậy, để vận dụng tốt PPTĐ, một trong các vấn đề lưu ý quan tâm đó là sự chuyển đổi tương đương giữa ngôn ngữ HH tổng hợp và ngôn ngữ tọa độ của các yếu tố HH.

VD 3: Cho một hình hộp chữ nhật đường chéo tạo với ba cạnh xuất phát từ một đỉnh ba góc , , . Chứng minh rằng: cos 2 + cos2 + cos2 = 1.

Giải: Cách 1 (PP tọa độ): Ở đây ta chứng minh với BD là đường chéo, các đường chéo khác khác hoàn toàn tương tự.

Chẳng hạn, lấy đường chéo BD1 và ba cạnh xuất phát từ đỉnh A1.

Chọn hệ trục tọa độ Oxyz sao cho O  A1, D1 thuộc tia Ox, B1 thuộc tia Oy, A

thuộc tia Oz.

Gọi D1(a, 0, 0); B1(0, b, 0);

A(0, 0, c); B(0, b, c)

Khi đó: A D (a,0,0); A B (0, b,0); A A(0,0, c); BD (a,b,c);

1 1 1 1 1 1

Hình 2.7

ta có:

cos

cos( A1 D1 , BD1 ) 

a  cos

a 2 b2 c 2

a 2 b 2 c 2

b

2 

a 2

a 2 b2 c 2 .

b 2

cos cos( A1 B1 , BD1 ) 

 cos

a b 2

c 2 .

cos cos( A A1 , BD1 ) 

c  cos 2 

c 2



a 2 b2

c 2 .

a 2 b 2 c 2

Suy ra: cos2 + cos2 + cos2  = 1.

Cách 2 (PP tổng hợp)

Lấy đường chéo AC1 và ba cạnh xuất phát từ đỉnh A.

Đặt:  = BAC1,  = DAC1,  = A1 AC1; AB = a, AD = b, AA1 = c.

Vì AB  (BCC 1B1)  AB  BC1. Suy ra tam giác ABC = 1 vuông tại B, ta có:

2 2 2 2 2 2 2 2 2

AC1 AB BC1 AB AD AA 1 a b c . B C

hay

AC1 

a 2 b 2 c 2 ; cos

AB a . A

a 2 b 2 c 2

AC1

Tương tự:

cos b; cos

c.

a 2b 2c 2

Hình 2.8

 cos2 + cos2 + cos2  = 1.

VD 4: Sự tự vận động và phát triển đi đến sự hoàn chỉnh của giá trị lượng giác (tỉ số lượng giác) của một góc bất kì.

- Giá trị lượng giác của góc nhọn [21, tr. 72].

Cho góc nhọn . Vẽ một tam giác vuông có một góc nhọn . Ta có thể vẽ như sau: Vẽ góc , từ một điểm bất kì B trên một cạnh của góc kẻ đường vuông góc với cạnh kia, xác định cạnh đối và cạnh kề của góc .

B’

Nhận xét mở đầu:

Nêu được tính chất cơ bản: Các tỉ số lượng giác của góc nhọn không phụ thuộc vào vị trí điểm B mà phụ thuộc vào độ lớn của góc.

Hình 2.9

A’ x

Chẳng hạn, lấy điểm bất kì B’ B trên Cy thì ta có:

CA CA' , BA B' A' ,

BA B' A' .

CB CB' CB

CB' CA CA'

Định nghĩa

Tỉ số giữa cạnh đối và cạnh huyền

được gọi là sin của góc , kí hiệu sin ;

Tỉ số giữa cạnh kề và cạnh huyền

được gọi là côsin của góc , kí hiệu cos ;

cạnh huyền

cạnh kề

Hình 2.10

ạnh đối

Tỉ số giữa cạnh đối và cạnh kề được gọi là tang của góc , kí hiệu tg (hay tan );

Tỉ số giữa cạnh kề và cạnh đối được gọi là côtang của góc , kí hiệu cotg (hay cot ).

Như vậy; sin =

AB ; cos = AC ; tan = AB ; cot = AC .

BC BC AC AB

Hạn chế: Các tỉ số lượng giác của góc nhọn được định nghĩa trong tam giác vuông, dựa vào góc Hình học, đơn vị đo là độ, trong phạm vi góc:

00 < < 900 và 0 < sin < 1, 0 < cos < 1.

- Giá trị lượng giác của một góc bất kì [126, tr. 40].

Định nghĩa: Với mỗi góc (00 1800), ta xác định điểm M trên nửa đường tròn đơn vị sao cho: MOx = .

Giả sử điểm M có tọa độ (x; y). Khi đó,

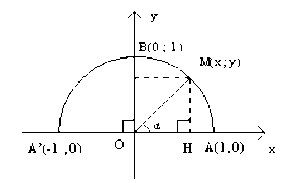
Hình 2.11

Tung độ y của điểm M gọi là sin của góc , kí hiệu là sin ; Hoành độ x của điểm M gọi là côsin của góc , kí hiệu là cos ;

Tỉ số

y (với x  0) gọi là tang của góc , kí hiệu là tan ;

Tỉ số

x (với y  0) gọi là côtang của góc , kí hiệu là cot .

Như vậy: Các số sin , cos , tan , cot gọi là các giá trị lượng giác của góc .

Khi đó: sin = y; cos = x; tan

 sin

cos

= y ; cot

 cos= x .

siny

Các tỉ số lượng giác của góc bất kì được định nghĩa trên nửa đường tròn đơn vị, trong hệ tọa độ Oxy, dựa vào góc HH, đơn vị đo là độ, trong phạm vi góc (00 1800) và 1 cos 1, 0 sin 1.

Sự phát triển

- Định nghĩa trong tam giác vuông phát triển thành định nghĩa trên nửa đường tròn đơn vị trong hệ tọa độ Oxy.

- Phạm vi góc được mở rộng từ 00 < < 900 thành 00 1800.

- Giá trị của sin và cos được mở rộng:

0 < sin < 1 thành 0 sin 1; 0< cos < 1 thành 1 cos 1.

Hạn chế

- Dựa vào góc HH chưa phù hợp với góc quay trong thực tế.

- Đơn vị đo là độ chưa thể hiện tính thống nhất với định nghĩa hàm số mà Đại số 10 đưa ra.

- Phạm vi góc trong giới hạn 00 1800.

- Giá trị của sin: 0 sin 1.

- Định nghĩa mới chỉ trên nửa đường tròn đơn vị.

- Các hàm số lượng giác [126, tr. 12].

Khái niệm các hàm số lượng giác là sự phát triển đi tới hoàn chỉnh của khái niệm tỉ số lượng giác của một góc bất kì.

- Các giá trị lượng giác của cung :

Với mỗi số thực , cung lượng giác có số đo được biểu diễn bởi một điểm M trên đường tròn lượng giác sao cho sđ AM = .

Định nghĩa: Tung độ y của điểm M gọi là sin của và kí hiệu là sin : sin = y;

Hoành độ x của điểm M gọi là côsin của

và kí hiệu là cos : cos = x; y B 1

tan =

cot =

sin 

cos

cossin 

(cos  0);

(sin  0).

M y

A’ A

-1 x O 1 x

- Các hàm số lượng giác của biến số thực:

Hàm số sin:

sin: R R

x a y = sinx.

B’ -1

Hình 2.12

Hàm số côsin:

cos: R R

x a y = cosx.

Hàm số tan:

Gọi D1 = {xR / x 

k, k Z}. Ta có:

tan: D1 R

x a y = tanx.

Hàm số cot:

Gọi D2 = {xR / x 

cot: D2 R

k, k Z}. Ta có:

x a y = cotx.

Các giá trị lượng giác của cung được định nghĩa trên đường tròn lượng giác trong hệ tọa độ Oxy, dựa vào góc (cung) lượng giác, đơn vị đo là radian, phạm vi góc bất kì và: 1 sin 1, 1 cos 1.

Sự phát triển: Định nghĩa trên nửa đường tròn đơn vị thành định nghĩa trên đường tròn lượng giác.

Từ góc HH thành góc (cung) lượng giác.

Phạm vi góc từ 00 1800 thành góc bất kì, kể cả góc âm. Đơn vị đo từ độ sang radian.

Giá trị của sin được mở rộng: 0 sin 1 thành 1 sin 1.

Nhu cầu của sự phát triển

- Nhu cầu thực tiễn

Từ định nghĩa góc Hình học thích hợp trong HH dẫn đến định nghĩa góc lượng giác phù hợp với thực tế: Góc quay.

- Nhu cầu KH

Đối số của hàm số lượng giác là số thực như các hàm số khác, thể hiện tính thống nhất.

Dùng số đo radian để thuận tiện cho việc nghiên cứu lí thuyết, làm cho các công thức tính toán đơn giản hơn.

Chẳng hạn:

Đơn vị đo là độ

Đơn vị đo là radian



/6 Bảng 2.



1 /4

