Biện Pháp 2 : Làm Cho Học Sinh Biết Xem Xét Các Đối Tượng Toán Học Dưới Nhiều Khía Cạnh Khác Nhau Và Xem Xét Đối Tượng Toán Học Trong Mối Liên Hệ

Đoạn thẳng AB và vectơ AB là hoàn toàn khác nhau. Bởi vì vectơ AB chính là

đoạn thẳng AB đã được định hướng (hướng từ điểm A đến điểm B).

Hai vectơ AB và BA không phải là một, mà là hai vectơ khác nhau. Vậy ứng với mỗi đoạn thẳng thì ta sẽ có hai vectơ khác nhau.

+ Với trường hợp A trùng B thì ta có vectơ AA hay BB , gọi là vectơ  không (kí hiệu là O ).

Vậy ứng với một điểm thì ta có một vectơ  không và mọi vectơ  không đều như nhau.

VD 4: Khái niệm hai vectơ cùng phương, cùng hướng [126, tr. 5].

Định nghĩa: Hai vectơ được gọi là cùng phương nếu chúng có giá song song hoặc trùng nhau.

Khi dạy định nghĩa này cần làm cho HS hiểu được “Khái niệm giá của vectơ”: Với mỗi vectơ AB (khác O ), đường thẳng AB được gọi là giá của vectơ AB .

Có thể bạn quan tâm!

• Rèn Và Phát Triển Tư Duy Biện Chứng Cần Chú Trọng Tới Việc Rèn Luyện, Bồi Dưỡng Cách Thức Tìm Tòi Và Vận Dụng Kiến Thức Của Từng Lĩnh Vực Toán
• Phát triển tư duy biện chứng của học sinh trong dạy học Hình học ở trường trung học phổ thông - 13
• Phát triển tư duy biện chứng của học sinh trong dạy học Hình học ở trường trung học phổ thông - 14
• Phát triển tư duy biện chứng của học sinh trong dạy học Hình học ở trường trung học phổ thông - 16
• Phát triển tư duy biện chứng của học sinh trong dạy học Hình học ở trường trung học phổ thông - 17
• Phát triển tư duy biện chứng của học sinh trong dạy học Hình học ở trường trung học phổ thông - 18

Xem toàn bộ 225 trang tài liệu này.

Còn với vectơ  không AA thì mọi đường thẳng đi qua A đều gọi là giá của nó.

- Cơ sở: Khái niệm hai vectơ cùng phương có cơ sở KH từ khái niệm hai đường thẳng cùng phương. Thực tế thì không phải các đại lượng có hướng luôn có hướng như nhau, mà có sự phân biệt phương, hướng giữa chúng, nên từ dó có khái niệm phương, hướng của hai vectơ.

Q

P

N

B M

E

A

F

D

C

Các vectơ cùng phương Các vectơ không cùng phương

Hình 2.20

Bản chất:

+ Hai vectơ AB , CD cùng phương (giá song song với nhau) là cùng hướng nếu chúng

thuộc nửa mặt phẳng bờ là đường thẳng đi qua hai đầu mút A, C.

+ Hai vectơ AB , EF cùng phương (có giá song song với nhau) là ngược hướng nếu

chúng thuộc hai nửa mặt phẳng đối nhau bờ là đường thẳng đi qua hai đầu mút A, E.

A

E

A B

c B

C D

F

Hình 2.21

+ Hai vectơ CD , EF cùng phương (có giá trùng nhau) nhưng ngược hướng (chúng không cùng hướng) vì vectơ CD hướng lên phía trên, còn vectơ EF hướng xuống dưới.

+ Vectơ  không cùng phương, cùng hướng với mọi vectơ.

VD 5: Khái niệm tổng của hai vectơ [126, tr. 10].

Định nghĩa: Cho hai vectơ a và b . Lấy một điểm A nào đó rồi xác định các điểm B và C sao cho AB = a , BC = b . Khi đó vectơ AC được gọi là tổng của hai vectơ a và b . Kí hiệu: AC = a + b .

Phép lấy tổng của hai vectơ được gọi là phép cộng vectơ.

B

a

b

a + b

a

b C

A

Hình 2.22

Khi dạy khái niệm này, GV cần làm cho HS biết

- Nguồn gốc của khái niệm: Trong thực tế có những vật cùng một lúc chịu nhiều lực tác dụng lên nó. VD như: Một vật treo bằng dây trên xà ngang, vật chịu tác dụng của trọng lực P và lực căng sợi dây F ; hay một con thuyền neo tại bến bởi một dây

neo, chịu tác dụng của lực đẩy dòng nước

F1 , sức gió thổi

F 2 và sức căng dây neo

F 3 … Vấn đề đặt ra: Hợp của tất cả các lực tác dụng lên vật treo trên xà ngang, lên

con thuyền là bao nhiêu? Từ đó, tổng của hai vectơ ra đời.

- Bản chất đối tượng: Phép cộng hai vectơ được định nghĩa không phụ thuộc vào điểm A ban đầu.

Nếu ta chọn điểm

A1 A , thì ta cũng sẽ được:

A1 B1 = a ,

B1C1 = b và

B

A1C1 = a + b = AC .

a

b

a + b

B1

a

b

a + b

C1

A

C

1

A Hình 2.23

2.5.2. Biện pháp 2: Làm cho học sinh biết xem xét các đối tượng Toán học dưới nhiều khía cạnh khác nhau và xem xét đối tượng Toán học trong mối liên hệ với các đối tượng Toán học có liên quan

a. Làm cho học sinh biết xem xét các đối tượng Toán học dưới nhiều khía cạnh khác nhau

- TDBC ở đây là làm cho HS cảm nhận được quy luật "toàn diện" của lôgic BC. Khi xem xét sự vật phải xem xét một cách đầy đủ, trong tất cả các mặt, các mối quan hệ (bên trong và bên ngoài, trực tiếp và gián tiếp) trong tổng thể những mối quan hệ phong phú, phức tạp và muôn vẻ của nó với các sự vật khác. Giúp HS tránh được những sai lầm xem xét chủ quan, phiến diện.

- Khi DH toán cần giúp HS học toán một cách sáng tạo, tìm được nhiều lời giải khác nhau cho một BT, tìm được PP giải độc đáo, còn giải theo cách thông thường thì khó khăn nhiều hơn, có khi bế tắc.

VD 1: Khi dạy định lí hàm số côsin ở SGK HH lớp 10 thể hiện bởi 3 công thức: a2 = b2 + c2 2bc.cosA (1)

b2 = a2 + c2 2ac.cosB (2)

c2 = a2 + b2 2ab.cosC (3)

Khi dạy công thức này cần khai thác các cách thể hiện khác nhau của công thức ta phải tập cho HS xem xét đối tượng dưới nhiều khía cạnh khác nhau, có cái nhìn sinh động từ nhiều phía đối với các sự vật và hiện tượng chứ không phải cái nhìn bất biến phiến diện, cứng nhắc và các cách thể hiện khác nhau của một công thức giúp cho chúng ta vận dụng sáng tạo định lí vào việc giải các BT khác nhau.

Chẳng hạn, công thức (1) có thể viết lại theo các cách sau:

a2 = (b + c)2 4bc.cos2(A/2) (1')

a2 = (b c)2 4bc.sin2(A/2) (2')

a2 = b2 + c2 4S.cotA (3') Nhờ các cách viết đó mà gợi ý cho chúng ta cách giải các BT sau:

BT 1: Trong các tam giác ABC có Â =  không đổi và tổng hai cạnh bên b + c = m không đổi. Tìm tam giác có chu vi bé nhất và diện tích lớn nhất.

Đối với BT này ta áp dụng cách viết (1') để giải:

Giải: Áp dụng (1') ta có: a2 = (b + c)2 4bc.cos2(A/2)

Do b + c = m không đổi nên chu vi tam giác nhỏ nhất  a nhỏ nhất  a2 nhỏ

nhất  4bc.cos2(A/2) lớn nhất  bc lớn nhất (Â không đổi)  b = c = diện tích tam giác ABC cũng lớn nhất.

m. Khi này

2

Vậy trong các tam giác ABC có Â =  không đổi và tổng hai cạnh bên b + c = m không đổi thì tam giác cân tại A có chu vi bé nhất và diện tích lớn nhất.

BT 2: Trong tam giác ABC chứng minh rằng sin Aa.

2 2 bc

BT này nếu chúng ta sử dụng công thức (2') thì có được một lời giải ngắn gọn.

Giải: Theo (2'), ta có: sin2 A

2

a 2 - (b - c)2

=

4bc

a 2

4bc

 sin A 

2

a . Dấu "=" xảy ra  b = c ABC cân tại A.

2 bc

BT 3: Cho tam giác ABC có các góc A, B, C và 3 cạnh tương ứng là a, b, c; R là bán kính đường tròn ngoại tiếp của tam giác.

a 2 b 2 c2

CMR: cotA + cotB + cotC =

.R

abc

Đối với BT này chúng ta sử dụng cách viết (3') để giải.

Giải: Ta có: a2

= b2

+ c2

4S.cotA  cotA =

b 2 c2 - a 2

4S

Tương tự, ta cũng chứng minh được: cotB =

cotC =

a 2 b 2 c2

Do đó: cotA + cotB + cotC =

4S

a 2 c2 - b 2

4S

a 2 b 2 - c2

4S

a 2 b 2 c2

= .R

abc

VD 2: Giải phương trình: 3 .sinx + cosx = 2 (1)

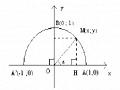
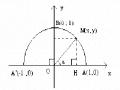
Giải: Giải phương trình (1) dưới "khía cạnh" đồ thị, nhờ vào cách đặt X = cosx,

Y = sinx. Khi đó, nghiệm của phương trình 3 .sinx + cosx = 2 có dạng đồ thị là một đường thẳng: 3 .Y + X = 2.

Mặt khác, nhờ vào "mối quan hệ" giữa cosx và sinx theo hằng đẳng thức lượng giác cơ

bản: cos2x + sin2x = 1, hay X2 + Y2 = 1 có đồ thị là đường tròn đơn vị.

- Vẽ đường thẳng (D): 3 .Y + X = 2 và đường tròn đơn vị (C): X2 + Y2 = 1 vào cùng một hệ trục tọa độ OXY.

Y

B

M

A'

-1

X

0

1

2

A 1

3Y  X 2

Đường thẳng (D): 3 Y + X = 2 cắt đường tròn đơn vị (C): X2 + Y2 = 1 tại điểm M có

3

tọa độ: X = 1 , Y =

2 2

Hay cosx =

1, sinx =

2

3.

2

- Giải hệ phương trình:

B'

Hình 2.24

cosx = 1/2 và sinx = 3 /2  x =

+ k.2, k Z.

3

VD 3: Cho ngũ giác đều ABCDE có tâm O. A

Chứng minh: v

Giải:

O

D

Hình 2.25

C

OA OB OC OD OE 0

E

B

Cách 1: Từ giả thiết ABCDE đều

nên OA là trục đối xứng của B và E, của

D và C. Do đó:

mOA OB OE kOA OC OD

Do đó: v

OA OBOC OD OEOA (1m k)

Chứng minh tương tự ta cũng được: v

OB (1m k)

Nên v cộng tuyến với hai vectơ không cộng tuyến, nên

Cách 2: Vì ABCDE đều nên:

v 0.

OA OB kOD OB OC kOE OC OD kOA

OD OE kOB

OE OA kOC

(víi

k 0)

Cộng từ vế của các đẳng thức trên, ta có: 2 v = k v

Để ý rằng k < 0 nên v có hướng ngược với chính nó. Vậy v 0.

Cách 3: Từ giả thiết ABCDE đều nên AB  OD và

OA OB kOD

OE OC mOD

Khi đó: v

OAOBOCODOEkODmODOD = OD

(k m 1)

AB.v AB.OD.(k m 1) 0

Chứng minh tương tự, ta cũng có:

BC.v 0

mà BC, AB

là hai vectơ không cộng





tuyến, nên: 



AB.v 0 

BC.v 0

AB v





BC v

v 0

Cách 4: Từ giả thiết ABCDE đều nên OA = OB = OC = OD = OE, suy ra:

OA.v OA2OA2cos(OA,OB) OA2cos(OA,OC) OA2cos(OA,OD)OA2cos(OA,OE)

= OA(1 2cos 22cos 4)

5 5

Chứng minh tương tự, ta cũng có: OB.v OB 2 (1 + 2cos 2+ 2cos 4)

5 5

Do đó: OA.v OB.v AB.v 0 AB v .

Suy luận tương tự, ta cũng có

BC 

v . Mà A, B, C không thẳng hàng nên

v 0.

Cách 5: Xét phép quay tâm O, góc quay

2.

5

Ta có: AB

B C

C D

D E

E A

Như thế, Q

2 

5

0 ( v ) = v . Vậy v có hai hướng phân biệt nên v 0.

Cách 6: Xét phép chiếu song song phương (AO) xuống DC. A

Ta có:

A,OI

E K E O B

D D 

B H K I H

C C D C

Hình 2.26

Do ABCDE đều nên OA là trục đối xứng của B và E, của D và C, suy ra:

v ' =

II IH IC ID IK 0

v ' là hình chiếu của vectơ v qua phép chiếu song song phương (AO) xuống đường thẳng DC, theo tính chất của phép chiếu vectơ, suy ra v //(AO).

Chứng minh tương tự ta cũng có v //(BO).

Mà A, B, O không thẳng hàng nên

v 0.