Phát triển tư duy biện chứng của học sinh trong dạy học Hình học ở trường trung học phổ thông - 16

v = k a

v = k b

( a, b không cộng tuyến)

v a v b

( a, b không cộng tuyến)

v =k v

k 1

Q ( v )= v

Có thể bạn quan tâm!

• Phát triển tư duy biện chứng của học sinh trong dạy học Hình học ở trường trung học phổ thông - 13
• Phát triển tư duy biện chứng của học sinh trong dạy học Hình học ở trường trung học phổ thông - 14
• Biện Pháp 2 : Làm Cho Học Sinh Biết Xem Xét Các Đối Tượng Toán Học Dưới Nhiều Khía Cạnh Khác Nhau Và Xem Xét Đối Tượng Toán Học Trong Mối Liên Hệ
• Phát triển tư duy biện chứng của học sinh trong dạy học Hình học ở trường trung học phổ thông - 17
• Phát triển tư duy biện chứng của học sinh trong dạy học Hình học ở trường trung học phổ thông - 18
• Biện Pháp 3 : Làm Cho Học Sinh Biết Phát Hiện Những Bước Thay Đổi Từ Sự Biến Đổi Về Lượng Sang Biến Đổi Về Chất

Xem toàn bộ 225 trang tài liệu này.

11

0

4

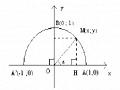
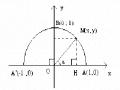
Chiếu theo hai phương phân biệt có hình chiếu đều bằng

(3)

vectơ v 0

Sơ đồ 2.1

Quá trình phân tích tìm được các cách giải trên có thể được thể hiện bằng sơ đồ trên.

Cách 7: Ta có: v 2= ( OAOBOCODOE)2 =

= 5OA2 + 2OA2(2cos 2+2cos 4) + 2OA2(cos 2+2cos 4) +

5 5 5 5

+ 2OA2(cos 2+cos 4) + 2OA2.cos 2= 5OA2 + 10OA2(cos 2+cos 4).

5 5 5 5 5

Mặt khác, ta chứng minh được: cos 2+cos 4= 1

5 5 2

Vậy: v 2 = 0  | v | = 0 nên v 0.

Không phải BT nào chứng minh một vectơ bằng vectơ  không ta cũng có thể giải như VD 3 ở trên.

Như vậy để chứng minh một vectơ là vectơ - không điều kiện đầu tiên ta định hướng có thể có các cách như ở (2), đây chính là ta nhìn BT dưới dạng chính quy mẫu mực. Tuy vậy, phải dựa vào đặc thù riêng lẻ của BT mà ta có thể tìm được các cách giải khác nhau đó chính là (3).

Cũng có khi từ các cách giải khác nhau đó ta có thể tìm được BT mới. Chẳng hạn, từ lời giải cách 4 ta tìm được một BT mới.

Chứng minh: * 1 + 2cos 2+ 2cos 4= 0

5 5

* 4cos2 2+ 2cos 21 = 0

* 4sin2

5

+ 2sin

10

5

1 = 0

10

* cos 2=

5

5 1

4

115

* sin =

10

5 1 .

4

Với các ý tưởng trên ta có thể mở rộng lời giải cho đa giác đều 2n + 1 cạnh.

Trên cơ sở so sánh các trường hợp riêng lẻ, dùng phép tương tự để chuyển từ trường hợp riêng này sang trường hợp riêng khác, khai thác mối liên hệ mật thiết với trừu tượng hóa, làm rõ mối quan hệ chung riêng giữa mệnh đề xuất phát và mệnh đề tìm được bằng đặc biệt hóa và hệ thống hóa, ta có thể tập luyện cho học sinh khái quát hóa tài liệu Toán học, tạo khả năng tìm được nhiều giải pháp trên nhiều góc độ và tình huống khác nhau, khả năng tìm ra những mối liên hệ trong những sự kiện bên ngoài tưởng chừng như không có liên hệ với nhau, khả năng tìm ra giải pháp lạ và duy nhất. Các HĐ này góp phần rèn luyện tính nhuần nhuyễn cũng như tính nhạy cảm vấn đề của TD.

Quan điểm trên chỉ rõ trong quá trình DH GV phải cung cấp cho HS những tri thức về PP để HS có thể tự mình tìm tòi, tự mình phát hiện và phát biểu vấn đề, dự đoán được các kết quả, tìm được hướng giải của một BT, hướng chứng minh một định lí, giúp HS hiểu sâu sắc bản chất các khái niệm, các mệnh đề, ý nghĩa và nội dung các công thức, các chứng minh, từ đó mà nhớ lâu các kiến thức Toán học và nếu quên thì có thể tìm lại được.

VD 4: Trong mặt phẳng tọa độ, cho tam giác ABC có các đỉnh A(4 ; 1), B(2 ; 4), C(2 ;

2). Gọi O, G, H lần lượt là tâm đường tròn ngoại tiếp, trọng tâm, trực tâm của tam giác đó. Chứng minh H, G, O thuộc cùng một đường thẳng [126, tr. 52].

Giải:

Cách 1: Xem xét mối quan hệ H, G, O trên khía cạnh tọa độ

Trọng tâm G có tọa độ:

x x A xB xC G3

 4  2  2  0 ;

3

yG 

y A yB yC

3

 1  4  2  1

3

G(0 ; 1).

Gọi tọa độ trực tâm H là (x ; y).

(4 ; 1)A

116

4

Ta có: AH = (x+4 ; y1); BC = (0 ; 6)

AH BC AH .BC  0

0(x + 4) 6(y 1) = 0

y = 1.

Ta lại có: BH = (x2 ; y4), AC = (6 ; 3).

BH AC BH .AC  0

OG 1 H O

2

Hình 2.27

2 x

C(2 ; 2)

6(x 2) 3(y 4) = 0 6x 3y = 0 2x y = 0

Vì y = 1 nên suy ra: x =

1 H( 1 ; 1).

2 2

Tâm O(x ; y) của đường tròn ngoại tiếp ABC thỏa mãn hệ thức OA = OB = OC.

OA2 = OB2 = OC2

Do vậy tọa độ (x ; y) của O là nghiệm của hệ:

OA2OB2

2 2



OB OC

x  42y  12x  22y  42



x  22y  42x  22y  22

12x  6 y  3  0



y  1  0

x 1 1







4

y  1

O



;1

4 

Ta có: GH 1 GO  1;0

Suy ra GH 2GO .

4

= ( ;0) , 

2 

Vậy H, G, O thuộc cùng một đường thẳng.

A

H

G

O

M

Cách 2: Xem xét mối quan hệ giữa H, G, O trên khía cạnh vectơ

Gọi M là trung điểm BC, K là điểm đối xứng với B qua O.

K Xét ABK ta có: O là trung điểm BK và OA = OB = OK hay tam giác

B C này có đường trung tuyến ứng với

Hình 2.28 1

cạnh huyền bằng

2

cạnh huyền; do đó ABK là tam giác vuông tại A.

Suy ra: AB AK. Mặt khác: CH AB AK // CH (1)

Ta lại có: AH BC ,

CK BC (vì BCK nhìn đường kính BK), do đó AH // CK (2) Từ (1) và (2) suy ra AHCK là hình bình hành.

Do đó: AH KC . Ta lại có: OM =

1 KC OM = 1 AH

Và GH GA AH

2 2

= 2 GM KC

= 2 GM + 2 OM = 2 OM + 2 MG = 2( OM + MG ) = 2 OG GH 2GO .

Vậy H, G, O thuộc cùng một đường thẳng..

Cách 3: Xem xét mối quan hệ giữa H, G, O trên khía cạnh góc

Gọi M là trung điểm của BC.

Ta đã có A, G, M thẳng hàng và GM

GA

1 ,

2

(Do AH // OM, các góc so le trong). Gọi K là điểm đối xứng với B qua O.

A

Suy ra OM =

1 CK.

2

Ta chứng minh được AHCK là hình bình hành

nên: AH = CK = 2OM. H K

Xét GHK và GOM, ta có: G O

GM GO 1 BC



GA GH 2

và OMG = HAG.

OMG= HAG.

M

Hình 2.29

Suy ra

AGH ~ MGO 

MGO = AGH;

mà hai góc này ở vị trí đối đỉnh nên 3 điểm H, G, O thẳng hàng.

Cách 4: Xem xét mối quan hệ giữa H, G, O trên khía cạnh tỉ số các đoạn thẳng

Gọi M là trung điểm của BC, K là điểm đối xứng với B qua O.

H

G O



A

K

B C

M

Hình 2.30

Nhận thấy: AH // OM, ABK có OA = OB = OK nên ABK là tam giác vuông tại

A. Ta có:

AB AK

và AB HC

nên suy ra AK // HC.

AHCK là hình bình hành AH = KC.

Ta lại có: KC = 2OM (do tính chất đường trung bình trong tam giác)

AH = KC = 2OM AH

OM

 2 ; mà GA

GM

 2 nên suy ra GA

GM

AH OM

 2 .

Do đó theo định lí Talet thì ta có H, G, O thẳng hàng.

VD 5: Cho ABC. Gọi ma là độ dài đường trung tuyến ứng với cạnh BC = a.

Chứng minh công thức đường trung tuyến:

2 b c

a [126, tr. 58].

ma

2 2

2

2 4

Giải: Gọi AI là đường trung tuyến vẽ từ A của tam giác ABC.

A

c

m

b

a

Cách 1: Nhìn nhận vấn đề cần chứng minh dưới góc độ áp dụng kiến thức vectơ

Ta có: b2 + c2 = AC2 + AB2

= AC 2 + AB 2 = ( AI + IC )2 + ( AI IB )2

= AI 2 + IC 2 + 2 AI.IC + AI 2 + IB 2 + 2 AI.IB

= 2 AI 2 + IC 2 + IB 2 + 2 AI .( IC IB ) B C

a I

a

= 2 m2

+ a 2

4

+ a 2

4

+ 0 (Vì

IC IB = O )

Hình 2.31

a

= 2 m2

+ a 2

2

. Suy ra:

2 b 2 c 2

m



a2

a 2

4

(đpcm).

Cách 2: Nhìn nhận vấn đề cần chứng minh bằng cách sử dụng tích vô hướng của hai vectơ và định lí côsin trong tam giác

Trước hết, ta biểu diễn AI qua AB và AC .

Ta có: AI =

1 ( AB + AC ) (vì I là trung điểm của BC)

2

m AI =



2 2 1 ( AB + AC )2 =

a4

1 ( AB 2 + AC 2 + 2 AB.AC )

4

Mặt khác ta lại có:

AB.AC =

AB . AC .cos A

AB.AC c.b.

b2 c 2 a 2

2bc

= 1 (b2

2

+ c2

 a2). Vì vậy:

m 2 =

1 (c2

4

+ b2

+ 2. 1

2

(b2

+ c2 

a2)) =

1 (2b2 + 2c2  a2) 

2 b c a

a

(đpcm).

2 2

2

4 ma 2 4

Cách 3: Chứng minh bằng cách sử dụng PP đồng dạng

Trước hết ta chứng minh mệnh đề sau: “Trong một hình bình hành, tổng bình phương các đường chéo gấp đôi tổng bình phương hai cạnh liên tiếp”.

Ta cần chứng minh: AC2 + BD2 = 2(AB2 + AD2) K

Thật vậy: Dựng CH AD, BK AD

Khi đó, ABK = DCH (cạnh huyền, cạnh góc vuông)

AK = DH. Theo định lí Pitago, ta có: B

AC2 = CH2 + (AD  DH)2 (1)

BD2 = BK2 + (AD + AK)2 = CH2 + (AD + DH)2 (2)

Cộng (1) và (2) vế theo vế, ta có:

A H D

Hình 2.32 C

A

c

m

b

a

I

a

AC2 + BD2 = 2CH2 + 2AD2 + 2DH2 = 2(CH2 + DH2) + 2AD2

= 2DC2 + 2AD2 = 2AB2 + 2AD2 = 2(AB2 + AD2)

B C

Áp dụng vào BT tính ma:

Ta có: BC2 + AJ2 = 2(AB2 + AC2)

a2 + AJ2 = 2(b2 + c2) Với AJ = 2AI = 2ma

a2 + 4 2 2 2

2 b 2 c 2 a 2 J

ma = 2(b

+ c ) ma 2 4 .

Hình 2.33

VD 6: Viết phương trình đường tròn đi qua ba điểm M(2 ; 4), N(5 ; 5), P(6 ; 2) [126, tr. 95].

Cách 1: Giả sử phương trình đường tròn có dạng:

x x02y y02R 2(*).

Do M, N, P thuộc đường tròn nên ta có hệ phương trình với 3 ẩn a, b, c:

 2 x0

0



24 y

2R 2

0

5 x0

25 y 2R 2



0

0

6 x

2 2 y

2R 2

x 2 y 2 R 2  4x  8 y

 20  0

1

0 0 0 0

0

0

0

x 2 y 2 R 2  10x  10 y

0

 50  0

2

(I)

x 2 y 2 R 2  12x  4 y

 40  0

3

0 0 0 0

Lấy (1) (2) ta được: 14x0  2 y0  30  0

 7x0 y0  15  0

y0  15  7x0

Lấy (2) (3) ta được: 2x0  14 y0  10  0

x0  7 y0  5  0 x0  715  7x0  5  0

x0  105  49x0  5  0  50x0  100 x0  2

y0  15  7.2  1

x0  2



0

(I) y  1



R 25  225  12 9  16  25

Vậy, phương trình đường tròn cần tìm là: x  22y  12 25 .

Cách 2: Giả sử phương trình đường tròn có dạng:

x 2 y 2  2ax  2by c  0 , điều kiện: a2 + b2 c > 0.

Do M, N, P thuộc đường tròn nên ta có hệ phương trình với 3 ẩn a, b, c:

4  16  4a  8b c  0

 4a  8b c  20  0

a 2

25  25  10a  10b c  0 

 10b c  50  0 

1

thỏa điều kiện.





36  4  12a  4b c  0

10a



12a  4b c  40  0

b



c 20

Vậy, phương trình đường tròn cần tìm là: x 2 y 2  4x  2 y  20  0 .

Cách 3: Gọi I(x ; y) và R là tâm và bán kính của đường tròn qua 3 điểm M, N, P.

Từ điều kiện: IM = IN = IP

IM

IN

IM 2IN 2

x  22y  42x  52y  52



IM

IP

IM 2IP 2

x  22y  42x  62y  22





x 2 4x y y 2 8 y  16 x 2 10x  25 y 2 10 y  25



x 2 4x y y 2 8 y  16 x 2 12x  36 y 2 4 y  4

4x  8 y  10x  10 y  30  0 14x  2 y  30  0 7x y  15  0



4x  8 y  12x  4 y  20  0 x  12 y  20  0 x  6 y  10  0

16 8



y  15  7x

8x  6(15  7x)  10  0

50x  100



y  15  7x

x  2



y  1

I(2; 1)

R2= TM2= 16 + 9 = 25. Phương trình đường tròn cần tìm là: x  22y  12 25 .

d1

M

H



N

I

.

K

d

P

Cách 4: Viết phương trình đường trung trực d1 của đoạn thẳng MN. Gọi H là trung điểm của đoạn MN.

x  2  53



H2

y



4  5





H2

2 3; 9

H

2





9  2 2

2

MN 7;1là vectơ pháp tuyến của d1.

Hình 2.34

Phương trình d :

3 

9  0

1 7x



1y 

2

2



 7x y 21 9  0 7x + y  15 = 0 (d1)

2 2

Viết phương trình đường trung trực d2 của đoạn NP: Gọi K là trung điểm của NP:

x5  6 11

K 2 2

y





5  2 3





K 2 2

113

K

2



; 

2 

NP 1;7là vectơ pháp tuyến của d2.

Phương trình d :

11 

3  0

2 1x



7y 

2

2



Xem tất cả 225 trang.