Rèn Và Phát Triển Tư Duy Biện Chứng Cần Chú Trọng Tới Việc Rèn Luyện, Bồi Dưỡng Cách Thức Tìm Tòi Và Vận Dụng Kiến Thức Của Từng Lĩnh Vực Toán

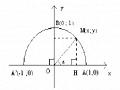
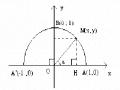
b2 = a2 + c2 2ac.cosB (2)

c2 = a2 + b2 2ab.cosC (3) (đây chính là vấn đề cần phát hiện và phát biểu lên).

* GV xác nhận thành quả của HS và tiếp tục hướng dẫn HS chứng minh vấn đề đã phát hiện ra:

GV: Các hệ thức mà các em vừa tìm ra được cho tam giác bất kì (trong BT 3) là đúng. Các hệ thức đó chính là nội dung của định lí hàm số côsin.

Bây giờ em nào hãy sử dụng vectơ để chứng minh định lí này?

GV: Các em hãy viết công (1) nhờ ngôn ngữ vectơ? từ đó hãy tìm cách chứng minh nội dung công thức (1).

Lời giải: a2 = b2 + c2 2bc.cosA

Có thể bạn quan tâm!

• Những Biểu Hiện Của Tdbc Trong Dạy Học Môn Hình Học Ở Trường Thpt
• Nội Dung Môn Dạy Học Hình Học Ở Trường Phổ Thông
• Những Căn Cứ Của Việc Đề Ra Các Biện Pháp Rèn Luyện Và Phát Triển Tư Duy Biện Chứng Cho Học Sinh
• Phát triển tư duy biện chứng của học sinh trong dạy học Hình học ở trường trung học phổ thông - 13
• Phát triển tư duy biện chứng của học sinh trong dạy học Hình học ở trường trung học phổ thông - 14
• Biện Pháp 2 : Làm Cho Học Sinh Biết Xem Xét Các Đối Tượng Toán Học Dưới Nhiều Khía Cạnh Khác Nhau Và Xem Xét Đối Tượng Toán Học Trong Mối Liên Hệ

Xem toàn bộ 225 trang tài liệu này.

BC 2 AC 2 AB 2 - 2 | AC | . | AB | .cos(AB, AC)

BC 2

AC 2 AB 2 - 2AC.AB

BC 2 (AC - AB)2

Từ đó HS có thể chứng minh được công thức (1) như sau:

BC (AC - AB) 

BC 2 (AC - AB)2 

BC2 AC2 AB2 - 2AB.AC

= AC2 + AB2  2 | AC | . | AB | .cos (AC, AB)  a2 = b2 + c2  2bc.cosA

Việc chứng minh công thức (2) và (3) là tương tự chứng minh trên. Sau đó GV hướng dẫn cho HS phát biểu lại toàn bộ nội dung của định lí hàm số côsin và làm các bài tập ứng dụng.

Về thực hành giải toán, cần coi trọng các bài tập trong đó chưa rõ điều phải chứng minh, HS phải tự lập, tự tìm tòi để phát hiện vấn đề và giải quyết vấn đề. Hướng dẫn HS khai thác, khám phá những kết quả từ các BT đã giải.

2.4.4. Rèn và phát triển tư duy biện chứng cần chú trọng tới việc rèn luyện, bồi dưỡng cách thức tìm tòi và vận dụng kiến thức của từng lĩnh vực Toán học cho học sinh

Toán học có tính thống nhất cao, nhưng cũng có tính đa dạng. Các bộ phận Toán khác nhau và chúng đều mang tính độc lập, như có cấu trúc, suy luận, chứng minh, ... cả cách thức riêng trong tìm tòi, phát hiện kiến thức mới. Vì vậy, cùng với hệ thống khái niệm (với tư cách là cơ sở của các PP nhận thức), HS cần được rèn luyện, bồi

dưỡng cách thức tìm tòi và vận dụng kiến thức của từng lĩnh vực Toán học. Nếu HS không nắm vững các cách thức nói trên thì không thể học tập, tạo ra cái mới. Cái mới đó không chỉ là kiến thức, kĩ năng chưa biết đối với HS mà còn là cách thức, PP tìm ra cái chưa biết.

2.4.5. Rèn luyện và phát triển tư duy biện chứng cho học sinh cần căn cứ vào thành tựu nghiên cứu về tư duy biện chứng của Tâm lí học, Giáo dục học hiện đại Vì TD sáng tạo [75, tr. 72 - 99] là một dạng của TDBC và nó có ba yếu tố đặc

trưng là: tính mềm dẻo, tính nhuần nhuyễn và tính nhạy cảm vấn đề. Mỗi yếu tố đó có một số đặc trưng riêng.

- Tính mềm dẻo của TD có các đặc trưng:

+ Dễ dàng chuyển từ HĐ trí tuệ này sang HĐ trí tuệ khác.

+ Suy nghĩ không rập khuôn.

+ Nhận ra vấn đề mới trong điều kiện quen thuộc; nhìn thấy chức năng mới của đối tượng quen biết.

- Tính nhuần nhuyễn của TD có đặc thù riêng, thể hiện ở các khả năng:

+ Tìm được nhiều giải pháp trên nhiều góc độ và tình huống khác nhau.

+ Xem xét đối tượng dưới những khía cạnh khác nhau.

- Tính nhạy cảm vấn đề của TD có các đặc trưng sau:

+ Nhanh chóng phát hiện vấn đề.

+ Phát hiện ra mâu thuẫn, sai lầm, thiếu lôgic, chưa tối ưu từ đó có nhu cầu cấu trúc lại, tạo ra cái mới.

Yêu cầu này chỉ đạo GV trong quá trình DH theo định hướng phát triển TDBC cho HS cần căn cứ vào thành tựu nghiên cứu về TD của Tâm lí học hiện đại để từ đó xây dựng được nội dung DH và đề ra được PPDH phù hợp, có tác động đến các yếu tố đặc trưng của TD dựa trên vốn tri thức đã có của HS và vừa phù hợp với lứa tuổi của HS.

Như vậy các yêu cầu trên đây muốn đạt được phải dựa vào các yếu tố sau:

- Tổ chức những HĐ Toán học thích hợp (phát hiện mâu thuẫn mở rộng, nâng cao, đào sâu, ...) trong quá trình DH toán nhằm hướng dẫn HS TD theo các quy luật của lôgic BC (tính khách quan, tính toàn diện, ...).

- Đến một chừng mực nào đó, HS đã hiểu các quy luật lôgic BC ở dạng ẩn tàng, tập cho HS vận dụng các quy luật này vào việc học các khái niệm, các định lí và giải bài tập Toán.

- Rèn luyện TDBC cần kết hợp hữu cơ, mối quan hệ BC giữa các thao tác TD như: Phân tích và tổng hợp, qui nạp và diễn dịch, cụ thể và trừu tượng.

- Căn cứ vào cấu trúc, nội dung các kiến thức trong SGK HH, phát hiện các yếu tố TDBC chứa đựng trong các bài dạy, để đưa ra những HĐ thích hợp nhằm vừa rèn luyện TDBC, nhưng phải đạt mục tiêu, yêu cầu bài dạy.

- Rèn lyện TDBC phải căn cứ vào mức độ, yêu cầu của chưng trình, SGK và trình độ HS trong từng lớp mà đưa ra các HĐ phù hợp.

- Các biện pháp thực hiện rèn luyện và phát triển TDBC phải cụ thể, dễ thực hiện và sát chương trình.

2.5. Những biện pháp thực hiện nhằm góp phần rèn luyện và phát triển tư duy biện chứng cho học sinh thông qua dạy học Hình học ở trường THPT

Rèn luyện và phát triển TDBC là một quá trình lâu dài, còn nhiều khó khăn, chúng tôi mạnh dạn đề xuất một số biện pháp nhằm góp một phần vào việc rèn luyện và phát trển TDBC cho HS thông qua DH Hình học ở trường THPT:

2.5.1. Biện pháp 1: Làm cho học sinh biết xem xét các đối tượng Toán học trong cả quá trình lịch sử phát triển của nó và xem xét các đối tượng Toán học một cách khách quan để thấy nguồn gốc ra đời, điều kiện tồn tại, bản chất của các đối tượng

a. Làm cho học sinh biết xem xét các đối tượng Toán học trong cả quá trình lịch sử phát triển của nó

- TDBC hình thành cho HS quan điểm: "Khi xem xét sự vật, phải nhận thức sự vật trong sự phát triển, trong sự tự vận động của nó" là một quy luật cơ bản của TDBC.

- Trong DH Toán giúp HS nhận thấy được nhu cầu, tính "ưu việt" cũng như

"hạn chế" của kiến thức Toán học phát triển trong từng giai đoạn.

VD 1: Quá trình thình thành và phát triển để đi đến sự hoàn chỉnh của hàm số lượng giác: Tỉ số lượng giác của góc nhọn (HH 8), tỉ số lượng giác của góc bất kì (HH 10), các hàm số lượng giác (Đại số và Giải tích 10 nâng cao).

VD 2: Sự hình thành và phát triển của PPTĐ ở trường PT

- Hệ tọa độ afin (hệ tọa độ xiên)

Các loại hệ tọa độ (HTĐ) thường dùng: HTĐ afin, HTĐ Đêcac, HTĐ cực, HTĐ trụ, ... Ở đây ta chỉ xét HTĐ afin. HTĐ afin trong mặt phẳng(mp) gồm một điểm gốc O

và hai véctơ cơ sở độc lập tuyến tính {

e1 ,

e2 }. HTĐ afin trong KG gồm một điểm

gốc O và 3 vectơ cơ sở { e1 ,

e2 ,

e3 }.

Tọa độ afin của một điểm: Trong mp (KG), giả sử điểm M có:

OM 

xo e1 yo e2

( OM

 x o e1  y o e 2  z o e3 ) ta nói rằng điểm M có tọa độ

(xo, yo) ((xo, yo, zo)) đối với HTĐ afin {O;

e1, e2

}({O; e1, e2 , e3

}).

Các kiến thức khác: Phương trình đường thẳng trong HTĐ afin của mp, của KG, phương trình mp trong HTĐ afin của KG, ... Chẳng hạn, trong HTĐ afin của mp, hãy lập phương trình ba cạnh của ABC, cho biết A(1; 3) và hai đường trung tuyến xuất phát từ B và C có phương trình: x 2y + 1 = 0 và y 1 = 0. Giải ra ta có phương trình ba cạnh là AB: x y + 2 = 0; AC: x + 2y 7 = 0; BC: x 4y 1 = 0.

- Các tri thức khoa học (TTKH) sau đây cũng có liên quan đến PP toạ độ (PPTĐ) là: Tâm tỉ cự và trọng tâm của một họ hữu hạn điểm, tọa độ trọng tâm. Ý nghĩa HH của phương trình bậc nhất một ẩn, 2 ẩn và 3 ẩn. Về chùm đường tròn. Về giao tuyến côníc với dường thẳng. Về hướng của KG 3 chiều. Về các phép biến đổi tọa độ trong mp, KG, các phép dời hình trong mp, KG, nghiên cứu các thiết diện của các mặt, ...

*Tri thức giáo khoa của PPTĐ - Tri thức chương trình

HH sơ cấp là một ngành Toán học ra đời cách đây khoảng hơn vài nghìn năm với khối lượng kiến thức đồ sộ. Không thể đưa hết khối lượng kiến thức ấy vào dạy cho HS, vì vậy phải có một sự gạn lọc KH, tinh tế, hợp lí về mặt nội dung kiến thức cũng như về PP, có nhiều kiến thức HH trước đây đã có mặt trong một số SGK HH thì nay không còn trong SGK Hình học CCGD nữa.

TTKH còn phải sàng lọc mới trở thành tri thức giáo khoa (TTGK) quy định trong chương trình và SGK [74, tr. 72], [155, tr. 7], nghĩa là không phải là mọi TTKH đều được đưa vào giảng dạy trong nhà trường PT mà phải sàng lọc những TTKH với sự tác động của các nhà Toán học, nhà giáo dục, ... phải qua một quá trình chuyển hoá SP, khi đó mới có TTGK. Như vậy, tuỳ theo từng quốc gia mà sự lựa chọn chương trình đưa giảng dạy khác nhau để làm sao phù hợp với trình độ, khả năng "hấp thụ" kiến thức của TD HS với các quy luật của quá trình nhận thức. Bởi vậy có thể nói, TTGK là kết quả của quá trình chuyển hoá SP từ kiến thức KH sang kiến thức môn học.

Hệ trục tọa độ Đêcac vuông góc là một HTĐ afin đặc biệt: Trong mp(KG), HTĐ

afin {O;

e1,

e2 } ({O;

e1,

e2 , e3 }) trở thành một HTĐ Đêcac vuông góc nếu ta có | e1 |

= | e2 | = 1 và e1 e2 (| e1 | = | e2 | = | e3 | = 1 và e1 e2 , e2 e3 , e3 e1 ).

Nội dung chương trình HH ở PT trên mp: đường thẳng, đường tròn, 3 đường conic với các phương trình chính tắc và trong KG: đường thẳng, mp, mặt cầu. Ngoài ra, còn đưa vào chùm đường thẳng, mp, tích có hướng, ...

Các vấn đề được bỏ qua: tính chất quang học của các đường conic, phương trình tham số của mp. Việc áp dụng vectơ để giải các bài toán HH không được chú trọng nhiều, vì theo tinh thần giảm tải để tránh sự nặng nề cho HS.

* Tri thức dạy học [74, tr. 72]:

Sau khi đã có tri thức giáo khoa (TTGK) thì GV phải làm sao truyền thụ lại để HS lĩnh hội được tri thức này. Để đạt được mục tiêu, người GV bằng vốn tri thức và PP tài nghệ của mình thực hiện quá trình chuyển hoá SP, biến TTGK thành tri thức của chính mình và truyền thụ tri thức đó cho HS nhằm biến tri thức đó thành tài sản của riêng họ. GV nói chung không dạy nguyên dạng TTKH hay TTGK mà phải chuyển hoá TTGK thành Tri thức dạy học. Nắm vững TTKH là một điều kiện cần nhưng chưa đủ để đảm bảo kết quả DH.

- Sự hình thành và phát triển của PPTĐ ở trường PT

Người đầu tiên sử dụng PPTĐ là Đêcac - nhà Triết học kiêm Vật lí và Toán học người Pháp (1596 - 1650).

Tuy nhiên, việc đại số hoá HH sẽ làm cho HS không được rèn luyện nhiều về trí tưởng tượng KG (chẳng hạn, cho hai đường thẳng trong KG là cho phương trình của chúng. Muốn xét vị trí tương đối giữa các đường thẳng đó, HS không cần có một hình dung trực quan nào, mà chỉ cần dựa vào các vectơ chỉ phương của chúng. Cho tọa độ của một điểm và cho phương trình của một mp thì dùng công thức đã biết, HS tính ngay được khoảng cách từ điểm đó tới mp mà không cần tới một chút tưởng tượng nào.

Vì HS đã học HH 11 một cách trực quan, nên các kiến thức đã biết có thể giúp họ nhìn các BT ở Lớp 12 một cách dễ dàng hơn.

HH và Đại số là hai ngành khác nhau của Toán học, nhưng với PPTĐ người ta đã đưa hai ngành đó xâm nhập vào nhau và tạo điều kiện giúp nhau cùng phát triển.

Bằng PPTĐ chúng ta có thể trình bày nhiều nội dung HH ở bậc PT mà không dựa vào hình vẽ. Chẳng hạn, trong mp với HTĐ Đêcac vuông góc cho trước, ta có thể cho điểm (xo, yo), cho đường thẳng ax + by + c = 0, cho đường tròn

(x  a)2 + (y  b)2 = r2, cho nửa mp: mx+ ny + p  0, ...

Chúng ta có thể biểu thị nhiều hình khác nhau trong mp bằng một số phương trình và bất phương trình.

Các định lí HH có thể chuyển thành những quan hệ đại số giữa các con số, các chữ và các phép toán đại số.

Sự ra đời của PPTĐ đã lập được mối quan hệ mật thiết giữa HH và đại số. Người ta xem đây là một cuộc cách mạng trong Toán học vì nó giúp cho Toán học nói chung và HH nói riêng thoát ra khỏi cái TD cụ thể của KG Vật lí để đạt tới đỉnh cao của sự trừu tượng và khái quát.

Trong phần cuối công trình triết học lớn của Đêcac xuất bản năm 1637, ông đã trình bày về PPTĐ và những ứng dụng của PP này trong việc giải toán HH.

Phát triển tư tưởng của Đêcac, môn HH giải tích đã ra đời, cung cấp cho chúng ta PP nghiên cứu HH bằng công cụ đại số.

Trên cơ sở của sự phát triển và hoàn chỉnh của môn HH giải tích, những tư tưởng của PPTĐ đã khai sinh ra các chuyên ngành Toán học mới.

Ngày nay, trong chương trình HH của trường PT, HS được học về vectơ, các phép toán về vectơ và dùng vectơ làm phương tiện trung gian để chuyển các khái niệm HH và các mối quan hệ giữa các đối tượng HH sang các khái niệm, quan hệ đại số.

Mặt khác, với PPTĐ dùng trong các KG 1 chiều, KG 2 chiều, KG 3 chiều, chúng ta có thể mở rộng cho KG n chiều.

Thực vậy, khi khái niệm "chiều" theo nghĩa vật lí được trừu tượng hoá và mở rộng, ta được khái niệm "chiều" theo nghĩa Toán học. Và như vậy ta xây dựng được khái niệm về KG n chiều và có thể nghiên cứu HH của các KG đó.

Ngày nay, ở bậc đại học, các sinh viên đã được làm quen với các KG n chiều như: không vectơ n chiều, không afin n chiều, KG Ơclít n chiều, KG xạ ảnh n chiều và các KG phi Ơclít n chiều. Trong các KG n chiều đó, các khái niệm đường thẳng, mp đã được

khát quát hoá thành khái niệm m  phẳng. Khi nghiên cứu HH phẳng và HH KG ở trường PT bằng PPTĐ, chúng ta đã dùng các số thực và các phép toán của trường số thực.

Nói cách khác, bằng PPTĐ chúng ta đã xây dựng một "mô hình bằng số thực" để thể hiện các khái niệm và các quan hệ trong HH. Vì vậy, các tính chất của trường số thực như tính sắp thứ tự, tính liên tục đã được dùng để biểu thị các tính chất HH của các đối tượng trong HH.

Chẳng hạn, trên một đường thẳng d, nếu ta chọn một điểm O làm gốc tọa độ và một điểm E sao cho | OE | = 1 thì khi đó ta có một trục số.

d O E M(x)



Hình 2.5

Khi đường thẳng đã trở thành một trục số thì mỗi điểm M của đường thẳng sẽ tương ứng 11 với số thực xác định và ta suy ra tập hợp các điểm trên đường thẳng d cũng được sắp thứ tự và có tính chất liên tục.

Tương tự, trong mp, với một cặp hai số thực có thứ tự (x; y) ta có một điểm M duy nhất và ngược lại. Còn trong KG, với một bộ 3 số thực có thứ tự (x; y; z) ta cũng xác định được một điểm M duy nhất và ngược lại.

Do đó, người ta nói rằng, bộ môn HH đó được xây dựng trên trường số thực.

- Tri thức PP của PPTĐ

Kinh nghiệm cho thấy phần lớn HS đã quên khá nhiều các kiến thức ở lớp 10, cho nên GV cần đi chậm và thực hành nhiều trên lớp bằng các VD cụ thể. Các bài tập kiểu như sau có tác dụng ôn tập tốt: cho tọa độ ba đỉnh của một tam giác, tìm chu vi, tìm diện tích tam giác đó hoặc là tìm tọa độ trọng tâm, trực tâm và thâm chí cả tâm đường ngoại tiếp tam giác (mà chưa cần sử dụng phương trình đường thẳng trong các bài tập như thế; chẳng hạn nếu gọi (x; y) là tọa độ trực tâm H của tam giác ABC thì để

tìm x và y chỉ cần giải hệ phương trình:

AH.BC = 0 và

BH.AC

= 0, để tìm tọa độ tâm

I(x; y) của đường tròn ngoại tiếp chỉ cần giải phương trình IA = IB và IB = IC).

Xem tất cả 225 trang.