Phát triển tư duy biện chứng của học sinh trong dạy học Hình học ở trường trung học phổ thông

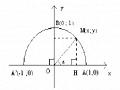
Hình 2.13

sin = y: tung độ của điểm M (HH 10)

sin =

y MH

(HH 9).

1 OM

b. Làm cho học sinh biết xem xét Toán học một cách khách quan để thấy nguồn gốc ra đời, điều kiện tồn tại cũng như các tính chất đặc trưng của các đối tượng (khái niệm, định lí, bài tập, ...)

- Ở đây TDBC là làm cho HS cảm nhận được tính "khách quan" của Lôgic BC: Một sự vật, hiện tượng tồn tại trong những điều kiện nhất định; phát hiện các tính chất đặc trưng phân biệt với các tính chất không đặc trưng để nhận thức sự vật, hiện tượng một cách đúng đắn, tránh chủ quan.

- Trong DH Toán cần làm cho HS nắm được con đường hình thành các khái niệm, định lí, giải toán chính xác, nắm được bản chất của khái niệm, giả thiết của định lí, điều kiện của BT. Từ đó hiểu sâu các đối tượng Toán học cần tiếp thu và khi vận dụng đỡ sai sót.

Chẳng hạn: Khi DH các khái niệm, các định lí, chú trọng quan tâm xây dựng các BT gốc tạo cơ sở để giải các BT nâng cao.

VD 1: Khi giải các BT liên quan tới vấn đề thẳng hàng. Để giúp HS có PP chứng minh ba điểm thẳng hàng, chúng ta cho HS làm BT cơ bản sau:

BT gốc: Ba điểm A, B, C phân biệt thẳng hàng khi và chỉ khi một trong các điều kiện sau được thỏa mãn:

a) AC 

kAB

b) Với O tùy ý: k  1 :

OC 

kOB

+ (1 k) OA

c) Với O tùy ý: k  1 : OA =

OC - kOB

1 k

d) Với O tùy ý:

OC 

kOB

+ l OA , trong đó k + l = 1

Giải: a). A, B, C thẳng hàng 

AC, AB

cùng phương  tồn tại duy nhất số

thực k sao cho

AC 

kAB .

b). Theo câu a), A, B, C thẳng hàng 

AC 

kAB

 với O tùy ý

OC - OA

k(OB - OA) 

OC kOB (1 - k)OA

c). Theo câu b). Ta có A, B, C thẳng hàng  với O tùy ý:

OC kOB (1 - k)OA

Đặt 1k = l thì

OC kOB

+ l OA với k + l = k + 1 k = 1

Các BT về chứng minh ba điểm thẳng hàng có thể các điểm đã cho biết thỏa mãn một số đẳng thức vectơ, khi đó cần biến đổi các đẳng thức vectơ này về dạng các đẳng thức đã nêu ở BT cơ bản để chứng tỏ các điểm thẳng hàng. Có thể nó là BT HH phẳng khi đó ta có thể hướng dẫn cho HS giải bằng PP vectơ. Trước hết cần "phiên dịch" các điều kiện của BT ra "ngôn ngữ" vectơ, sau đó mới biến đổi các đẳng thức vectơ thu được về dạng các dạng đẳng thức vectơ tương đương với điều kiện ba điểm thẳng hàng (ở BT gốc).

BT 1: Cho tam giác ABC. M và N là hai điểm xác định như sau:

MA 3MC 0 và NA 2NB 3NC 0

Chứng minh ba điểm M, N, B thẳng hàng.

Giải: Theo bài ra:

MA 3MC

0 

BA - BM 3(BC - BM) 0

4BM

BA 3BC

(1)

Theo bài ra:

NA 2NB 3NC

0 BA - BN - 2BN 3(BC - BN) 0

6BN

BA 3BC

(2)

Từ (1) và (2) ta có:

4BM

6BN 

BM 3 BN . Suy ra: B, M, N thẳng hàng.

BT 2: Cho tứ giác ABCD. Gọi M, N, P lần lượt là các điểm đối xứng với D đối với trung điểm các cạnh của tam giác ABC. Chứng minh rằng: điểm D và trọng tâm các tam giác ABC và MNP thẳng hàng.

Giải: Gọi Ao, Bo, Co lần lượt là trung điểm các cạnh BC, CA, AB; G1, G2 tương ứng là trọng tâm các tam giác ABC và MNP.

Ta có:

DG1

1 (DA DB DC) 3

2 3
Theo bài ra: M đối xứng với D đối với Ao nên:	DM DB DC	(3)
N đối xứng với D đối với Bo nên:	DN DC DA	(4)
P đối xứng với D đối với Co nên:	DP DA DB	(5)

Có thể bạn quan tâm!

Xem toàn bộ 225 trang tài liệu này.

1 (DM DN DP)

(1)

(2)

Thay (3), (4), (5) vào (2) ta có:

DG 2

2 (DA DB DC) (6)

Từ (1), (6) ta có:

DG1 

1 DG

2 2

. Suy ra: D, G1, G2 thẳng hàng.

BT 3: Cho tam giác ABC nội tiếp trong đường tròn tâm O. Qua ba đỉnh A, B, C vẽ các đường thẳng song song với nhau cắt đường tròn (O) lần lượt tại A1, B1, C1.

Chứng minh ba trọng tâm của tam giác ABC1, BCA1, CAB1 thẳng hàng.

Giải: Gọi G1, G2, G3 lần lượt là trọng tâm của ba tam giác ABC1, BCA1, CAB1.

Ta có: OG1

1 (OA OB OC ) 31

(1)

OG 2

OG 3

1 (OB OC OA ) 31

1 (OC OA OB ) 31

(2)

(3)

Từ (1), (2): OG - OG 1 (OA - OA OC

- OC)

1 2 3 1 1

G 2 G1

1 (A

4 1

A CC 1

) (4)

Tương tự, từ (2), (3) ta có:

G 2 G 3

1 (BB

3 1

A1 A)

(5)

Theo bài ra: A1A // BB1 nên

CC1 // A1A nên

BB1 

CC1 

mA1 A

nA1 A

(6)

(7)

Từ (4), (7):

G 2 G1

1 (A

3 1

A nA1 A) 

n 1

A1 A

(8)

Từ (5), (6):

G 2 G 3

1 (mA

3 1

A A1 A) 

m 1

A1 A

(9)

Từ (8), (9): G G

n 1

G G

 G , G , G

thẳng hàng.

2 1 m 1 2 3

1 2 3

Tương tự BT 3 ta có BT 4:

BT 4: Cho tam giác ABC nội tiếp trong đường tròn tâm O.

Qua ba đỉnh A, B, C vẽ các đường thẳng song song với nhau cắt đường tròn (O) lần lượt tại A1, B1, C1.

Chứng minh ba trực tâm của tam giác ABC1, BCA1, CAB1 thẳng hàng.

BT 5: (Định lí Mênêlauýt)

Cho tam giác ABC. Trên các đường thẳng AB, BC, CA lấy các điểm M, N, P

sao cho

MA . NB . PC

1. Chứng minh M, N, P thẳng hàng.

MB NC PA

BT 6: Cho tứ giác ABCD. Gọi P, Q, R lần lượt là trọng tâm các tam giác ADB, BDC, CDA. Chứng minh rằng: điểm D là trọng tâm các tam giác ABC và tam giác PQR thẳng hàng.

Về góc độ Tâm lí và góc độ Triết học, việc thực hiện biện pháp này tạo cơ sở HS liên tưởng khi giải BT mới, BT khó. Đặc biệt các BT gốc là cơ sở để giải chuỗi các BT liên quan các BT khó. Thực hiện biện pháp này góp phần tạo năng lực huy động kiến thức cho HS.

VD 2: Về khái niệm "Khoảng cách giữa hai đường thẳng chéo nhau". Ngoài các khái niệm cơ bản như: đường vuông góc chung, khoảng cách từ một điểm đến một đường thẳng, khoảng cách từ một điểm đến một mặt phẳng, khoảng cách giữa một đường thẳng và một mặt phẳng song song, khoảng cách giữa hai mặt phẳng song song, ... , còn có các BT gốc sau đây:

BT 1: Cho hai đường thẳng a, b chéo nhau, (P) là mặt phẳng song song với a và chứa b. CMR khoảng cách giữa hai đường thẳng a và b bằng khoảng cách giữa đường thẳng a và mặt phẳng (P).

Chứng minh: Trên đường thẳng a lấy một điểm M bất kỳ. Gọi N là hình chiếu của M lên mặt phẳng (P). Gọi c là đường thẳng qua N và song song với a.

Gọi B = c  b. Gọi d là đường thẳng qua B và song song với MN. Vì a, c, d đồng phẳng nên gọi A = d  a.

Hình 2.14

Ta có: AB // MN  AB  (P)  AB b. Mặt khác: MN  (P)  MN  c

 AB  c  AB  a.

Do đó, AB là độ dài đoạn vuông góc

chung của a và b. Vì ABMN là hình chữ nhật

(theo cách dựng), dẫn đến AB = MN. Mà MN chính là khoảng cách giữa a và (P). Suy ra điều phải chứng minh.

Cụ thể: Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh bằng a, SA vuông góc với đáy và SA = a.

Tính khoảng cách giữa hai đường thẳng AC và SD.

Giải: Kẻ Dt // AC thì ta có AC // mp(S, Dt) nên khoảng cách giữa AC và SD cũng chính là khoảng cách giữa AC và mp(S, Dt). Kẻ AI  Dt, AE  SI.

Vì Dt // AC nên Dt  SA do đó Dt  (SAI). Vì AE  (SAI) nên Dt  AE, từ đó ta có AE  mp(S, Dt). Vậy AE là khoảng cách cần tìm.

Ta có: AI = OD =

a 2 (O - là tâm ABCD)

I E A B

D C

AE 2

 1

AS¸2

 1

AI 2

 1  1  3

a 2 a 2 2 a 2

a 3

nên AE2 = a2 / 3 AE 

a 3

Vậy khoảng cách giữa AC và SD là AE 

BT 2: Cho hai đường thẳng a, b chéo nhau, (P) là mặt phẳng song song với b chứa a, (Q) là mặt phẳng song song a chứa b. CMR khoảng cách giữa hai đường thẳng a và b bằng khoảng cách giữa hai mặt phẳng (P) và (Q).

Chứng minh: Dễ thấy hai mp(P) và

(Q) song song với nhau.

Trên đường thẳng a lấy một điểm M thì M  (P). Gọi N là hình chiếu

Hình 2.16

khoảng cách giữa hai mặt phẳng.

của M lên mp(Q), khi đó đoạn MN là

Mặt khác, theo BT 1 thì MN là khoảng cách giữa hai đường thẳng a và b. Suy ra điều phải chứng minh.

Cụ thể: Lăng trụ tam giác ABCA1B 1C1 có các mặt bên là hình vuông cạnh a.

Các điểm D, E lần lượt là trung điểm các đoạn BC, A 1C1. Tính khoảng cách giữa hai đường thẳng DE và AB1.

Giải: Gọi F là trung điểm của B 1C1. Ta có: DF // BB1 và EF // A1B 1 nên (DEF)

// (ABB 1A1). Do đó khoảng cách giữa hai đường thẳng DE và AB1 chính là khoảng

A C

A I I1

E C1

Hình 2.17

cách giữa hai mp(DEF) và (ABB 1A1).

Gọi I là trung điểm A 1B 1. Dễ thấy C 1I vuông góc với hai mặt phẳng (ABB 1A1) và (DEF) và cắt chúng lần lượt tại I, I1.

Bởi vậy, khoảng cách giữa hai mặt phẳng này là II1.

Theo định lí Talet phẳng ta có:

II 1 IC a 3 .

1 2 1 4

a 3

Vậy khoảng cách giữa hai đường thẳng DE và AB1 là

BT 3: Dựng đường thẳng vuông góc chung của hai đường thẳng chéo nhau a và

b. Sau đó tính độ dài đoạn vuông góc chung.

Đối với BT này yêu cầu dựng chính xác đường thẳng vuông góc chung của hai đường thẳng chéo nhau và tính đoạn vuông góc chung dựa theo các bước dựng.

Cụ thể: Cho tứ diện OABC, trong đó OA, OB, OC đôi một vuông góc và OA = OB = OC = a. Gọi I là trung điểm của BC.

Hãy tính khoảng cách giữa hai đường thẳng AI và OC.

Giải: Gọi J là trung điểm của OB, H là hình chiếu của O lên AJ. Qua H kẻ đường thẳng song song với OC cắt AI tại E, qua E kẻ đường thẳng song song với OH

và cắt OC tại F. Ta có: OC  (OAB) nên OC  OH.

H E

O F C

Vì I, J lần lượt là trung điểm của

BC, OB nên IJ // OC, do đó IJ  OH.

Hình 2.18

Ta lại có OH  AJ nên OH  AI.

Vì EF // OH nên EF  OC và EF  AI. Suy ra EF là đoạn vuông góc chung của OC và AI. Ta có EF = OH.

Trong tam giác vuông AOJ ta có:

OH 2

 1

OA2

 1

OJ 2

 1  1  5

a2 a2 a2

nên OH Hay

a 5

EF 

a 5

Vậy khoảng cách giữa hai đường thẳng AI và OC là

VD 3: Khái niệm vectơ [126, tr. 5]

EF 

Định nghĩa: “Vectơ là một đoạn thẳng có hướng”, nghĩa là trong hai điểm mút của đoạn thẳng, đã chỉ rõ điểm nào là điểm đầu, điểm nào là điểm cuối.

A B A B D M D M

C N C N

Các đoạn thẳng Các vectơ

Hình 2.19

Khi dạy định nghĩa này cần làm cho HS hiểu được các vấn đề sau:

- Nguồn gốc ra đời: Như ta đã biết, trong Vật lí cũng như trong thực tế có những đại lượng có hướng như vận tốc của một chất điểm, gia tốc, lực tác dụng vào một vật, …Trong tính toán, những đại lượng đó cần được biểu diễn, nhưng đó lại là các đại lượng có hướng, vậy thì phải biểu diễn chúng như thế nào? Khái niệm vectơ ra đời một phần bắt nguồn từ đó.

Như vậy, khái niệm vectơ được xuất hiện một cách tự nhiên chứ không phải là cái gì đó từ trên trời rơi xuống, hay từ trong đầu các nhà Toán học bật ra. ở sách giáo khoa mới, để HS có thể tự học được và hiểu rõ được vấn đề, tác giả đã liên hệ tới Vật lí để nói đến các đại lượng vô hướng và đại lượng có hướng bằng cách nêu một VD để thấy đại lượng “có hướng” là rất cần: Nếu chỉ biết một tàu thủy chạy thẳng đều với tốc độ 20 hải lí một giờ (đại lượng vô hướng) mà không nói rõ nó chạy theo hướng nào thì ta không thể biết sau 3 giờ nữa nó sẽ ở vị trí nào trên mặt biển. Từ đó mà ta phải cho biết vận tốc của tàu thủy bằng cách dùng một mũi tên để xác định thêm hướng của chuyển động. Vectơ từ đó được định nghĩa.

- Bản chất của vấn đề

+ Với hai điểm xác định A, B thì ta xác định được đoạn thẳng AB (hay là đoạn thẳng BA).

Nếu thêm dấu “ ” vào điểm B thì ta có vectơ với điểm đầu là A và điểm cuối là B (kí hiệu: AB ).

Tương tự: Nếu thêm dấu “ ” vào điểm A thì ta có vectơ với điểm đầu là B và

điểm cuối là A (kí hiệu: BA ).

Như vậy ta có: