Công thức biến đổi.
x' x
y' y
z' z
Ma trận biến đổi
1 0
0
1
T =
0 0
0
0
0 0
0
0
1 0
1
0
b. Đối xứng qua mặt phẳng xOz.
Là phép biến đổi mà giá trị của x và z trong vector vị trí không thay đổi.
Giá trị của y = -y.
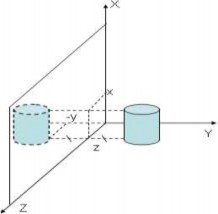
Hình 5.16 Đối xứng qua mặt phẳng xOz
Công thức biến đổi.
x' x
y' y
z' z
Ma trận biến đổi
1 0 0 0
T =
0
0
1 0
0 0 1 0
0
1
0
0
c. Đối xứng qua mặt phẳng yOz.
Là phép biến đổi mà giá trị của y và z trong vector vị trí là không thay đổi. Giá trị của x = -x
Hình 5.17 Đối xứng qua mặt phẳng zOy
Công thức biến đổi.
x' x
y' y
z' z
Ma trận biến đổi.
1 0 0 0
T =
0
0
1 0
0 0 1 0
0
1
0 0
d. Đối xứng qua mặt phẳng song với mặt phẳng gốc.
Để thực hiện phép đối xứng đối tượng qua một mặt phẳng song với mặt phẳng gốc ta thực hiện các bước sau:
Bước 1: Tịnh tiến đối tượng sao cho mặt phẳng đối xứng trùng với mặt phẳng
tọa độ.
Bước 2 : Thực hiện phép đối xứng qua mặt phẳng tọa độ. Bước 3 : Tịnh tiến về vị trí ban đầu.
Ví dụ: Đối xứng với mặt phẳng song song với mặt phẳng xOy. Bước 1: Dịch chuyển đối tượng sang hệ tọa độ tạm thời O‘x‘y‘z‘. Với O‘z‘ cách Oz một khoảng là dz.
1 0 0 0
0
0 1 0
0
Ma trận biến đổiT1 = 0 1 0
0
1
0 dz
Bước 2 : Thực hiện phép đối xứng qua mặt phẳng x‘O‘y‘.
1 0
0 1
0
Ma trận biến đổiT2 = 0
0
0
0 0
0
0
1 0
1
0
Bước 3 : Quay lại vị trí ban đầu.
1 0
0 1
0
Ma trận biến đổiT = 0
0
0
0 0
0
0
1 0
1
dz
→ [ T ] = [ T1 ]* [ T2 ]* [ T3 ]
1 0
0 1
0 01 0
0 00 1
0 0
0 0
1 0 0 0
0 1 0 0
[T] = * *
0 0
0
0
1 0
0 1
0
[T] = 0
0
0
1
dz
0
0
1
dz2
00 0
1
0
0
0
0
0
1
1 0
1
0
0 0
0
0
1 0
1
dz
e. Đối xứng với mặt phẳng song song với mặt phẳng xOz.
Bước 1: Dịch chuyển đối tượng sang hệ tọa độ tạm thời O‘x‘y‘z‘. Với O‘y‘ cách Oy một khoảng là dy.
1 0
0
0
0
Ma trận biến đổi[T1] = 1
0
dy
0 0
0
0
1 0
1
0
Bước 2 : Thực hiện phép đối xứng qua mặt phẳng x‘O‘z‘.
1
0
0
Ma trận biến đổi[T2] =
0
0 0 0
0
1 0
0 1 0
1
0 0
Bước 3 : Quay lại vị trí ban đầu.
1
0
0
Ma trận biến đổi[T3] =
0
0
1
0
dy
0 0
0
0
1 0
1
0
→ [ T ] = [ T1 ]* [ T2 ]* [ T3 ]
1 0
0 1
0 01
0 00
0 0
1 0
01 0
00 1
0 0
0 0
[T] =
* *
0
0
1
0
[T] =
0
0
0
dy
0
1
0
dy2
1 00
1
0
0
0 0
0
0
1 0
1
0
0 1 00
1
0
0 0
0
dy
1 0
1
0
f. Đối xứng với mặt phẳng song song với mặt phẳng yOz.
Bước 1: Dịch chuyển đối tượng sang hệ tọa độ tạm thời O‘x‘y‘z‘. Với O‘x‘ cách Ox một khoảng là dx.
1
0
0
Ma trận biến đổi[T1] =
dx
0 0 0
0
1 0
0 1 0
1
0 0
Bước 2 : Thực hiện phép đối xứng qua mặt phẳng y‘O‘z‘.
1 0 0 0
0
0 1 0
0
Ma trận biến đổi[T2] = 0 1 0
0
1
0 0
Bước 3 : Quay lại vị trí ban đầu.
1
0
Ma trận biến đổi[T3] = 0
0 0 0
0
1 0
0 1 0
1
dx 0 0
→ [ T ] = [ T1 ]* [ T2 ]* [ T3 ]
1 0 0
0 1 0
01 0 0
0 0 1 0
01
00
0 0 0
1 0 0
[T] =
* *
0 0 1
0 0 0 1 0 0 0 1 0
dx
0
1
1
0
0 0
0 0 0
1
0 0
dx
1
0 0
0
[T] = 0
1 0
0 1 0
2
dx
1
0 0
5.3.6 Kết hợp các phép biến đổi affine ba chiều
Để kết hợp các phép biến đổi affine ba chiều, chúng ta cũng thực hiện tương tự như ở phép biến đổi hai chiều bằng cách dùng hệ tọa độ thuần nhất.
Bằng cách này chúng ta cũng có các kết quả tương tự như trong trường hợp biến đổi hai chiều. Nếu M1 biến đổi P thành Q và M2 biến đổi Q thành S thì M1M2 sẽ biến đổi P thành S, do đó ma trận kết hợp của nhiều phép biến đổi có thể được tính từ việc nhân các ma trận của các phép biến đổi thành phần.
5.4. Các phép chiếu của vật thể trong không gian lên mặt phẳng
5.4.1. Định nghĩa chung
Đồ họa 3 chiều (3D computer graphics) bao gồm việc bổ sung kích thước về chiều sâu của đối tượng, cho phép biểu diễn chúng trong thế giới thực một cách chính xác và sinh động hơn.
Tuy nhiên các thiết bị truy xuất hiện tại đều là 2 chiều, do vậy việc biểu diễn được thực thi thông qua phép tô trát (render) để gây ảo giác (illusion) về độ sâu.
Đồ hoạ 3D là việc chuyển thế giới tự nhiên dưới dạng các mô hình biểu diễn trên các thiết bị hiển thị thông qua kỹ thuật tô trát (rendering).
Định nghĩa phép chiếu: phép chiếu là phép chuyển đổi những điểm của đối tượng trong hệ thống tọa độ n chiều thành những điểm trong hệ thống tọa độ có số chiều nhỏ hơn n.
Định nghĩa hình chiếu: Ảnh của đối tượng trên mặt phẳng chiếu được hình thành từ phép chiếu bởi các đường thẳng gọi là tia chiếu (projector) xuất phát từ một điểm gọi là tâm chiếu (center of projection) đi qua các điểm của đối tượng giao với mặt chiếu (projection plan).
Các bước xây dựng hình chiếu
1. Đối tượng trong không gian 3D với tọa độ thực được cắt theo một không gian xác định gọi là view volume.
2. View volume được chiếu lên mặt phẳng chiếu. Diện tích choán bởi view volume trên mặt phẳng chiếu đó sẽ cho ta khung nhìn.
3. Ánh xạ khung nhìn vào trong một cổng nhìn bất kỳcho trước trên màn hình để hiển thị hình ảnh.
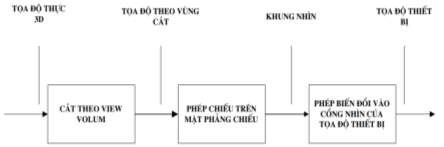
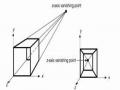
Hình 5.15. Mô hình nguyên lý của tiến trình biểu diễn
5.4.2. Phân loại phép chiếu
Các phép chiếu hình học phẳng được xây dựng trên cơ sở của 2 phép chiếu cơ bản là phép chiếu song song và phép chiếu phối cảnh. Sự khác biệt của hai phép chiếu là vị trí của tâm chiếu. Khi khoảng cách giữa tâm chiếu và mặt phẳng chiếu là hữu hạn thì phép chiếu đó được gọi là phép chiếu phối cảnh. Khi khoảng cách giữa tâm chiếu
và mặt phẳng chiếu là vô hạn thì các tia chiếu được coi như song song với nhau và phép chiếu được gọi là phép chiếu song song.
Việc phát triển của các phép biến đổi có 2 phương pháp được sử dụng:
- Thứ nhất: Khi tâm phép chiếu trùng với mắt người sử dụng là cố định và mặt phẳng chiếu vuông góc với hướng của mắt nhìn.
- Thứ hai: Khi đối tượng là cố định và tâm chiếu tự do dịch chuyển trong không gian 3D và mặt phẳng chiếu không nhất thiết vuông góc với hướng nhìn.
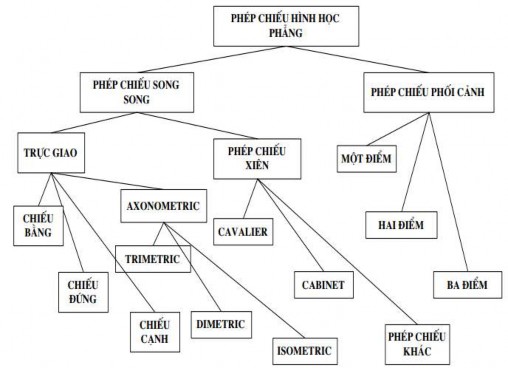
Hình 5.16. Phân loại phép chiếu
5.4.3. Phép chiếu song song
Phép chiếu song song (Parallel Projections) là phép chiếu mà ở đó các tia chiếu song song với nhau hay xuất phát từ điểm vô cùng.
Phân loại phép chiếu song song dựa trên hướng của tia chiếu (Direction Of Projection)và mặt phẳng chiếu (projection plane).
1) Phép chiếu trực giao (Orthographic projection)
Là phép chiếu song song và tia chiếu vuông góc với mặt phẳng chiếu. Về mặt toán học, phép chiếu trực giao là phép chiếu với một trong các mặt phẳng toạ độcó giá trị bằng 0. Thường dùng mặt phẳng z = 0, ngoài ra x=0 và y=0.
Ứng với mỗi mặt phẳng chiếu ta có một ma trận chiếu tương ứng.
1 0 0 0
0 0 0 0
1 0 0 0
0 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 |
0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 |
Có thể bạn quan tâm!
-
 Đồ họa máy tính - 16
Đồ họa máy tính - 16 -
 Vật Thể Ba Chiều Được Biểu Diễn Bằng Mô Hình Khung Nối Kết
Vật Thể Ba Chiều Được Biểu Diễn Bằng Mô Hình Khung Nối Kết -
 Phép Biến Dạng Theo Trục X: A = B = 1, Các Hệ Số Khác Bằng 0
Phép Biến Dạng Theo Trục X: A = B = 1, Các Hệ Số Khác Bằng 0 -
 Ảnh Của Phép Chiếu Trimetric Với Các Tham Số Góc Xoay Thay Đổi
Ảnh Của Phép Chiếu Trimetric Với Các Tham Số Góc Xoay Thay Đổi -
 Phép Biến Đổi Mô Hình Và Phép Biến Đổi Hệ Trục Toạ Độ
Phép Biến Đổi Mô Hình Và Phép Biến Đổi Hệ Trục Toạ Độ -
 Đồ họa máy tính - 22
Đồ họa máy tính - 22
Xem toàn bộ 240 trang tài liệu này.
[Ty]= 0 0 0 0[Tx]= 0 1 0 0[Tz]= 0 1 0 0
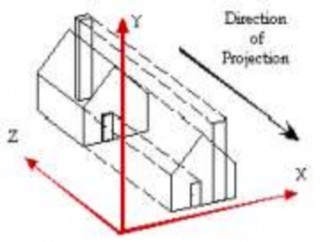
Hình 5.18 Phép chiếu trực giao
Thông thường thì người ta không sử dụng cả 6 mặt phẳng để suy diễn ngược hình của một đối tượng mà chỉ sử dụng một trong số chúng như: hình chiếu bằng, đứng, cạnh.
Cả sáu góc nhìn đều có thể thu được từ một mặt phẳng chiếu thông qua các phép biến đổi hình học như quay, dịch chuyển hay lấy đối xứng.
Ví dụ: giả sử chúng ta có hình chiếu bằng trên mặt phẳng z=0, với phép quay đối tượng quanh trục một góc 90o sẽ cho ta hình chiếu cạnh.
Đối với các đối tượng mà các mặt của chúng không song song với một trong các mặt phẳng hệ toạ độ thì phép chiếu này không cho hình dạng thật của vật thể. Muốn nhìn vật thể chính xác hơn người ta phải hình thành phép chiếu thông qua việc quay và dịch chuyển đối tượng sao cho mặt phẳng đó song song với các trục toạ độ.