1
Bước 4: Ma trận của phép đối xứng qua đường thẳng y= -x + a được thực hiện bởi tích của 3 phép biến đổi sau:
T=T1*T2*T3
0 | 0 0 | 1 | 0 1 | 0 | 0 | |
= 0 | 1 | 0 ∗ 1 | 0 | 0 ∗ 0 | 1 | 0 |
0 | 𝑎 | 1 0 | 0 | 1 0 | −𝑎 | 1 |
Có thể bạn quan tâm!
-
Phương Pháp Biểu Diễn Đối Tượng Trong Không Gian Hai Chiều -
Phép Quay Quanh Tâm Là Điểm Bất Kì. (A) Đối Tượng Trước Khi Biến Đổi,(B) Sau Khi Tịnh Tiến Về Gốc Tọa Độ, (C) Sau Khi Quay Góc Α, (D) Sau Khi Tịnh -
Xây Dựng Công Thức Biến Đổi Đối Tượng Khi Thực Hiện Các Phép Biến Đổi: -
Vật Thể Ba Chiều Được Biểu Diễn Bằng Mô Hình Khung Nối Kết -
Phép Biến Dạng Theo Trục X: A = B = 1, Các Hệ Số Khác Bằng 0 -
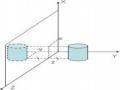
Các Phép Chiếu Của Vật Thể Trong Không Gian Lên Mặt Phẳng
Xem toàn bộ 240 trang tài liệu này.
1 | 0 | |
= 1 | 0 | 0 |
𝑎 | −𝑎 | 1 |
2.
a. Xây dựng công thức biến đổi khi kết hợp phép tỉ lệ với hệ số (Sx, Sy) và phép quay một góc α quanh gốc tọa độ
𝑆𝑥 | 0 | 0 | |
Ma trận biến đổi T1= 0 | 𝑆𝑦 | 0 | |
0 | 0 | 1 | |
2: Phép quay với góc 𝛼 có ma trận là | |||
cos 𝛼 | sin 𝛼 | 0 | |
Ma trận biến đổi T2= − sin 𝛼 | cos 𝛼 | 0 | |
0 | 0 | 1 | |
Bước 1: Phép tỉ lệ với hệ số tỉ lệ (Sx, Sy)
Bước
Bước 3: Ma trận của kết hợp phép tỉ lệ với hệ số (Sx, Sy) và phép quay một góc α quanh gốc tọa độ là
T=T1*T2
𝑆𝑥 0 0
cos 𝛼 sin 𝛼 0
= 0 𝑆𝑦 0 ∗ − sin 𝛼 cos 𝛼 0
0 0 1
0 0 1
𝑆𝑥 ∗ sin 𝛼 | 0 | |
= −𝑆𝑦 ∗ sin 𝛼 | 𝑆𝑦 ∗ cos 𝛼 | 0 |
0 | 0 | 1 |
b. Xây dựng công thức biến đổi khi kết hợp phép tỉ lệ với hệ số (Sx, Sy) giữ nguyên điểm chốt (x0, y0) và phép quay một góc α quanh (x0, y0)
Bước 1: Tịnh tiến điểm chốt (x0, y0) về gốc tọa độ
1 0 0
Ma trận biến đổi :T1=
0 1 0
−𝑥0 −𝑦0 1
Bước 2: Phép tỉ lệ với hệ số tỉ lệ (Sx, Sy)
0 | 0 | |
Ma trận biến đổi :T2= 0 | 𝑆𝑦 | 0 |
0 | 0 | 1 |
Bước 3: Phép quay với góc 𝛼 quanh gốc tọa độ
sin 𝛼 | 0 | |
Ma trận biến đổi T3= − sin 𝛼 | cos 𝛼 | 0 |
0 | 0 | 1 |
Bước 4: Phép tịnh tiến điểm (x0, y0) về vị trí ban đầu
0 | 0 | |
Ma trận biến đổi T4= 0 | 1 | 0 |
𝑥0 | 𝑦0 | 1 |
Bước 5: Ma trận của phép tỉ lệ với hệ số tỉ lệ (Sx, Sy) và phép quay một góc α quanh gốc tọa độ được thực hiện bởi tích của 4 phép biến đổi sau:
T=T1*T2*T3*T4
1 0 0
𝑆𝑥 0 0
cos 𝛼 sin 𝛼 0
1 0 0
= 0 1 0 ∗ 0 𝑆𝑦 0 ∗ − sin 𝛼 cos 𝛼 0 ∗ 0 1 0
−𝑥0 −𝑦0 1
0 0 1
0 0 1
𝑥0 𝑦0 1
=
𝑆𝑥 ∗ cos 𝛼 𝑆𝑥 ∗ sin 𝛼 0
−𝑆𝑦 ∗ sin 𝛼 𝑆𝑦 ∗ cos 𝛼 0
𝑥0 ∗ (1 − 𝑆𝑥 ∗ cos 𝛼) + 𝑦0 ∗ 𝑆𝑦 ∗ sin 𝛼 𝑦0 ∗ (1 − 𝑆𝑦 ∗ cos 𝛼) − 𝑥0 ∗ 𝑆𝑥 ∗ sin 𝛼 1
3.Xây dựng ma trận biến đổi
Tịnh tiến điểm (x0, y0) về gốc tọa độ :
1 0 0
Ma trận biến đổi T1=
0 1 0
−𝑥0 −𝑦0 1
Thực hiện phép tỉ lệ với hệ số (Sx, Sy):
0 | 0 | ||
Ma trận biến đổi T2= 0 | 𝑆𝑦 | 0 | |
0 | 0 | 1 | |
Thực hiện phép quay với góc 𝛼 | : | ||
cos 𝛼 | sin 𝛼 | 0 | |
Ma trận biến đổi T3= − sin 𝛼 | cos 𝛼 | 0 | |
0 | 0 | 1 | |
𝑆𝑥
Tịnh tiến về vị trí ban đầu:
1 0 0
Ma trận biến đổi T4= 0 1 0
𝑥0 𝑦0 1
Ma trận tổng hợp
T=T1*T2*T3*T4
1 0 0
𝑆𝑥 0 0
cos 𝛼 sin 𝛼 0
1 0 0
= 0 1 0 ∗ 0 𝑆𝑦 0 ∗ − sin 𝛼 cos 𝛼 0 ∗ 0 1 0
−𝑥0 −𝑦0 1
Kết quả T =
0 0 1
0 0 1
𝑥0 𝑦0 1
𝑆𝑥 ∗ cos 𝛼 𝑆𝑥 ∗ sin 𝛼 0
−𝑆𝑦 ∗ sin 𝛼 𝑆𝑦 ∗ cos 𝛼 0
𝑥0 ∗ (1 − 𝑆𝑥 ∗ cos 𝛼) + 𝑦0 ∗ 𝑆𝑦 ∗ sin 𝛼 𝑦0 ∗ (1 − 𝑆𝑦 ∗ cos 𝛼) − 𝑥0 ∗ 𝑆𝑥 ∗ sin 𝛼 1
4.
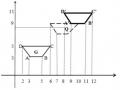
A(20, 10) => x‘A
= 20+52= 23.53553, y‘
A
2
= 20 - 52= 16.46447
2
B(10, 30) => x‘B = 20-5 2 = 12.92893, y‘B = 20
C(30,20) => x‘C
= 20+52= 23.53553, y‘
C
2
= 20 + 52= 23.53553
2
5. Xây dựng ma trận biến đổi
- Tịnh tiến điểm (x0, y0) về gốc tọa độ:
1 0 0
Ma trận biến đổi T1=
0 1 0
−𝑥0 −𝑦0 1
Thực hiện phép quay với góc 𝛼 :
sin 𝛼 | 0 | |
Ma trận biến đổi T2= − sin 𝛼 | cos 𝛼 | 0 |
0 | 0 | 1 |
Thực hiện phép tỉ lệ với hệ số (Sx, Sy):
0 | 0 | |
Ma trận biến đổi T3= 0 | 𝑆𝑦 | 0 |
0 | 0 | 1 |
Tịnh tiến về vị trí ban đầu:
1 0 0
Ma trận biến đổi T4= 0 1 0
𝑥0 𝑦0 1
Ma trận tổng hợp
T=T1*T2*T3*T4
0 | 0 | cos 𝛼 | sin 𝛼 | 0 𝑆𝑥 | 0 | 0 1 | 0 | 0 | |
= 0 | 1 | 0 ∗ | − sin 𝛼 | cos 𝛼 | 0 ∗ 0 | 𝑆𝑦 | 0 ∗ 0 | 1 | 0 |
−𝑥0 Kết quả | −𝑦0 | 1 | 0 | 0 | 1 0 | 0 | 1 𝑥0 | 𝑦0 | 1 |
𝑆𝑥 ∗ cos 𝛼 𝑆𝑦 ∗ sin 𝛼 0
−𝑆𝑥 ∗ sin 𝛼 𝑆𝑦 ∗ cos 𝛼 0
𝑥0 ∗ (1 − 𝑆𝑥 ∗ cos 𝛼) + 𝑦0 ∗ 𝑆𝑥 ∗ sin 𝛼 𝑦0 ∗ (1 − 𝑆𝑦 ∗ cos 𝛼) − 𝑥0 ∗ 𝑆𝑦 ∗ sin 𝛼 1
6.
A(5,0) => x‘A = 25 - 10 3 = 7.679491, y‘A = -5 - 10 3 = -17.32051 B(10, 10) => x‘B = 15 - 5 3 = 6.339745, y‘B = -5
C(30,20) => x‘C = 5 + 15 3 = 30.98076, y‘C = 25 + 10 3 = 42.32051
7. Xây dựng ma trận biến đổi
Tịnh tiến điểm (x0, y0) về gốc tọa độ :
1 0 0
Ma trận biến đổi T1=
0 1 0
−𝑥0 −𝑦0 1
Thực hiện phép tỉ lệ với hệ số (Sx, Sy):
0 | 0 | |
Ma trận biến đổi T2= 0 | 𝑆𝑦 | 0 |
0 | 0 | 1 |
Thực hiện lấy đối xứng qua gốc tọa độ
−1 0 0
Ma trận biến đổi T3 = 0 −1 0
0 0 1
Tịnh tiến về vị trí ban đầu:
0 | 0 | |
Ma trận biến đổi T4= 0 | 1 | 0 |
𝑥0 | 𝑦0 | 1 |
1
Ma trận tổng hợp T=T1*T2*T3*T4
0 | 0 𝑆𝑥 | 0 | 0 | −1 | 0 | 0 1 | 0 | 0 | |
= 0 | 1 | 0 ∗ 0 | 𝑆𝑦 | 0 ∗ | 0 | −1 | 0 ∗ 0 | 1 | 0 |
−𝑥0 Kết quả | −𝑦0 | 1 0 | 0 | 1 | 0 | 0 | 1 𝑥0 | 𝑦0 | 1 |
T =
−𝑆𝑥 0 0
0 −𝑆𝑦 0
𝑥0 ∗ (1 + 𝑆𝑥 ) 𝑦0 ∗ (1 + 𝑆𝑦 ) 1
8. Tọa độ điểm A không đổi sau khi thực hiện phép biến đổi B(5, 5) => xB = -10, yB = 20
C(10,30) => xC = -20, yC = -30
9.Xây dựng ma trận biến đổi
Tịnh tiến sao cho đường thẳng y = x+a trùng với đường thẳng y = x (tịnh tiến điểm (-a, 0) về gốc tọa độ ):
0 | 0 | |
Ma trận biến đổi T1= 0 | 1 | 0 |
𝑎 | 0 | 1 |
Thực hiện lấy đối xứng qua đường thẳng y = x
1 | 0 | |
Ma trận biến đổi T2 = 1 | 0 | 0 |
0 | 0 | 1 |
Tịnh tiến về vị trí ban đầu: Ma trận biến đổi T3=
1 0 0
0 1 0
−𝑎 0 1
Thực hiện phép tỉ lệ với hệ số (Sx, Sy):
0 | 0 | |
Ma trận biến đổi T4= 0 | 𝑆𝑦 | 0 |
0 | 0 | 1 |
Ma trận tổng hợp T=T1*T2*T3*T4
0 | 0 0 | 1 0 | 1 | 0 | 0 𝑆𝑥 | 0 | 0 | |
= 0 | 1 | 0 * 1 | 0 0 * | 0 | 1 | 0 ∗ 0 | 𝑆𝑦 | 0 |
𝑎 | 0 | 1 0 | 0 1 | −𝑎 | 0 | 1 0 | 0 | 1 |
Kết quả
0 𝑆𝑦 0
𝑆𝑥 0 0
−𝑎 ∗ 𝑆𝑥 𝑎 ∗ 𝑆𝑦 1
10.A(0,0) => xA = -10, yA = 10 B(10, 5) => xB = 0, yB = 30
C(5, 20) => xC = 30, yB = 20
11.Xây dựng ma trận biến đổi
Tịnh tiến điểm (x0, y0) về gốc tọa độ :
1 0 0
Ma trận biến đổi T1=
0 1 0
−𝑥0 −𝑦0 1
Thực hiện phép quay với góc 𝛼 :
sin 𝛼 | 0 | |
Ma trận biến đổi T2= − sin 𝛼 | cos 𝛼 | 0 |
0 | 0 | 1 |
Thực hiện lấy đối xứng qua trục hoành
0 | 0 | |
Ma trận biến đổi T3= 0 | −1 | 0 |
0 | 0 | 1 |
Tịnh tiến về vị trí ban đầu :
1 0 0
Ma trận biến đổi T4= 0 1 0
𝑥0 𝑦0 1
Ma trận tổng hợp T=T1*T2*T3*T4
1 | 0 | 0 cos 𝛼 | sin 𝛼 | 0 1 | 0 | 0 1 | 0 | 0 | |
= | 0 | 1 | 0 ∗ − sin 𝛼 | cos 𝛼 | 0 * 0 | −1 | 0 * 0 | 1 | 0 |
−𝑥0 | −𝑦0 | 1 0 | 0 | 1 0 | 0 | 1 𝑥0 | 𝑦0 | 1 | |
Kết quả |
T =
𝑐𝑜𝑠𝛼 −𝑠𝑖𝑛𝛼 0
−𝑠𝑖𝑛𝛼 −𝑐𝑜𝑠𝛼 0
𝑦0 ∗ 𝑠𝑖𝑛𝛼 + 𝑥0(1 − 𝑐𝑜𝑠𝛼) 𝑥0 ∗ 𝑠𝑖𝑛𝛼 + 𝑦0 (1 + 𝑐𝑜𝑠𝛼) 1
12.A(0, 0) => A‘(5( 3 +1)/2, 5( 3 +3)/2) = (6.830127, 11.83013)
B(10, 10) => B‘((15 -5 3 )/2, (5 -5 3 )/2) = (3.169873, -1.830127)
C(5, 20) => C‘((10 -15 3 )/2, -5/2) = (-7.990381, -2.5)
13. Xây dựng ma trận biến đổi
Tịnh tiến sao cho đường thẳng y = -x+a trùng với đường thẳng y = -x (tịnh tiến điểm (-a, 0) về gốc tọa độ ):
Ma trận biến đổi T1=
1 0 0
0 1 0
−𝑎 0 1
Thực hiện lấy đối xứng qua đường thẳng y = -x
−1 | 0 | |
Ma trận biến đổi T2 = −1 | 0 | 0 |
0 | 0 | 1 |
Tịnh tiến về vị trí ban đầu:
1 0 0
Ma trận biến đổi T3= 0 1 0
𝑎 0 1
Thực hiện phép tỉ lệ với hệ số (Sx, Sy):
0 | 0 | |
Ma trận biến đổi T4= 0 | 𝑆𝑦 | 0 |
0 | 0 | 1 |
Ma trận tổng hợp
T=T1*T2*T3*T4
1 | 0 | 0 0 | −1 | 0 1 | 0 | 0 𝑆𝑥 | 0 | 0 | |
= | 0 | 1 | 0 * −1 | 0 | 0 * 0 | 1 | 0 ∗ 0 | 𝑆𝑦 | 0 |
−𝑎 | 0 | 1 0 | 0 | 1 𝑎 | 0 | 1 0 | 0 | 1 | |
Kết quả |
T =
0 −𝑆𝑦 0
−𝑆𝑥 0 0
𝑎 ∗ 𝑆𝑥 𝑎 ∗ 𝑆𝑦 1
14. A(0,0) => xA = 15, yA = 15
B(10, 5) => xB = 0, yB = -15
C(5, 20) => xC = -45, yB = 0
Chương 5
CÁC PHÉP BIẾN ĐỔI HÌNH HỌC 3 CHIỀU
5.1. Giới thiệu đồ họa ba chiều
Các đối tượng trong thế giới thực phần lớn là các đối tượng ba chiều, nên việc thể hiện các đối tượng ba chiều trên máy tính là một công việc hết sức cần thiết để đưa tin học gần gũi với thực tế hơn. Cũng giống như các cách biểu diễn các đối tượng ba chiều trên mặt phẳng khác (như của máy ảnh, camera, ... ), biểu diễn bằng máy tính cũng phải tuân theo các quy luật về phối cảnh, sáng, tối, ... nhằm giúp người xem có thể tưởng tượng lại hình ảnh một cách gần đúng nhất. Ngoài ra biểu diễn trên máy tính có ưu thế giúp ta có thể quan sát đối tượng ở nhiều góc cạnh khác nhau, ở các khoảng cách khác nhau.
5.1.1. Tổng quan về đồ họa ba chiều
Khi mô hình hóa và hiển thị một cảnh ba chiều, cần phải xem xét rất nhiều khía cạnh và vấn đề khác nhau chứ không đơn giản là thêm vào tọa độ thứ ba cho các đối tượng. Bề mặt đối tượng có thể xây dựng bởi nhiều tổ hợp khác nhau của các mặt phẳng và các mặt cong. Ngoài ra, đôi khi cũng cần mô tả một số thông tin bên trong các đối tượng. Các công cụ hỗ trợ đồ họa (graphics package) thường cung cấp một số hàm hiển thị các thành phần bên trong, những đường nét tiêu biểu hoặc hiển thị một phần của đối tượng ba chiều (solid object). Ngoài ra, các phép biến đổi hình học thường được sử dụng nhiều hơn và đa dạng hơn trong đồ họa ba chiều so với trong đồ họa hai chiều. Phép biến đổi hệ quan sát trong không gian ba chiều phức tạp hơn nhiều so với trong không gian hai chiều do ta phải chọn lựa nhiều tham số hơn khi mô tả một cảnh ba chiều sẽ xuất hiện trên màn hình như thế nào.
Hình 5.1 Một cảnh đồ họa ba chiều