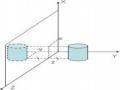
20. Hình sau là phép chiếu:
[a]--Dimetric [b]--Trimetric
[c]--Othergraphic (trực giao) [d]—Isometric
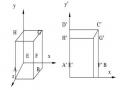
21. Hình sau là phép chiếu:
[a]--Othergraphic (trực giao) [b]--Isometric
[c]--Trimetric [d]--Dimetric
22. Hình sau là phép chiếu:
[a]--Cavalier
[b]--Phối cảnh một tâm chiếu [c]--Cabinet
[d]--Phối cảnh hai tâm chiếu
23. Hình sau là phép chiếu:
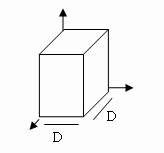
[a]--Phối cảnh một tâm chiếu [b]--Cavalier
[c]--Phối cảnh hai tâm chiếu [d]—Cabinet
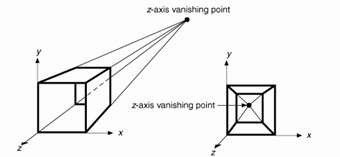
24. Hình sau là phép chiếu:
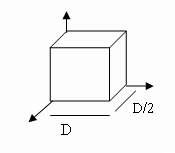
[a]--Phối cảnh một tâm chiếu [b]--Cavalier
[c]--Cabinet
[d]--Phối cảnh hai tâm chiếu
25. Hình sau là phép chiếu:
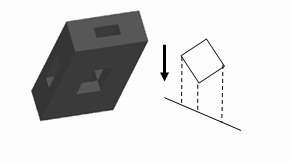
[a]--Phối cảnh
[b]--Xiên
[c]--Trực giao
[d]--Trục lượng
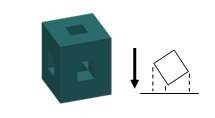
26. Hình sau là phép chiếu:
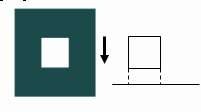
[a]--Xiên
[b]--Phối cảnh
[c]--Trực giao [d]--Trục lượng
27. Các phép sau phép nào không phải phép chiếu phối cảnh: [a]--Một tâm chiếu
[b]--Ba tâm chiếu [c]--Hai tâm chiếu [d]--Bốn tâm chiếu
28. Trường hợp φ = 45o và quang cảnh đạt được gọi là :
[a]--Phép chiếu isometric projection [b]--Phép chiếu cabinet
[c]--Phép chiếu cavalier
[d]--Phép chiếu axonometric orthographic projection
29. Trong phép chiếu cavalier, tất cả các đường vuông góc với mặt phẳng chiếu được chiếu với chiều dài:
[a]--Ngắn hơn 1/2 chiều dài ban đầu [b]--Dài hơn 1/2 chiều dài ban đầu
[c]--Tỉ lệ phụ thuộc vào chiều dài của vật được chiếu [d]--Chiều dài không thay đổi.
30. Khi góc chiếu được chọn để tgφ = 2, kết quả quang cảnh được gọi là : [a]--Phép chiếu isometric projection
[b]--Phép chiếu cabinet [c]--Phép chiếu cavalier
[d]--Phép chiếu axonometric orthographic projection
Bài tập
1. Trong không gian Oxyz cho 2 điểm A(2, 3, 5); B(2, 0, 5) xác định công thức biến đổi của 1 điểm sau khi quay quanh AB một góc 90o sau đó quay quanh trục Ox một góc -90o
2. Xây dựng công thức biến đổi đối tượng khi thực hiện phép tỉ lệ với hệ số tỉ lệ (Sx, Sy, Sz) giữ nguyên điểm chốt (x0, y0, z0)
3. Xây dựng công thức biến đổi đối tượng sau khi thực hiện phép đối xứng qua điểm có tọa độ (x0, y0, z0)
4. Xây dựng công thức biến đổi đối tượng sau khi thực hiện phép đối xứng qua trục song song với trục Ox, cách trục Oy, Oz một khoảng ty, tz
5. Xây dựng công thức biến đổi đối tượng sau khi thực hiện phép đối xứng qua mặt phẳng song song với mặt phẳng xOy, cách mặt phẳng xOy một khoảng tz
6. Xây dựng công thức biến đổi đối tượng khi quay đối tượng một góc α quanh trục Oy rồi quay một góc β quanh trục Oz
7. Xây dựng công thức biến đổi đối tượng sau khi tịnh tiến đối tượng theo vector tịnh tiến (tx, ty, tz) rồi quay quanh trục Ox một góc α sau đó quay quanh trục Oy một góc β.
8. Cho đoạn thẳng AB với điểm A(0, 0 , 0), B(0, 10, 5). Hãy xác định tọa độ mới của đoạn thẳng AB sau khi thực hiện quay một góc 300 quanh trục Oy và phép quay một góc 450 quanh trục Oz.
9. Xây dựng công thức biến đổi đối tượng trong không gian sau khi quay đối tượng một góc α quanh trục song song với trục Ox, cách trục Oy, Oz một khoảng ty, tz.
10. Cho đoạn thẳng AB với điểm A(0, 0 , 0), B(10, 0, 1). Hãy xác định tọa độ mới của đoạn thẳng AB sau khi quay đoạn thẳng một góc 300 quanh trục song song với trục Ox, cách trục Oy, Oz một khoảng ty = 5, tz = 10.
11. Cho hình hộp chữ nhật ABCDEFGH với các tọa độ A(0,0,1), B(5,0,1), C(5,3,1), D(0,3,1), E(0,0,0), F(5,0,0), G(5,3,0), H(0,3,0)
a. Tìm ma trận tỉ lệ để chuyển hình hộp đã cho thành hình hộp đơn vị
b. Xây dựng phép chuyển đổi hình hộp qua phép quay 1 góc -900 quanh trục z rồi quay 450 quanh trục y
12. Cho hình hộp chữ nhật ABCDEFGH với các tọa độ A(0,0,1), B(5,0,1), C(5,3,1), D(0,3,1), E(0,0,0), F(5,0,0), G(5,3,0), H(0,3,0). Tìm ma trận biến đổi khi quay hình hộp một góc 450 quanh trục đi qua trọng tâm hình hộp và song song với trục Oy.
13.
a. Xây dựng công thức biến đổi của đối tượng trong không gian sau khi thực hiện phép tỉ lệ với hệ số (Sx, Sy, Sy) sao cho điểm chốt (x0, y0, z0) không đổi.
b. Cho hình hộp chữ nhật ABCDEFGH với các tọa độ A(0,0,1), B(5,0,1), C(5,3,1), D(0,3,1), E(0,0,0), F(5,0,0), G(5,3,0), H(0,3,0). Xác định tọa độ mới của hình hộp sau khi thu nhỏ bằng 1/2 kích thước ban đầu sao cho tọa độ trọng tâm hình hộp không đổi.
14.
a. Trong không gian 3 chiều Oxyz cho điểm Q(x,y,z). Xây dựng công thức biến đổi của điểm sau khi dịch chuyển điểm đó một khoảng tz theo trục Oz rồi quay 1 góc ỏ quanh trục Oz rồi quay một góc ò quanh trục Oy
b. Áp dụng với điểm Q(10,10,0), α = -450, β= 900
Hướng dẫn giải bài tập
1.
Nhận xét rằng đoạn AB song song với trục Oy trong hệ tọa độ Oxyz, cách Ox một khoảng là dx = 5, cách Oz một khoảng là dz = 2.
Đưa phép biến đổi về dạng: quay đối tượng quanh trục song song với trục tọa độ Ox một góc 900, sau đó quay quanh trục Ox một góc -900
Bước 1: Tịnh tiến đối tượng để AB trùng với trục Ox với vector tịnh tiến (-5, 0,
-2).
Bước 2: Quay quanh AB một góc 90o.
Bước 3: Tịnh tiến ngược về vị trí ban đầu
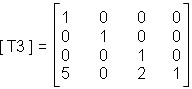
Bước 4: Quay đối tượng quanh trục Ox một góc -90o.
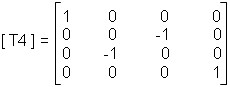
→ Ma trận biến đổi tổng hợp [ T ] = [ T1 ]* [ T2 ]* [ T3 ]* [ T4 ].
Công thức biến đổi: X‘ = X * M
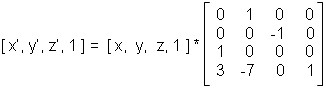
x' z 3
Công thức biến đổi y' x 7
z' z
2.
- Bước 1: Tịnh tiến điểm (x0, y0,z0) về gốc tọa độ có ma trận là:
1 0 0 0
T1=
0 1 0 0
0 0 1 0
−𝑥0 −𝑦0 −𝑧0 1
- Bước 2: Phép biến đổi tỉ lệ (Sx, Sy, Sz) có ma trận là
𝑆𝑥 0 0 0
0 | 0 | 𝑆𝑧 | 0 |
0 | 0 | 0 | 1 |
Có thể bạn quan tâm!
-
Các Phép Chiếu Của Vật Thể Trong Không Gian Lên Mặt Phẳng -
Ảnh Của Phép Chiếu Trimetric Với Các Tham Số Góc Xoay Thay Đổi -
Phép Biến Đổi Mô Hình Và Phép Biến Đổi Hệ Trục Toạ Độ -
Bảng So Sánh Khoảng Biến Động Của Các Thiết Bị Truy Xuất Đồ Họa -
Phân Bố Các Điểm Trong Vùng Theo Thứ Tự Tăng Dần -
Giới Thiệu Về Các Hệ Màu Trong Màn Hình Đồ Họa
Xem toàn bộ 240 trang tài liệu này.
T2= 0 𝑆𝑦 0 0
- Bước 3: Tịnh tiến ngược về vị trí ban đầu có ma trận là
1 0 0 0
3
T = 0 1 0 0
0 0 1 0
𝑥0 𝑦0 𝑧0 1
- Bước 4: Ma trận của phép tỉ lệ với hệ số tỉ lệ (Sx, Sy, Sz) giữ nguyên điểm chốt (x0, y0, z0)
T=T1*T2*T3
1 0 0 0
𝑆𝑥 0 0 0
1 0 0 0
= 0 1 0 0 ∗ 0 𝑆𝑦 0 0 ∗ 0 1 0 0
0 0 1 0
−𝑥0 −𝑦0 −𝑧0 1
0 0 𝑆𝑧 0
0 0 0 1
0 0 1 0
𝑥0 𝑦0 𝑧0 1
𝑆𝑥 | 0 | 0 | 0 |
0 | 𝑆𝑦 | 0 | 0 |
=0 0 𝑆𝑧 0
1 − 𝑆𝑥∗ 𝑥01 − 𝑆𝑦∗ 𝑦01 − 𝑆𝑧∗ 𝑧0 1
3.
- Bước 1: Tịnh tiến điểm (x0, y0,z0) về gốc tọa độ Ma trận biến đổi là:
1 0 0 0
T1=
0 1 0 0
0 0 1 0
−𝑥0 −𝑦0 −𝑧0 1
- Bước 2: Phép biến đổi đối xứng qua điểm qua gốc tọa độ Ma trận biến đổi là:
T2=
−1 | 0 | 0 | 0 |
0 | −1 | 0 | 0 |
0 0 −1 0
0 0 0 1
- Bước 3: Tịnh tiến ngược về vị trí ban đầu: Ma trận biến đổi là:
1 0 0 0
3
T = 0 1 0 0
0 0 1 0
𝑥0 𝑦0 𝑧0 1
- Bước 4: Ma trận của phép đối xứng qua điểm (x0, y0, z0) là T=T1*T2*T3
1 0 0 0
−1 0 0 0
1 0 0 0
= 0 1 0 0 ∗ 0 −1 0 0 ∗ 0 1 0 0
0 0 1 0 0 0 −1 0 0 0 1 0
−𝑥0 −𝑦0 −𝑧0 1 0 0 0 1 𝑥0 𝑦0 𝑧0 1
−1 0 0 0
= 0 −1 0 0
0 0 −1 0
2 ∗ 𝑥0 2 ∗ 𝑦0 2 ∗ 𝑧0 1
4.
1 | 0 | 0 | 0 |
0 | 1 | 0 | 0 |
0 | −𝑡𝑦 | −𝑡𝑧 | 1 |
- Bước 1: Tịnh tiến đối xứng về gốc tọa độ có ma trận là:
T1= 0 0 1 0
- Bước 2: Đối xứng qua trục Ox có ma trận là
1 0 0 0
0 | 0 | −1 | 0 |
0 | 0 | 0 | 1 |
T2= 0 −1 0 0
1 | 0 | 0 | 0 |
0 | 1 | 0 | 0 |
0 | 𝑡𝑦 | 𝑡𝑧 | 1 |
- Bước 3: Tịnh tiến ngược về vị trí ban đầu có ma trận là
T3= 0 0 1 0
- Bước 4: Ma trận của phép quay quanh trục song song với trục Ox cách trục Oy, Oz 1 khoảng ty,tz là