x' x trx
y' y try
z' z trz
Ma trận phép tịnh tiến có dạng như sau:
1
0 [T (trx, try, trz)]
0
trx
0
1
0
try
0 0
0
0
1 0
1
trz
5.3.2. Phép biến đổi tỉ lệ
Phép biến đổi tỉ lệ trong ba chiều là một sự mở rộng của phép biến đổi tỉ lệ trong hai chiều: Nếu thay đổi đối tượng một tỉ lệ sx theo trục Ox, sy theo trục Oy và sz theo trục Oz thì tọa độ của đối tượng biến đổi theo công thức:
x' x * Sx
y' y * Sy
z' z * Sz
Ma trận biến đổi:
Sx 0
0
Sy
S = 0 0
0
0
0 0
0
0
Sz 0
1
0
Trong đó các hằng số sx, sy, sz là các hệ số tỉ lệ tương ứng theo các trục x, y, z.
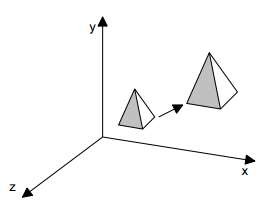
Hình 5.7. Phép biến đổi tỉ lệ
Chú ý.
Nếu sx = -1, sy = sz = 1 thì phép tỉ lệ là phép đối xứng qua mặt phẳng yOz. Nếu sy = -1, sx = sz = 1 thì phép tỉ lệ là phép đối xứng qua mặt phẳng xOz. Nếu sz = -1, sy = sx = 1 thì phép tỉ lệ là phép đối xứng qua mặt phẳng xOy. Nếu sx = sy = sz = 1 thì đối tượng được giữ nguyên hình dạng ban đầu.
Nếu 0 < sx, sy, sz < 1 thì phép biến đổi tương ứng là thu nhỏ đối tượng. Nếu sx, sy, sz > 1 thì phép biến đổi thu được là phép phóng to đối tượng. Khi các hệ số tỉ lệ sx, sy, sz bằng nhau, ta có phép biến đổi đồng dạng.
Trong phép biến đổi S(sx, sy, sz ), gốc tọa độ O sẽ có ảnh là chính nó. Ta gọi gốc tọa độ là điểm bất động (fixed point) của S, hay còn gọi O là tâm của phép biến đổi.
Tổng quát hơn, ta có thể mô tả một phép biến đổi tỉ lệ theo một tâm (xf, xf, xf) bất kì bằng một dãy ba phép biến đổi sau:
Tịnh tiến điểm bất động (xf, xf, xf) về gốc tọa độ. Thực hiện phép biến đổi tỉ lệ theo công thức
Tịnh tiến ngược điểm bất động từ gốc tọa độ trở về vị trí ban đầu.
Như vậy, kết hợp ba bước biến đổi trên ta có được ma trận biến đổi của phép biến đổi tỉ lệ theo tâm (xf, xf, xf)với hệ số tỉ lệ sx, sy, sz là:
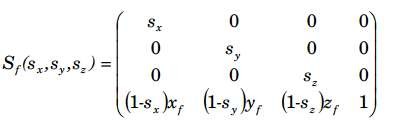
5.3.3. Phép biến dạng
Biến dạng theo bất kì trục tọa độ nào cũng bị ảnh hưởng bởi tọa độ ứng với hai trục còn lại. (Sự thay đổi của x phụ thuộc cả vào y và z và ngược lại.)
Công thức biến đổi.
x'x cy ez
y'ax y fz
z'bx dy z
Ma trận biến đổi.
1 a
c
e
f
Tsh = 1
0
0
b 0
0
d
1 0
1
0
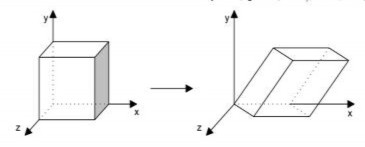
Hình 5.8. Phép biến dạng theo trục x: a = b = 1, các hệ số khác bằng 0
Tương tự như trong trường hợp phép biến đổi tỉ lệ, phép biến dạng Sh cũng có điểm bất động là gốc tọa độ O. Ta cũng có thể xây dựng phép biến dạng với tâm biến dạng tại một điểm (xf, xf, xf) bất kì.
Ma trận biến đổi của phép biến dạng với tâm tại (xf, xf, xf) là:
T =
f
y
1
c e
* c z f * e
x f
a
1
f
* a z f * f
x f
b d 1
* b y f * f
0
0
0
1
5.3.4. Phép quay
a. Phép quay quanh một trục tọa độ
Phép quay là phép biến đổi làm thay đổi hướng của đối tượng nhưng kích thước và hình dạng của đối tượng vẫn được giữ nguyên.
Khi quay đối tượng quanh một trục nào đó thì tọa độ của đối tượng tại trục đó sẽ không đổi.
Chiều dương của phép quay: Các định nghĩa về chiều quay được dùng chung cho cả hệ tọa độ theo quy ước bàn tay phải và bàn tay trái. Cụ thể chiều dương được định nghĩa như sau:
Quay quanh trục x: từ trục dương y đến trục dương z. Quay quanh trục y: từ trục dương z đến trục dương x.
Quay quanh trục z: từ trục dương x đến trục dương y.
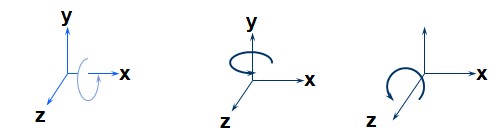
Hình 5.9 Cách xác định chiều quay dương
a. Quay đối tượng quanh trục Ox.
Là phép quay mà giá trị của x trong vector vị trí không thay đổi. Mặt phẳng xoay sẽ vuông góc với trục Ox.
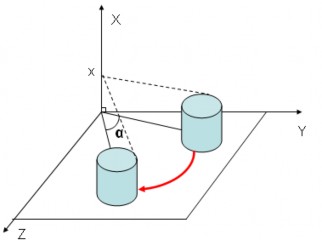
Hình 5.10 Quay đối tượng quanh trục Ox
Công thức biến đổi
x'x
y'y cosz sin
z'y sinz cos
Ma trận biến đổi.
1
0 [Tx]
0
0
0
cos
sin0
0 0
0
sin
cos0
1
0
b. Quay đối tượng quanh trục Oy.
Là phép quay mà giá trị của y trong vector vị trí không thay đổi. Mặt phẳng xoay sẽ vuông góc với trục Oy.
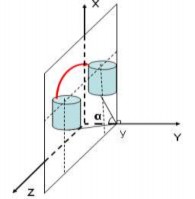
Hình 5.11 Quay đối tượng quanh trục Oy
Công thức biến đổi.
x'x cosz sin
y'y
z'x sinz cos
Ma trận biến đổi.
cos0 sin0
0
[Ty] 0 1 0
sin0 cos0
1
0
0
0
c. Quay đối tượng quanh trục Oz
Là phép quay mà giá trị của z trong vector vị trí không thay đổi. Mặt phẳng xoay sẽ vuông góc với trục Oz.
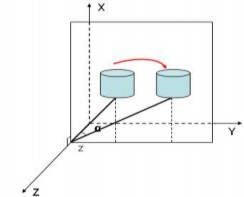
Hình 5.12 Quay đối tượng quanh trục Oz
Công thức biến đổi.
x'x cosy sin
y'x siny cos
z'z
Ma trận biến đổi.
cos
sin
[Tz]
sincos
0 0
0
0
0 0
0
0
1 0
1
0
b. Quay quanh một trục bất kỳ song song với các trục tọa độ.
Các ma trận biến đổi quay quanh các trục tọa độ rất có hiệu quả trong việc xử lý biến đổi các đối tượng, tuy nhiên việc quay các đối tượng thường dựa trên các trục song song với các trục tọa độ gốc. Quá trình quay đối tượng quanh các trục của chúng tuân thủ theo các bước sau:
Bước 1: Dịch chuyển đối tượng sao cho trục quay trùng với trục tọa độ
Bước 2 : Quay đối tượng quanh trục của nó (tương đương với trục tọa độ gốc). Bước 3 : Đưa trả đối tượng về vị trí ban đầu.
Ví dụ: Quay đối tượng quanh trục song song với trục Ox, cách trục Oy, Oz một khoảng ty, tz
1 | 0 | 0 | 0 |
0 | 1 | 0 | 0 |
0 | −𝑡𝑦 | −𝑡𝑧 | 1 |
Có thể bạn quan tâm!
-
Xây Dựng Công Thức Biến Đổi Đối Tượng Khi Thực Hiện Các Phép Biến Đổi: -
Đồ họa máy tính - 16 -
Vật Thể Ba Chiều Được Biểu Diễn Bằng Mô Hình Khung Nối Kết -
Các Phép Chiếu Của Vật Thể Trong Không Gian Lên Mặt Phẳng -
Ảnh Của Phép Chiếu Trimetric Với Các Tham Số Góc Xoay Thay Đổi -
Phép Biến Đổi Mô Hình Và Phép Biến Đổi Hệ Trục Toạ Độ
Xem toàn bộ 240 trang tài liệu này.
Bước 1: Tịnh tiến sao cho trục quay trùng với trục Ox:
Ma trận biến đổi: T1= 0 0 1 0
1 | 0 | 0 | 0 |
0 cos 𝛼 sin 𝛼 0 | |||
0 | − sin 𝛼 | cos 𝛼 | 0 |
0 | 0 | 0 | 1 |
Bước 2: Quay quanh trục Ox: Ma trận biến đổi: T2=
1 | 0 | 0 | 0 |
0 | 1 | 0 | 0 |
0 | 𝑡𝑦 | 𝑡𝑧 | 1 |
Bước 3: Tịnh tiến ngược về vị trí ban đầu:
Ma trận biến đổi: T3= 0 0 1 0
Bước 4: Ma trận của phép quay quanh trục song song với trục Ox cách trục Oy, Oz 1 khoảng ty,tz là
1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 |
0 | 1 | 0 | 0 | 0 | cos 𝛼 | sin 𝛼 | 0 | 0 | 1 | 0 | 0 |
= 0 | 0 | 1 | 0 ∗ | 0 | − sin 𝛼 | cos 𝛼 | 0 | ||||
0 | −𝑡𝑦 | −𝑡𝑧 | 1 | 0 | 0 | 0 | 1 | 0 | 𝑡𝑦 | 𝑡𝑧 | 1 |
1 | 0 | 0 | 0 | ||||||||
0 | cos 𝛼 | sin 𝛼 | 0 | ||||||||
= 0 0 | − sin 𝛼 𝑡𝑦 ∗ 1 − cos 𝛼 + 𝑡𝑧 | ∗ sin 𝛼 | cos 𝛼 𝑡𝑧 ∗ (1 − cos 𝛼) − 𝑡𝑦 | ∗ sin 𝛼 | 0 1 | ||||||
T=T1*T2*T3
∗ 0 0 1 0
c. Phép quay quanh một trục bất kì
Giả sử trục quay đi qua hai điểm P0, P1 nào đó với phương được biểu diễn bởi vector đơn vị k. Quay điểm (x, y, z) quanh trục k theo một góc Ɵ sẽ biến thành điểm (x‘, y‘, z‘) (xem hình 5.13).
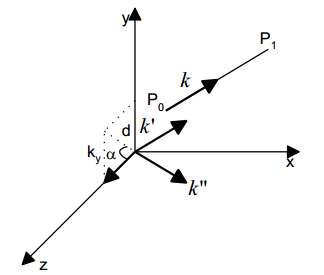
Hình 5.13 – Quay đối tượng quanh trục bất kỳ
Để thực hiện phép quay quanh k một góc Ɵ, ta có thể thực hiện một chuỗi các thao tác sau:
Tịnh tiến trục k về gốc tọa độ: tr(-P0) (thành trục k').
Quay quanh trục x một góc α để đặt trục k' nằm trên mặt phẳng Oxz: rot(x, α) (thành trục k‖).
Quay quanh trục y góc β để đưa trục k‖ về trục z: rot(y,- β). Thực hiện phép quay quanh trục z một góc Ɵ: rot(z, Ɵ).
Thực hiện chuỗi các phép biến đổi ngược lại quá trình trên.
Góc quay α được xác định dựa trên chiếu của k' lên mặt phẳng Oyz. Ta không cần tính α cụ thể. Thay vào đó ta tính sin(α) và cos(α) một cách trực tiếp.
Từ hình 5.13 ta có:
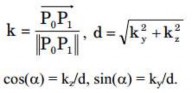
Tương tự, từ hình 5.14 ta có:
Như vậy, phép quay quanh một trục P0 P1 bất kì một góc , rot(P0P1, ), có thể được phân rã thành chuỗi các biến đổi cơ sở sau: tr(-P0) rot(x, α) rot(y, - β) rot(z, ) rot(y, β) rot(x, - α) tr(P0)
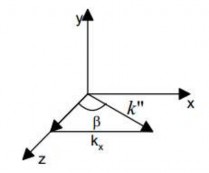
Hình 5.14 Tính góc β
5.3.5.Phép đối xứng.
a. Đối xứng qua mặt phẳng xOy.
Là phép biến đổi mà giá trị của x, y trong vector vị trí không thay đổi.
Giá trị của z = -z
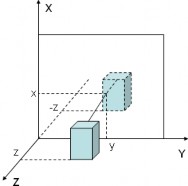
Hình 5.15 Đối xứng qua mặt phẳng xOy