Tổng Hợp Kỳ Vọng Chiều Hướng Tác Động Của Các Biến Trong Mô Hình Hồi Quy

PPEGt = (Rlt – Rht)

TSSL của danh mục các cổ phiếu có PEG nhỏ hơn hoặc bằng 1 tại thời điểm t (Rlt) là TSSL trung bình tính theo năm của các cổ phiếu niêm yết tại Sở giao dịch chứng khoán TPHCM có hệ số PEG nhỏ hơn hoặc bằng 1.

∑i Rilt nilt

Rlt

∑i n

1 ilt

Rilt là TSSL của cổ phiếu i tại thời điểm t trong danh mục cổ phiếu có hệ số PEG nhỏ hơn hoặc bằng 1.

nilt là số lượng đang lưu hành của cổ phiếu i tại thời điểm t trong danh mục cổ phiếu có hệ số PEG nhỏ hơn hoặc bằng 1.

TSSL của danh mục các cổ phiếu có PEG lớn hơn 1 tại thời điểm t (Rht) là TSSL trung bình tính theo năm của các cổ phiếu niêm yết tại Sở giao dịch chứng khoán TPHCM có hệ số PEG lớn hơn 1.

Rht

∑i Riht niht

∑i n

1 iht

Riht là TSSL của cổ phiếu i tại thời điểm t trong danh mục cổ phiếu có hệ số PEG lớn hơn 1.

niht là số lượng đang lưu hành của cổ phiếu i tại thời điểm t trong danh mục cổ phiếu có hệ số PEG lớn hơn 1.

PFSCORE: phần bù điểm số F_Score

Đây là phần chênh lệch TSSL của danh mục cổ phiếu có F_Score cao so với danh mục cổ phiếu có F_Score thấp4 (Piostroski, 2000), được tính theo công thức:

PFSCOREt = (Rhft – Rlft)

TSSL của danh mục cổ phiếu có điểm số F_ Score thấp tại thời điểm (t) (Rlft) là TSSL trung bình tính theo năm của các cổ phiếu niêm yết tại Sở giao dịch chứng khoán TPHCM có điểm số F_ Score thấp.

4 Điểm số F_Score cao là từ mức 6 trở lên, điểm số F_Score thấp là từ mức 4 trở xuống

Rlft

∑i Rilft nilft

∑i n

1 ilft

Rilft là TSSL của cổ phiếu i có điểm số F_ Score thấp tại thời điểm (t)

nilft là số lượng cổ phiếu i có điểm số F_ Score thấp tại thời điểm (t)

Tỷ sinh lời của danh mục cổ phiếu có điểm số F_ Score cao tại thời điểm t (Rhft) là TSSL trung bình tính theo năm của các cổ phiếu niêm yết tại Sở giao dịch chứng khoán TPHCM có điểm số F_ Score cao tại thời điểm (t).

∑i Rihft nihft

Rhft

∑i n

1 ihft

Rihft là TSSL của cổ phiếu i có điểm số F_ Score cao tại thời điểm (t)

nihft là số lượng cổ phiếu i có điểm số F_ Score cao tại thời điểm (t)

3.2.1.4. Kỳ vọng dấu của các biến trong mô hình

Giả thuyết 1: Hệ số PEG tác động tỷ lệ nghịch đến TSSL của cổ phiếu trong đầu tư giá trị trên TTCK Việt Nam.

Có nghĩa là những cổ phiếu có hệ số PEG càng thấp hơn 1 sẽ cho TSSL cao hơn. Giả thuyết này được chứng minh trong nghiên cứu của Schatzberg và Vora (2009) và. Lynch (1989). Theo Lynch (1989), khi cổ phiếu có PEG thấp hơn 1, có nghĩa là cổ phiếu này đang bị định giá thấp hơn tốc độ tăng trưởng của nó, vì vậy, trong tương lai giá cổ phiếu sẽ tăng trở lại, điều này sẽ làm tăng TSSL của cổ phiếu. Vì vậy, NCS kỳ vọng biến PPEG sẽ tỷ lệ thuận với biến RIRF trong mô hình kinh tế.

Giả thuyết 2: Điểm số F_Score tác động tỷ lệ thuận đến TSSL của cổ phiếu trong đầu tư giá trị trên TTCK Việt Nam.

Có nghĩa là những cổ phiếu có điểm số F_Score cao sẽ cho TSSL cao hơn những cổ phiếu có điểm số F_Score thấp. Giả thuyết này được chứng minh trong nghiên cứu của Piotroski (2000), Mohr (2012), Galdi và cộng sự (2013), Hyde (2014) và Võ Thị Quý & Bùi Thanh Trúc (2015). Theo Piotroski (2000), khi cổ phiếu có điểm số F_Score cao, điều đó chứng tỏ công ty có sức khỏe tài chính tốt, vì vậy, nhà đầu tư sẽ sẵn sàng trả

giá cao hơn trong tương lại. Vì vậy, NCS kỳ vọng biến PFSCORE sẽ tỷ lệ thuận với biến RIRF trong mô hình kinh tế.

 Theo nghiên cứu mô hình 3 nhân tố của Fama & French (1992) và Athanassakos (2013), thì TSSL của thị trường sẽ tỷ lệ thuận và quy mô của công ty sẽ tỷ lệ nghịch với TSSL của cổ phiếu. Vì vậy, NCS kỳ vọng biến RMRF và PMARKETCAP tỷ lệ thuận với biến RIRF trong mô hình kinh tế.

Bảng 3.1: Tổng hợp kỳ vọng chiều hướng tác động của các biến trong mô hình hồi quy

Mã

Tên	Loại biến	Chiều hướng tác động	Căn cứ
RIRF	Chênh lệch TSSL của cổ phiếu so với lãi suất phi rủi ro	Phụ thuộc
RMRF	Phần bù thị trường	Độc lập	Tỷ lệ thuận với RIRF	Theo Fama & French (1992), Athanassakos (2013)
PMARKETCAP	Phần bù quy mô	Độc lập	Tỷ lệ thuận với RIRF	Theo Fama & French (1992), Athanassakos (2013)
PPEG	Phần bù định giá	Độc lập	Tỷ lệ thuận với RIRF	Theo Schatzberg và Vora (2009) và Lynch (1989)
PFSCORE	Phần bù điểm số F_Score	Độc lập	Tỷ lệ thuận với RIRF	Theo Piotroski (2000), Mohr (2012), Galdi và cộng sự (2013), Hyde (2014) và Võ Thị Quý & Bùi Thanh Trúc (2015)

Có thể bạn quan tâm!

Xem toàn bộ 211 trang tài liệu này.

Nguồn: NCS tổng hợp

3.2.1.5. Quy trình nghiên cứu

Luận án thực hiện mô hình hồi quy theo quy trình nghiên cứu như sau:

Hinh 3.1: Quy trình nghiên cứu

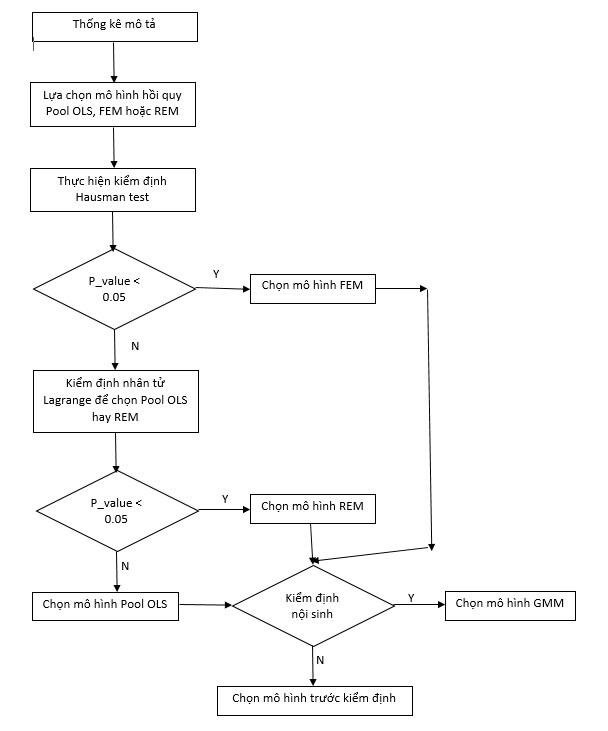
Nguồn: theo tác giả

Bước 1: Thống kê mô tả dữ liệu

Thống kê mô tả được được sử dụng để mô tả các đặc điểm của dữ liệu thông qua các tiêu chí cơ bản như giá trị trung bình, giá trị nhỏ nhất, giá trị lớn nhất, giá trị trung vị, phương sai và độ lệch chuẩn. Từ đó, xem xét dữ liệu bình thường hay có bị khuyết tật gì hay không, qua đó, tăng độ tin cậy của dữ liệu.

Bước 2: Lựa chọn các mô hình hồi quy để ước lượng tham số của mô hình

Luận án sử dụng dữ liệu bảng không cân bằng để tiến hành ước lượng hồi quy với các phương pháp ước lượng Pooled OLS, mô hình tác động ngẫu nhiên (Random Effect Model), mô hình tác động cố định (Fixed Effect Model) và kiểm định các giả thuyết vững của mô hình. Nếu như mô hình có khuyết tật thì sẽ sử dụng các phương pháp hồi quy GMM để khắc phục.

Đầu tiên, NCS sử dụng kiểm định Hausman test để lựa chọn giữa mô hình FEM và REM. Bản chất của mô hình này là bản chất của kiểm định này là kiểm tra sự tự tương quan của sai số với biến độc lập. Nếu P_value nhỏ hơn 0.05, chứng tỏ sai số và biến độc lập có tương quan không có sự ngẫu nhiên, vì vậy, sẽ lựa chọn mô hình FEM.

Ngược lại, nếu P_value lớn hơn 0.05, chứng tỏ sai số và biến độc lập là ngẫu nhiên, không tương quan. Trong trường hợp này, phải sử dụng kiểm định nhân tử Lagrange để lựa chọn mô hình REM hoặc Pool OLS. Bản chất của kiểm định nhân tử là xem xét mô hình REM có bị phương sai sai số thay đổi không. Nếu P_value nhỏ hơn 0.05, chứng tỏ có hiện tượng phương sai sai số thay đổi, vì vậy, chọn mô hình REM để ước lượng. Ngược lại, nếu P_value lớn hơn 0.05, chứng tỏ không có hiện tượng phương sai sai số thay đổi, do đó, lựa chọn mô hình Pooled OLS để ước lượng.

Bước 3: Kiểm định khuyết tật của mô hình hồi quy được lựa chọn

Sau khi đã lựa chọn được một trong ba mô hình Pooled OLS, FEM hoăc REM, để đảm bảo kết quả ước lượng của các mô hình này đáng tin cậy, cần phải thực hiện kiểm định các khuyết tật của mô hình. Nếu xảy ra một hoặc các khuyết tật sau: phương sai sai số thay đổi, tự tương quan hoặc nội sinh, thì NCS sẽ sử dụng mô hình GMM thay thế các mô hình trên để ước lượng tham số.

3.2.1.6. Các mô hình hồi quy ước lượng tham số

Phương pháp ước lượng hồi quy Pooled OLS có một giả định quan trọng là hệ số hồi quy không thay đổi theo thời gian. Về bản chất cơ bản thì đây chính là ước lượng bình phương nhỏ nhất như thông thường khi bỏ qua yếu tố chuỗi thời gian (kí hiệu chiều t) và dữ liệu bảng cũng xem như dữ liệu chéo. Tất nhiên, khi sử dụng phương pháp hồi quy này thì năm giả định nghiêm ngặt của OLS bắt buộc phải đảm bảo và rất dễ có khả năng xảy ra sai số chuẩn lớn, làm cho kết quả chệch và không vững, các giả thuyết này bao gồm:

- Mô hình là tuyến tính và các biến độc lập trong ma trận X không ngẫu nhiên.

- Các sai số có phân phối chuẩn với giá trị trung bình bằng 0: E(εi|X1i, X2i, … , Xki) = 0.

- Phương sai sai số không đổi, nghĩa là var(εi|X1i, X2i, … , Xki)= σ2 = const.

- Các sai số không có tương quan với nhau Cov(εi, εj ) = 0 ∀ i ≠j

- Các biến độc lập trong mô hình không cộng tuyến (hay tương quan) với nhau (hiện tượng đa công tuyến) và không cộng tuyến với sai số của mô hình (hiện tượng nội sinh, hiện tượng này xảy ra sẽ dẫn đến trung bình của các sai số khác 0).

Mô hình hiệu ứng tác động cố định (FEM) xem xét đến ảnh hưởng của cả hiệu ứng thời gian và hiệu ứng không gian lên đối tượng quan sát. Khi xem xét ảnh hưởng của hiệu ứng thời gian, hệ số chặn (α) có thể thay đổi giữa các năm (thay đổi theo t), tuy nhiên, trong 1 năm thì không thay đổi đối với những doanh nghiệp khác nhau (không thay đổi theo i). Khi xem xét ảnh hưởng của hiệu ứng không gian, hệ số chặn có thể thay đổi giữa các doanh nghiệp khác nhau tuy nhiên không thay đổi qua các năm. Cuối cùng khi kết hợp hiệu ứng không gian và hiệu ứng thời gian ta được mô hình hoàn chỉnh. Tùy bản chất của sự kiện nghiên cứu và tùy kết quả kiểm định mà sẽ chọn mô hình FEM theo không gian, thời gian hay cả hai. Mô hình hiệu ứng tác động cố định rõ ràng ưu điểm hơn so với mô hình kết hợp tất cả các quan sát, tuy nhiên, hạn chế lớn nhất của mô hình là tạo ra nhiều biến giả nên dẫn đến trường hợp đa cộng tuyến giữa các biến giả.

Mô hình hiệu ứng tác động ngẫu nhiên (REM) tương đối giống với FEM, tuy nhiên đối với FEM, hệ số chặn thay đổi qua thời gian và thay đổi đối với mỗi doanh nghiệp thì

với REM hệ số chặn được cố định, giá trị của nó bằng giá trị trung bình của các hệ số chặn trong FEM. Sự khác nhau giữa hệ số này được đưa vào sai số ngẫu nhiên (εi). Như vậy, trong REM sai số ngẫu nhiên tách làm hai thành phần: một là sai số ngẫu nhiên theo mỗi doanh nghiệp, hai là sai số ngẫu nhiên của mô hình. Mặc dù, REM giảm thiểu được bất lợi của FEM khi không sử dụng biến giả, tuy nhiên, một trong những giả định đặc biệt quan trọng của REM là không tồn tại tương quan nào giữa thành phần sai số ngẫu nhiên của mỗi quan sát và các biến độc lập (có hiện tượng nội sinh), đồng thời, mỗi quan sát được chọn ngẫu nhiên từ tổng thể. Tuy nhiên, các doanh nghiệp lựa chọn đưa vào mô hình không ngẫu nhiên, từ đó làm hạn chế kết quả của mô hình.

Mô hình System GMM: Lars Peter Hansen (1982) giới thiệu về phương pháp ước lượng GMM (Generalized Methods of Moments) khi đề cập đến hai loại Difference GMM (DGMM) được phát triển bởi Arellano và Bond (1991) và System GMM (SGMM) được phát triển bởi Arellano và Bover (1995); Blundell và Bond (1998). Sự khác biệt rõ rệt của hai phương pháp ước lượng này là dùng sai phân (difference) để loại bỏ đi khuyết tật nội sinh trong mô hình, sử dụng chính biến trễ của biến phụ thuộc làm công cụ để khắc phục. Trong khi, đó system GMM lại sử dụng hệ thống biến công cụ và biến ngoại sinh để nhằm giải quyết hiện tượng ước lượng thiếu bền vững trong mô hình. Do đó, ước lượng hồi quy system-GMM có nhiều giả định và kết quả nếu thỏa mãn sẽ cho ra ước lượng vững, không chệch hơn so với difference-GMM. Bên cạnh đó, các tác giả Bond (2002), Baum (2006) cũng ủng hộ quan điểm rằng system GMM sẽ cho ra kết quả tin cậy hơn rất nhiều.

Bất kì phương pháp hồi quy nào cũng đảm bảo những giả định quan trọng của tính vững và ước lượng không chệch (trung bình của các sai số bằng 0). Tuy nhiên, đối với dữ liệu bảng hồi quy thì cần kiểm định chặt chẽ phần dư của mô hình với sự tác động đến biến phụ thuộc và các biến độc lập trong mô hình để đảm bảo khuyết điểm mô hình không có và kết quả đáng tin cậy. GMM cần kiểm định chặt chẽ phần dư và sự tương quan của các chuỗi AR(1) cũng như AR(2). Kiểm định tự tương quan phần dư của phương pháp hồi quy GMM được hiểu như sau:

Giả thuyết H0: không có sự tự tương quan bậc một (kiểm định AR(1)) hoặc bậc hai (kiểm định AR(2)) của phần dư. Hoặc trong một vài nội dung kinh tế lượng gần đây thì

không cần quan tâm tương quan bậc 1 mà cần đảm bảo rằng tương quan bậc 2 không tồn tại.

Điều đó có nghĩa rằng p-value của AR(1) nhỏ hơn 0.05 hoặc không quan tâm nhưng p- value của AR(2) chắc chắn phải lớn 0.05 tại mức ý nghĩa 5% để đảm bảo không có tương quan của phần dư bậc 2.

3.2.1.7. Kiểm định các khuyết tật của mô hình hồi quy

Kiểm định hiện tượng đa cộng tuyến: Đa cộng tuyến là hiện tượng các biến độc lập trong mô hình có mối quan hệ với nhau (Nguyễn Quang Dong & Nguyễn Thị Minh, 2013). Đa cộng tuyến hoàn hảo làm cho mô hình không ước lượng được. Đa cộng tuyến không hoàn hảo có thể làm cho các biến độc lập cộng tuyến mất đi ý nghĩa trong mô hình hoặc có thể bị sai dấu của hệ số hồi quy. Luận án sẽ sử dụng nhân tử phóng đại phương sai VIF để kiểm định hiện tượng đa công tuyến, nếu VIF của các biến độc lập nhỏ hơn 10 chứng tỏ không có hiện tượng đa cộng tuyến; ngược lại nếu VIF lớn hơn 10, chứng tỏ có hiện tượng đa cộng tuyến. Trong trường hợp xảy ra hiện tượng đa cộng tuyến, sẽ xử lý bằng cách loại bổ biến độc lập có hệ số VIF lớn hơn 10, sau đó, chạy lại kết quả hồi quy.

Kiểm định hiện tượng phương sai sai số thay đổi: hiện tượng phương sai thay đổi xảy ra khi phương sai của sai số không phải là hằng số (Nguyễn Quang Dong & Nguyễn Thị Minh, 2013). Nếu hệ số quy hồi ước lượng được cho là vững và không chệch, thì các giá trị của phần dư phải tuân theo phân phối ngẫu nhiên và có phương sai không đổi. Nếu chúng thay đổi, phương trình ước lượng được sẽ không chính xác hoặc đã bỏ qua những biến độc lập quan trọng tác động tới biến phụ thuộc. Để phát hiện hiện tượng phương sai sai số không đổi, luận án sử dụng kiểm định Breusch – Pagan (hettest); nếu p-value < 0.05, có nghĩa là có hiện tượng phương sai sai số thay đổi; ngược lại nếu p- value > 0.05, có nghĩa là không có hiện tượng phương sai sai số thay đổi. Trong trường hợp có hiện tượng phương sai sai số thay đổi, luận án sẽ khắc phục bằng cách sử dụng mô hình hồi quy GMM để ước lượng tham số.

Kiểm định hiện tượng tự tương quan: hiện tượng tự tương quan xảy ra khi các sai số không ngẫu nhiên mà có sự tương quan với nhau (Gujarati, 2009). Hiện tượng tự tương quan cũng làm cho ước lượng OLS không còn là ước lượng hiệu quả nhất và các kiểm