học là một hoạt động phức tạp, bao gồm sự chuyển đổi giữa toán học và thực tế theo cả hai chiều, vì vậy đòi hỏi phải có nhiều năng lực khác nhau trong các lĩnh vực toán học cũng như có kiến thức liên quan đến các tình huống thực tế được xem xét.
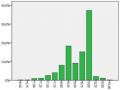
Qui trình mô hình hóa toán học được đề xuất bởi OECD/PISA (2009) mô tả trong Hình 4.1, thường được gọi là quá trình toán học hóa, đó là một quá trình cơ bản mà HS dùng để giải quyết các vấn đề thực tế được đề cập.
Lời giải thực tế
5
Thế giới thực tế
Lời giải toán học
4
Thế giới toán học
5
Vấn đề thực tế
Vấn đề toán học
1, 2, 3
Hình 4.1. Quy trình toán học hóa của OECD/PISA (2009) Trong đó:
(1) Bắt đầu từ một vấn đề được đặt ra trong thực tế.
(2) Tổ chức nó theo các khái niệm toán học.
(3) Không ngừng cắt tỉa thực tế.
(4) Giải quyết bài toán.
(5) Làm cho lời giải có ý nghĩa theo bối cảnh thực tế.
Như vậy, để giải quyết một vấn đề thực tế, HS cần chuyển vấn đề thực tế thành một dạng toán, toàn bộ quá trình được tiếp tục trong toán học. Các em sẽ nỗ lực làm việc trên mô hình của mình về bối cảnh vấn đề, để điều chỉnh nó, để thiết lập các quy tắc, để xác định các nối kết và để sáng tạo nên một lập luận toán học đúng đắn. Chúng tôi sẽ vận dụng lý thuyết GQVĐ trong dạy học toán và mô hình hóa toán học của OECD/PISA (2009) trong xây dựng các câu hỏi đánh giá năng lực SLTKYH của SV y khoa khi GQVĐ thực tế.
4.2. Mô hình đánh giá năng lực Suy luận thống kê y học của sinh viên khi giải quyết vấn đề thực tế
Theo OECD (2003) “PISA không phải là một cuộc sát hạch khả năng học thuộc lòng lượng kiến thức trong sách vở hay nặng về việc thành thạo chương trình ở trường, mà PISA chú trọng đến các kiến thức quan trọng và những kỹ năng cần thiết cho cuộc sống trưởng thành”. Mục tiêu đánh giá của PISA là xem xét khả năng vận dụng một cách linh hoạt các kiến thức và kỹ năng trong các lĩnh vực chuyên môn cơ bản vào các bối cảnh và vấn đề mới mà HS bắt gặp trong cuộc sống thực tế. PISA chú trọng vào việc thành thạo các quá trình, việc hiểu các khái niệm và khả năng xử lý các tình huống khác nhau trong mỗi lĩnh vực. Chúng tôi nhận thấy quan điểm này của PISA là phù hợp với mục tiêu đánh giá năng lực SLTKYH của SV y khoa khi GQVĐ thực tế. Học toán vì cuộc sống là một quan điểm của PISA. Đánh giá lĩnh vực Hiểu biết toán bao gồm các năng lực của HS để phân tích, suy luận, giao tiếp các ý tưởng toán học một cách hiệu quả khi các em đặt, thiết lập, giải và giải thích các lời giải cho các vấn đề toán trong nhiều bối cảnh khác nhau. Đánh giá liên quan đến Nội dung toán học (các ý tưởng bao quát), Quá trình toán học (xác định bởi các năng lực toán học) và Bối cảnh trong đó toán học được sử dụng. Vận dụng quan điểm đánh giá Hiểu biết toán của PISA, chúng tôi đề xuất một mô hình đánh giá năng lực SLTKYH của SV y khoa khi GQVĐ thực tế thể hiện như trong Hình 4.2 dưới đây.
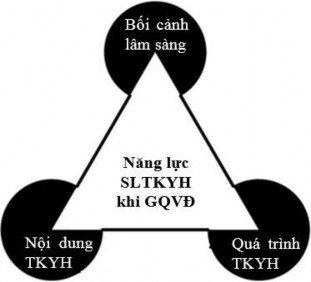
Hình 4.2. Mô hình đánh giá năng lực SLTKYH của SV khi GQVĐ thực tế
Trong mô hình này, đánh giá liên quan đến ba khía cạnh là Nội dung TKYH (bao gồm các ý tưởng cơ bản sử dụng để GQVĐ), Quá trình TKYH thể hiện năng lực SLTKYH (xác định bởi ba năng lực SLTKYH là năng lực Mô tả, Giải thích, Dự đoán) và Bối cảnh lâm sàng trong đó sử dụng SLTKYH. Trong Bối cảnh thực tế liên quan đến lâm sàng y học gắn liền với cuộc sống nghề nghiệp, đòi hỏi khả năng áp dụng các kiến thức, kỹ năng TKYH và SLTKYH đã học liên quan trong bối cảnh ít có cấu trúc hơn, SV phải đưa ra quyết định về kiến thức nào có thể liên quan, quy trình hay thủ tục nào sẽ dẫn đến giải pháp khả thi và sử dụng SLTKYH ở các mức độ khác nhau. Nội dung TKYH nên tập trung vào các ý tưởng lớn của TKYH, bao gồm Dữ liệu; Phân phối; Xu hướng; Biến thiên; Mô hình; Mối liên quan; Mẫu và lấy mẫu; và Suy diễn thống kê.
4.3. Thang đánh giá năng lực Suy luận thống kê y học của SV khi giải quyết vấn đề thực tế
Các năng lực SLTKYH được mô tả theo ba cụm năng lực nhận thức như trong Bảng 4.1. Trong thang đánh giá tổng quát năng lực SLTKYH chúng tôi đã đề xuất gồm sáu mức độ từ thấp đến cao tương ứng với ba cụm năng lực tái tạo, liên kết và phản ánh (xem Bảng 2.8). Trong đó mức 1, 2 tương ứng với cụm tái tạo, mức 3, 4 tương ứng với cụm liên kết và mức 5, 6 tương ứng với cụm phản ánh.
Bảng 4.1. Ma trận hai chiều của ba năng lực SLTKYH và ba cụm năng lực
Tái tạo | Liên kết | Phản ánh | ||||
Mức 1 | Mức 2 | Mức 3 | Mức 4 | Mức 5 | Mức 6 | |
Mô tả | – | – | – | – | – | – |
Giải thích | – | – | – | – | – | – |
Dự đoán | – | – | – | – | – | – |
Có thể bạn quan tâm!
-
Hình Thức Kiểm Tra, Đánh Giá Đã Và Đang Áp Dụng Trong Dạy Học Thống Kê Y Học -
Giải Pháp 2: Cập Nhật Nội Dung Kiến Thức Trong Giáo Trình Gt V -
Giải Pháp 3: Khai Thác Ứng Dụng Của Công Cụ Công Nghệ Thúc Đẩy Khả Năng Tự Học Của Sinh Viên -
Thiết Kế Bộ Công Cụ Đánh Giá Năng Lực Suy Luận Thống Kê Y Học Của Sv Khi Giải Quyết Vấn Đề Thực Tế -
Liệt Kê 14 Vấn Đề Có Bối Cảnh Lâm Sàng Y Học -
Ma Trận Đề Kiểm Tra Đánh Giá Năng Lực Sltkyh (Ma Trận 2)
Xem toàn bộ 200 trang tài liệu này.
Các mức năng lực nhận thức của mỗi năng lực SLTKYH Mô tả, Giải thích, Dự đoán được mô tả cụ thể. Chúng tôi xác định mức 1, 2, 3 được xem là các mức độ tư duy bậc thấp và mức 4, 5, 6 là các mức độ tư duy bậc cao.
4.3.1. Thang đánh giá năng lực SLTKYH Mô tả
Chúng tôi đã trình bày trong mục 2.2.2, năng lực SLTKYH Mô tả có thể xem là khả năng thực hiện một cách hiệu quả và khoa học các nhiệm vụ trong quá trình TKYH Mô tả. Theo đó, năng lực SLTKYH Mô tả có thể được tóm tắt bởi ba thành tố then chốt là:
- Mô tả dữ liệu, tổ chức và biểu diễn dữ liệu.
- Mô tả quá trình tạo ra dữ liệu: mô tả quá trình lấy mẫu, các phân phối lấy mẫu.
- Tạo ra những giả thuyết khoa học cần được kiểm tra: hình thành những dự đoán ban đầu liên quan đến tổng thể.
Như vậy, năng lực SLTKYH Mô tả có liên quan đến các loại SLTKYH bao gồm suy luận về dữ liệu, suy luận về các biểu diễn dữ liệu, suy luận về các đại lượng thống kê. Thang đánh giá năng lực này được chúng tôi mô tả cụ thể trong Bảng 4.2 dưới đây.
Bảng 4.2. Thang đánh giá năng lực SLTKYH Mô tả
Mức độ | Mô tả về nhiệm vụ | |
Phản ánh | 6 | - Sử dụng các mức suy luận bậc cao trong bối cảnh thống kê để tạo nên các biểu diễn toán học cho các tình huống thực tế y học. - Sử dụng sự hiểu biết sâu sắc, sự phản ánh và lập luận để giao tiếp chính xác các kết quả. |
5 | - Áp dụng việc hiểu sâu sắc các kiến thức thống kê liên quan thống kê mô tả, quá trình lấy mẫu và các phân phối lấy mẫu trong các tình huống nghiên cứu y học phức tạp theo nghĩa nào đó là có cấu trúc và biểu diễn toán học phần nào thể hiện rò. - Sử dụng sự thấu hiểu suy luận để lý giải thông tin hay một kết quả đã cho và hình thành dự đoán ban đầu liên quan đến tổng thể trong một bối cảnh thực tế y học. - Phản ánh các hoạt động của mình, thành lập và giao tiếp các lý giải, suy luận. | |
4 | - Chọn lựa phương pháp thống kê để tóm tắt, mô tả dữ liệu phù hợp trong một tình huống mới với một bối cảnh lâm sàng cụ thể. - Sử dụng lập luận dựa trên việc lý giải các dữ liệu và các tóm tắt thống kê (tóm tắt kiểu số và hình ảnh): mô tả toàn thể qui luật |
của sự biến thiên bao gồm mô tả các phân phối của dữ liệu, các đặc trưng về hình dáng, tâm, độ phân tán, so sánh các phân phối khác nhau dựa trên các đặc trưng này. - Áp dụng việc hiểu các khái niệm then chốt như biến thiên, trung bình, hình dáng và kết hợp các quy tắc (định lý giới hạn trung tâm) với yếu tố ngẫu nhiên để mô tả các đặc trưng của quá trình lấy mẫu, các phân phối lấy mẫu. - Kiến tạo và giao tiếp các giải thích, lập luận: Lý giải lời văn, chuyển mô tả bằng lời văn thành các bài toán thống kê. | ||
3 | - Giải thích tại sao kiểu dữ liệu sẽ dẫn đến một loại bảng, đồ thị cụ thể. Giải thích ý nghĩa các thuật ngữ, kí hiệu thống kê như các đo lường thống kê về tâm, độ phân tán. - Giải thích thông tin và dữ liệu. Giải thích thông tin từ các biểu diễn dữ liệu. Liên kết các nguồn thông tin khác nhau: Lý giải thông tin được đưa vào bảng, các khía cạnh của biểu diễn dữ liệu, liên kết dữ liệu với dạng đồ thị phù hợp. - Giải thích các biểu diễn dữ liệu bằng đồ thị và mô tả các phân phối của dữ liệu, các đặc trưng về hình dáng, tâm, độ phân tán. Mô tả hình dáng toàn thể của một phân phối, quen thuộc với các hình dáng phổ biến của các phân phối như chuẩn, lệch trái, lệch phải. - Giải thích khái niệm mẫu ngẫu nhiên, phân biệt một thống kê mẫu và một tham số tổng thể. Giải thích quá trình lấy mẫu và một vài ý nghĩa của định lý giới hạn trung tâm trong việc mô tả đặc điểm của phân phối lấy mẫu. | |
Tái tạo | 2 | - Đọc các dữ liệu thô hay dữ liệu biểu diễn trong các bảng, biểu đồ hay đồ thị bao gồm chỉ ra được các tính năng hiển thị và xác định đơn vị của các giá trị dữ liệu. - Sắp xếp, phân loại hay củng cố dữ liệu thành một dạng tóm tắt bao gồm nhóm dữ liệu, tóm tắt dữ liệu bởi các đo lường thống kê. - Thực hiện một số kĩ năng cơ bản của thống kê như xây dựng và biểu diễn bởi các bảng biểu, đồ thị cho một tập dữ liệu đã cho và làm việc với các biểu diễn khác nhau của dữ liệu. |
1 | - Nhận ra và phân loại dữ liệu định tính hay định lượng, rời rạc hay liên tục. Nhận ra được thuật ngữ và kí hiệu thống kê quen thuộc. - Xác định các thông tin thống kê được trình bày theo các dạng bảng biểu và đồ thị quen thuộc. - Áp dụng trực tiếp các công thức, thủ tục đã cho để xác định các đo lường thống kê. |
4.3.2. Thang đánh giá năng lực SLTKYH Giải thích
Năng lực SLTKYH Giải thích có thể xem là khả năng thực hiện một cách hiệu quả và khoa học các nhiệm vụ trong quá trình TKYH Giải thích. Theo đó, năng lực SLTKYH Giải thích có thể được tóm tắt bởi bốn thành tố then chốt là:
- Nhận ra các xu hướng trong các dữ liệu, sử dụng các đại lượng thống kê mô tả từ mẫu để suy luận và dự đoán về đặc trưng của tổng thể.
- Kiểm định các giả thuyết khoa học: tổng quát hóa các kết luận về tổng thể trên cơ sở của mẫu. Thông thường, đầu tiên là hình thành các giả thuyết thống kê, thường ở dạng khác với giả thuyết lâm sàng. Sử dụng dữ liệu mẫu để kiểm tra các giả thuyết này. Thủ tục kiểm định là một trường hợp đặc biệt của lý thuyết quyết định hai lựa chọn, trong đó chiến lược quyết định chỉ sử dụng một tổn thất, đó là rủi ro (xác suất) khi đưa ra quyết định sai lầm. Cụ thể hơn, tổn thất là đo lường được, kiểm soát xác suất của mỗi một trong hai loại sai lầm có thể xảy ra: chọn giả thuyết H0 khi giả thuyết H1 đúng và chọn giả thuyết H1 khi giả thuyết H0 đúng.
- Lý giải tính hợp lý của các kết quả dựa trên các ý tưởng về mối quan hệ giữa mẫu và tổng thể, tính đại diện của mẫu đối với tổng thể của nó.
- Lý giải về khả năng xảy ra của các kết quả bằng cách sử dụng việc hiểu các ý tưởng về ngẫu nhiên, cơ hội và tính không chắc chắn.
Như vậy, năng lực SLTKYH Giải thích có liên quan đến các loại SLTKYH bao gồm suy luận về các đại lượng thống kê, suy luận về các mẫu, suy luận về tính không chắc chắn và suy luận về mối liên hệ. Thang đánh giá năng lực này được chúng tôi mô tả cụ thể trong Bảng 4.3.
Bảng 4.3. Thang đánh giá năng lực SLTKYH Giải thích
Mức độ | Mô tả về nhiệm vụ | |
Phản ánh | 6 | - Giải thích các quá trình thống kê và có thể giải thích một cách đầy đủ các kết quả thống kê. - Sử dụng mức tư duy bậc cao và các kĩ năng suy luận trong bối cảnh thống kê để tạo nên các biểu diễn toán học cho các tình huống thực tế y học. - Sử dụng sự hiểu biết sâu sắc, sự phản ánh và lập luận để giao tiếp chính xác các kết quả. |
5 | - Áp dụng việc hiểu sâu sắc các kiến thức thống kê liên quan thống kê mô tả, quá trình lấy mẫu, các phân phối lấy mẫu, phương pháp ước lượng tham số, kiểm định giả thuyết thống kê trong các tình huống nghiên cứu y học phức tạp theo nghĩa nào đó là có cấu trúc và biểu diễn toán học phần nào thể hiện rò. - Sử dụng sự thấu hiểu suy luận để lý giải thông tin đã cho, kiểm chứng và lý giải một kết quả đã cho trong một bối cảnh thực tế y học. - Lập hay làm việc hiệu quả với các giả thuyết cho một tình huống thực tế y học,với những mô hình phức tạp. - Phản ánh các hoạt động của mình, thành lập và giao tiếp các lý giải, suy luận. | |
4 | - Áp dụng các khái niệm xác suất, thống kê cơ bản kết hợp với suy luận logic trong các tình huống ít quen thuộc. - Chọn lựa và tích hợp các phương pháp thống kê suy luận ước lượng tham số hay kiểm định giả thuyết để suy ra các đặc trưng hay các kết luận liên quan đến tổng thể phù hợp trong một tình huống mới với một bối cảnh lâm sàng cụ thể. - Áp dụng việc hiểu các khái niệm then chốt như mẫu ngẫu nhiên, các phân phối lấy mẫu và kết hợp các quy tắc với yếu tố ngẫu nhiên để mô tả, lý giải phân phối của các hàm ước lượng, hàm kiểm định. |
- Sử dụng lập luận để giải thích các quá trình thống kê và giải thích đầy đủ các kết quả thống kê: lý giải việc chọn phương pháp ước lượng, test thống kê là phù hợp; lý giải tính hợp lý của các kết quả mối quan hệ giữa mẫu và tổng thể, tính đại diện của mẫu đối với tổng thể của nó. - Kiến tạo và giao tiếp các giải thích, lập luận: Lý giải lời văn bao gồm trong một tình huống khoa học không quen thuộc; chuyển mô tả bằng lời văn thành các bài toán thống kê. | ||
3 | - Giải thích thông tin và dữ liệu. Liên kết các nguồn thông tin khác nhau. Chuyển đổi thông tin từ dạng này sang dạng khác, từ một khái niệm này sang khái niệm khác. - Giải thích các khái niệm, công thức về hàm ước lượng, ước lượng điểm cho tham số tổng thể, khoảng tin cậy, độ tin cậy, thống kê ước lượng, giả thuyết thống kê, hàm kiểm định, miền bác bỏ giả thuyết theo nghĩa quá trình. - Giải thích các quy trình, thuật toán từng bước ước lượng tham số, kiểm định giả thuyết thống kê trong bối cảnh y học. - Từ một vấn đề thực tế trong nghiên cứu y học, xây dựng và giải thích các giả thuyết thống kê liên quan đến tham số của tổng thể, đến sự phù hợp, đến mối liên hệ giữa hai biến định tính, phân biệt với các giả thuyết lâm sàng y học. - Chọn và áp dụng các phương án để giải quyết vấn đề đơn giản theo phương pháp ước lượng tham số, kiểm định giả thuyết thống kê. | |
Tái tạo | 2 | - Truy hồi lại được các công thức, thuật toán, quy tắc, quy ước và các quy trình từng bước trong bài toán ước lượng tham số của tổng thể và kiểm định giả thuyết thống kê. - Giải thích hay đọc các kết quả của thủ tục thống kê đơn giản áp dụng trong tình huống không đòi hỏi nhiều hơn sự kết luận trực tiếp. - Thực hiện quy trình, thuật toán ước lượng tham số, kiểm định giả thuyết thống kê trong bối cảnh y học tương tự, quen thuộc. |