Mô Hình Nghiên Cứu Mối Quan Hệ Giữa Lợi Nhuận Cổ Phiếu Ngân Hàng Và Các

Dựa vào các chỉ tiêu AIC, SIC cùng kiểm định Lagrange Multiplier test (ARCH LM test) để lựa chọn p, q phù hợp nhất cho phương trình hồi quy ARCH hoặc GARCH.

Biến động lãi suất qua đêm liên ngân

hàng

Biến động tỷ giá

USD/VND

Biến động lãi suất TPCP 5

năm

Chính sách ổn định tỷ giá

1/12/2011

Thay đổi lãi suất

qua đêm liên

ngân hàng

Biến động lợi nhuận cổ phiếu

ngân hàng

Thay đổi tỷ giá bình quân liên ngân hàng

USD/VND

Thay đổi lãi suất TPCP 5

năm

LỢI NHUẬN CỔ

PHIẾU NGÂN HÀNG

THAY ĐỔI LÃI SUẤT

TIỀN GỬI

THAY ĐỔI LÃI SUẤT

CHO VAY

THAY ĐỔI LÃI SUẤT

CHIẾT KHẤU

MÔ HÌNH NGHIÊN CỨU

Ghi ghú: Mũi tên chỉ hướng tác động

Hình 1.1: Mô hình nghiên cứu mối quan hệ giữa lợi nhuận cổ phiếu ngân hàng và các biến

CHƯƠNG 2: NGUỒN DỮ LIỆU VÀ PHƯƠNG PHÁP

NGHIÊN CỨU

2.1. Dữ liệu nghiên cứu:

Dữ liệu nghiên cứu bao gồm chỉ số VN-index đại diện cho toàn thị trường và chỉ số ngành ngân hàng VNBank-index (bao gồm: ACB, CTG, VCB, CTS, EIB, NVB, SHB, STB)9 được thu thập từ trang web cophieu68.com đại diện cho nhóm cổ phiếu ngân hàng. Dữ liệu lãi suất qua đêm liên ngân hàng, tỷ giá bình quân liên ngân hàng

USD/VND được thu thập từ trang web NHNN (sbv.com.vn). Lãi suất TPCP 5 năm được thu thập từ nguồn dữ liệu Bloomberg. Rm, Rb lần lượt là lợi nhuận tính theo ngày của thị trường và nhóm cổ phiếu ngành ngân hàng trong giai đoạn từ 2/1/2009 đến 12/3/2013 (gồm 626 quan sát) thu thập từ trang web cophieu68.com. Dữ liệu lãi suất cho vay, lãi suất tiền gửi và lãi suất chiết khấu theo tháng được thu thập từ nguồn dữ liệu IMF từ tháng 1/2009 đến 7/2012.

Bảng 2.1: Các biến sử dụng trong mô hình (đơn vị: %)

STT

Tên biến	Nội dung	Công thức tính
1	Rb,t	Lợi nhuận cổ phiếu ngân hàng	Rb,t =
2	Rm,t	Lợi nhuận thị trường	Rm,t =
3	EXC	Thay đổi tỷ giá USD/VND	EXCt =
4	OIRC	Thay đổi lãi suất qua đêm liên ngân hàng	OIRCt =
5	GR5C	Thay đổi lãi suất TPCP 5 năm	GR5Ct=
6	LRC	Thay đổi lãi suất cho vay	LRCt =
7	DCRC	Thay đổi lãi suất chiết khấu	DCRCt=
8	DRC	Thay đổi lãi suất tiền gửi	DRCt =

Có thể bạn quan tâm!

Xem toàn bộ 56 trang tài liệu này.

9 Các cổ phiếu ngành bảo hiểm chiếm 6.86% trong tỉ lệ ảnh hưởng của chỉ số Bank index

2.2. Phương pháp nghiên cứu:

2.2.1. Hồi quy OLS và hồi quy có biến giả:

a, Hồi quy OLS:

Giả sử có hàm hồi quy tổng thể (PRF) 2 biến như sau:

Yi = α + β*Xi + ui

Trong đó, Y là biến phụ thuộc, X là biến giải thích (hay biến hồi quy độc lập), u là số hạng nhiễu ngẫu nhiên và i là quan sát thứ i. β0 là số hạng tung độ gốc, cho biết ảnh hưởng trung bình của tất cả các biến bị loại ra khỏi mô hình đối với Y, hay là giá trị trung bình của Y khi X = 0. β1 là hệ số hồi quy, cho biết sự thay đổi giá trị trung bình của Y khi X thay đổi 1 đơn vị.

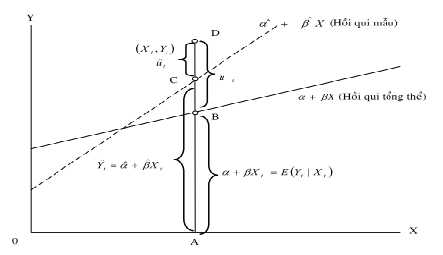
Hình 2.2: Phương trình hồi quy của tổng thể và của mẫu.

Các giả thiết OLS của mô hình hồi quy tuyến tính cổ điển Gauss:

- Mô hình hồi quy là tuyến tính theo tham số của mô hình.

- Biến X là ngẫu nhiên.

- Giá trị trung bình của ui là 0 hay E(ui/X ) = 0

- Không có tương quan chuỗi hay cov (ui,uj) = 0 với i#j

- Phương sai có điều kiện không đổi, hay var (ui) = σ2

- Mô hình được xác định 1 cách đúng đắn (không có độ thiên lệch hay sai số đặc trưng).

Định lý Gauss-Markov: Ước lượng của OLS là ước lượng tuyến tính, không chệch và có phương sai bé nhất (BLUE).

b, Hồi quy phương trình có biến giả:

Trong phân tích hồi quy, biến giả thường được sử dụng cho những biến định tính (là biến thường biểu thị có hay không có một tính chất hoặc các mức độ khác nhau của một tiêu thức thuộc tính nào đó), như: nam hay nữ, sống ở thành thị hay nông thôn, quốc tịch…Những biến định tính này có thể được lượng hóa là 0 hay 1, hoặc từ 1-9.

2.2.2. Tính dừng và kiểm định tính dừng chuỗi thời gian.

2.2.2.1. Chuỗi thời gian và mô hình ARMA: a, Chuỗi thời gian:

Chuỗi thời gian là một chuỗi các giá trị của một đại lượng nào đó được ghi nhận tuần tự theo thời gian. Các giá trị chuỗi thời gian của đại lượng Y được kí hiệu: Y1, Y2, …Yt, … Yn với Yt là giá trị quan sát của Y ở thời điểm t. Dữ liệu chuỗi thời gian phổ biến nhất là dữ liệu tài chính được ghi nhận qua thời gian dài, và thường có số lượng quan sát khá lớn. Ví dụ: Giá đóng cửa của cổ phiếu niêm yết trên sàn HOSE trong 5 năm… Chuỗi thời gian có những đặc điểm cơ bản như: có xu hướng (trend), có tính mùa vụ (seasonal), có tính chu kì (Cyclical), các điểm bất thường (Outliers) và tính ngẫu nhiên. Do đó, khi chúng ta tiến hành hồi quy tuyến tính OLS (bình phương nhỏ nhất) với số liệu chuỗi thời gian thì sẽ vi phạm một số điều kiện bắt buộc và mô hình không có ý nghĩa. Vậy nên, chúng ta phải sử dụng các mô hình ARMA, ARIMA để hồi quy và điều kiện bắt buộc sử dụng mô hình này là chuỗi thời gian phải có “tính dừng”.

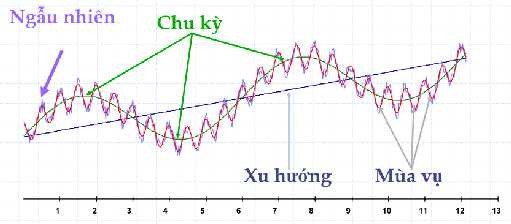
Hình 2.3: Chuỗi thời gian

Một khái niệm quan trọng nữa là “biến trễ” trong phân tích hồi quy liên quan đến chuỗi dữ liệu thời gian. Mô hình hồi quy không chỉ bao gồm giá trị hiện tại mà còn có giá trị quá khứ (giá trị trễ). Mô hình hồi quy có chứa biến giải thích (biến X) là biến trễ, được gọi là mô hình phân phối trễ, còn mô hình chứa biến phụ thuộc ở vế phải phương trình (biến Y) thì gọi là mô hình tự hồi quy. Mô hình có độ trễ càng cao thì càng dễ mất nhiều quan sát, đây là yếu tố cần chú ý khi lựa chọn mô hình.

b, Mô hình ARMA:

Một quá trình ARMA (p, q) sẽ có p số hạng tự hồi quy và q số hạng trung bình trượt

như sau:

Yt=  + [α1Yt -1 +…+ αpYt -p]+ [1Ut-1 +…+ qUt-q ]+ Ut

Mô hình ARMA (p, q) cho thấy biến Y tại thời điểm t không chỉ phụ thuộc vào giá trị quá khứ của nó mà còn phụ thuộc vào sai số quá khứ. Ví dụ, lợi nhuận cổ phiếu thời điểm hiện tại không chỉ phụ thuộc vào lợi nhuận quá khứ mà còn phụ thuộc vào thông tin trên thị trường tại thời điểm t-1, t-2,… t-q.

2.2.2.2. Tính dừng (Stationary): a, Khái niệm:

Một quá trình ngẫu nhiên Yt được coi là dừng nếu kỳ vọng (trung bình), phương sai không đổi theo thời gian và hiệp phương sai giữa hai thời điểm chỉ phụ thuộc vào khoảng cách và độ trễ về thời gian giữa hai thời đoạn này chứ không phụ thuộc vào thời điểm thực tế mà đồng phương sai được tính.

Cụ thể, Yt được gọi là dừng nếu:

- Trung bình: E(Yt) = µ = const (1)

- Phương sai: Var(Yt)= E (Yt –µ)2= σ2 = const (2)

- Đồng phương sai: Cov (Yt-k, Yt) = E [(Yt – µ) (Yt-k – µ)]= γk = const (3)

Quá trình ngẫu nhiên Yt được coi là không dừng nếu nó vi phạm ít nhất một

trong ba điều kiện trên.

b, Cách kiểm định tính dừng:

Tính dừng của chuỗi thời gian có thể được nhận biết dựa trên đồ thị của chuỗi thời gian, đồ thị hàm tự tương quan mẫu hay kiểm định Dickey-Fuller (kiểm nghiệm

đơn vị). Nếu đồ thị Y=f(t) của chuỗi thời gian cho thấy trung bình và phương sai của quá trình Yt không đổi theo thời gian, thì chuỗi thời gian đó có thể có tính dừng.

-Kiểm định Dickey-Fuller (kiểm nghiệm đơn vị- Unit root test):

Phương pháp này được Dickey và Fuller phát hiện vào năm 1979 để kiểm tra một chuỗi thời gian có phải có tính dừng hay không, được sử dụng phổ biến hơn biểu đồ tự tương quan. Chuỗi là bước ngẫu nhiên (Random Walk) hay Yt= α*Yt-1+Ut nếu với α=1 thì chuỗi thời gian không có tính dừng (trong đó Ut là nhiễu trắng).

Để kiểm tra tính dừng của chuỗi thời gian, chúng ta có thể sử dụng phương pháp Augmented Dickey – Fuller (ADF) (1979). Trong đó, 2 kiểm định ADF và PP có giả thuyết Ho là chuỗi thời gian không dừng (có nghiệm đơn vị).

H0: α = 1 (Yt là chuỗi không có tính dừng) H1: α < 1 (Yt là chuỗi có tính dừng).

2.2.3. Mô hình phương sai sai số thay đổi theo thời gian:

2.2.3.1 Mô hình ARCH (AutoRegressive Conditional Heteroshedasticity): a, Mô hình ARCH:

Thuật ngữ heteroshedasticity được giải thích là hiện tượng mô hình có phương sai sai số thay đổi do tác động của môi trường ngoài. Mô hình ARCH do Engle phát triển năm 1982, mô hình này cho rằng phương sai của hạng nhiễu tại thời điểm t phụ thuộc vào các hạng nhiễu bình phương ở các giai đoạn trước. Nói cách khác, mô hình ARCH được xây dựng để lập mô hình và dự báo về phương sai có điều kiện. Engle cho rằng tốt nhất chúng ta nên lập 2 mô hình đồng thời cả về giá trị trung bình và phương sai chuỗi số liệu khi nghi ngờ rằng giá trị phương sai thay đổi theo thời gian.

Mô hình đơn giản như sau:

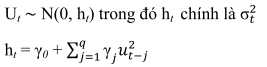
Yt = B1 + B2Xt + Ut (1.1)

(1.2)

Thông thường, ut được giả định có phân phối chuẩn với trung bình bằng 0 và phương sai không đổi là σt2. Theo Engle, phương sai của các hạng nhiễu phụ thuộc vào các giá trị quá khứ, hay phương sai thay đổi theo thời gian. Ở đây, phương trình (1.1)

được gọi là phương trình ước lượng giá trị trung bình và phương trình (1.2) được gọi

là phương trình ước lượng phương sai.

Mô hình ARCH (1) cho rằng khi có một cú sốc lớn ở giai đoạn t-1 thì giá trị ut cũng sẽ lớn hơn.Nghĩa là khi ut-12 biến động bất thường (lớn hay nhỏ) thì phương sai của ut cũng sẽ có biến động tương tự (lớn hay nhỏ). Hệ số ước lượng γ1 phải có dấu dương vì phương sai luôn dương. Thực tế phương sai có điều kiện có thể phụ thuộc không chỉ một độ trễ mà còn nhiều độ trễ trước nó nữa, vì mỗi trường hợp có thể tạo ra một quy trình ARCH khác nhau.

Ví dụ ARCH (2) sẽ được thể hiện như sau:

Yt = B1 + B2Xt-1+ ut

ut ~ N (0, σ 2)

σt2 =γ0 + γ1 ut-12 + γ2 ut-22(1.3) b, Kiểm định tính ARCH:

Trước khi ước lượng các mô hình ARCH (q), điều quan trọng là chúng ta cần kiểm tra xem có tồn tại các ảnh hưởng ARCH hay không (nói cách khác là kiểm tra xem mô hình có phương sai sai số thay đổi không) để biết các mô hình nào cần ước lượng theo phương pháp maximum likelihood thay vì theo phương pháp ước lượng OLS. Kiểm định tính ARCH tương tự như kiểm định Lagrange Multiplier (LM) để kiểm định tự tương quan.

Kiểm định ảnh hưởng ARCH sẽ được thực hiện theo qui trình như sau:

Bước 1:Ước lượng phương trình trung bình theo phương pháp OLS:

Yt = B1 + B2Yt-1 + et (1.4)

Các biến giải thích có thể bao gồm các biến trễ của biến phụ thuộc và các biến giải thích khác có ảnh hưởng đến Yt. Ngoài ra, khi thực hiện với dữ liệu mẫu, thì hạng nhiễu ut trong mô hình (1.4), được đổi thành phần dư et.

Bước 2: Ước lượng phương trình hồi qui phụ sau đây:

e t2 =γ0 + γ1 et-12 + γ2 et-22 +..+ γqet-q2 + wt (1.5)

Sau đó, chúng ta lấy giá trị R2 của mô hình trên.

Bước 3: Xác định giả thiết Ho như sau :

H0: γ0=γ1=γq ( Mô hình không có tính ARCH)

Thống kê này sẽ theo phân phối chi bình phương với số bậc tự do là số độ trễ q (do e t2 trong phương trình hồi quy là một tổng của q thành phần lấy bình phương). Nếu giá trị thống kê chi bình phương tính toán (R2*T) lớn hơn giá trị chi bình phương

phê phán thì chúng ta bác bỏ giả thiết Ho và ngược lại (hay giá trị P-value< 0.05). Nếu bác bỏ giả thiết Ho, thì ta có thể kết luận rằng chuỗi dữ liệu đang xét có ảnh hưởng ARCH.

2.2.3.2. Mô hình GARCH (Generalised Autoregressive Conditional Heteroskedasticity):

Mô hình GARCH được giới thiệu bởi Bollerslev vào năm 1986.Những mô hình này được sử dụng rộng rãi trong các mô hình toán kinh tế, đặc biệt là trong phân tích chuỗi thời gian tài chính giống như Bollerslev, Chou, Kroner đã thực hiện vào năm1992 và Bolleslev, Engle, Nelson đã tiến hành vào năm 1994. Mô hình GARCH (Generalised Autoregressive Conditional Heteroskedasticity) là mô hình tổng quát hóa cao hơn mô hình ARCH.

Mô hình GARCH (p, q) có dạng sau đây:

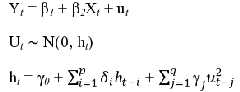
Trong đó: p: là bậc của mô hình GARCH.

q: là bậc của mô hình ARCH

Phương trình (1.6) nói lên rằng phương sai ht bây giờ phụ thuộc vào cả giá trị quá khứ của những thông tin về sự dao động từ thời kì trước (giá trị quá khứ của các cú sốc), được xác định nhờ bình phương phần dư từ phương trình kì vọng, và các giá trị quá khứ của bản thân ht đại diện bởi các biến ht-i. Dạng đơn giản nhất của mô hình GARCH là GARCH(1,1), được biểu diễn như sau:

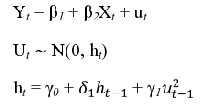
Một ích lợi rõ ràng nhất mô hình GARCH mang lại so với mô hình ARCH là ARCH (q) vô tận = GARCH(1,1). Nếu ARCH có quá nhiều độ trễ (q lớn) thì có thể sẽ ảnh hưởng đến kết quả ước lượng do giảm đáng kể số bậc tự do trong mô hình. Một chuỗi dữ liệu càng nhiều độ trễ sẽ có nhiều biến bị mất. Mô hình này phù hợp khi dữ liệu chuỗi thời gian xuất hiện hiện tượng phương sai của sai số không đồng đều.

-Mô hình GARCH-M:

Mô hình GARCH-M cho phép giá trị trung bình có điều kiện phụ thuộc vào phương sai có điều kiện của chính nó. Nói cách khác, trong tài chính, TSSL của một chứng khoán có thể phụ thuộc vào độ biến động (rủi ro) của chính nó. Ví dụ xem xét hành vi các nhà đầu tư thuộc dạng e ngại rủi ro và vì thế họ có xu hướng đòi hỏi thêm một mức phí bù rủi ro khi quyết định nắm giữ một tài sản rủi ro. Như vậy, phí bù rủi ro là một hàm đồng biến với rủi ro; nghĩa là rủi ro càng cao thì phí bù rủi ro phải càng nhiều. Nếu rủi ro được đo lường bằng mức dao động hay bằng phương sai có điều kiện thì phương sai có điều kiện có thể là một phần trong phương trình trung bình của biến Yt.

Theo cách này, mô hình GARCH-M sẽ có dạng sau:

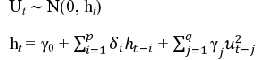
Trên là những kiến thức nền tảng của mô hình ARIMA, ARCH/GARCH. Ưu điểm của mô hình cho ta thấy khả năng ứng dụng rất cao cho công tác dự báo và phân tích rủi ro của các dữ liệu tài chính, đặc biệt là chuỗi dữ liệu của TTCK. Tuy thế giới chỉ mới biết đến và sử dụng mô hình kể từ cuối thế kỉ XX nhưng chỉ vài chục năm với sự hỗ trợ của khoa học công nghệ thông tin ứng dụng, mô hình càng được nhân rộng và phát triển lên một tầm cao mới. Kinh nghiệm sử dụng mô hình ARIMA, ARCH/GARCH trên thế giới trong lĩnh vực chứng khoán sẽ cho ta thấy điều đó.

CHƯƠNG 3: TÌNH HÌNH BIẾN ĐỘNG LÃI SUẤT, TỶ GIÁ VÀ HOẠT ĐỘNG NIÊM YẾT CỦA CỔ PHIẾU NGÂN HÀNG TRÊN TTCK VIỆT NAM

Mặc dù lãi suất tăng cao, doanh nghiệp khó tiếp cận nguồn vốn ngân hàng nhưng nguồn vốn tín dụng vẫn đóng vai trò cung cấp nguồn vốn quan trọng cho doanh nghiệp và là nguồn thu nhập chính cho các ngân hàng thương mại. Bên cạnh đó, tỷ giá hối đoái và sự biến động của nó, đặc biệt là tỷ giá USD/VND không chỉ là mối quan tâm trực tiếp của các doanh nghiệp xuất nhập khẩu, của cơ quan quản lí mà còn nhân tố quan trọng ảnh hưởng lớn đến kết quả kinh doanh của các ngân hàng thương mại. Do đó, để thấy được sự biến động của lãi suất và tỷ giá trong giai đoạn kinh tế phục hồi sau khủng hoảng, tôi sẽ phân tích tình hình của lãi suất và tỷ giá trong thời gian từ năm 2008-2012.

3.1. Tình hình biến động của lãi suất:

Diễn biến lãi suất trong năm 2008 gồm 2 giai đoạn, đó là: cuộc đua tăng lãi suất của các NH vào 6 tháng đầu năm 2008, và một cuộc đua với chiều hướng ngược lại – cuộc đua giảm lãi suất. Sự leo thang của lãi suất qua đêm trên liên ngân hàng với các kỷ lục 20%, 25% liên tục bị đánh đổ, và đỉnh điểm là mức lãi suất 27%/năm…. Có nhiều nguyên nhân khác nhau, đặc biệt mức lạm phát cao 19.39% vào tháng 1 và ảnh hưởng từ cuộc khủng hoảng tài chính ở Mỹ, khiến NH không muốn đẩy mạnh cho vay mà chú trọng đảm bảo an toàn hoạt động. Nhưng nhu cầu vốn của DN cho sản xuất, kinh doanh và đầu tư phát triển thường có kì hạn dài, từ 1 năm trở lên. Bên cạnh đó, sự ấm lên của TTCK và thị trường bất động sản cùng với những đợt sóng trên thị trường vàng đã thu hút nhiều NĐT tham gia.

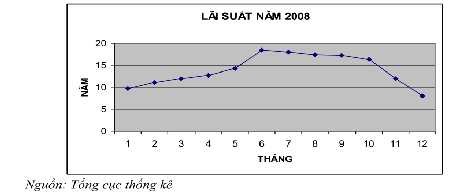
Hình 3.4: Lãi suất huy động vốn năm 2008

Bắt đầu từ tháng 7/2008, các ngân hàng bước vào cuộc đua lãi suất với xu hướng ngược lại với xu hướng 6 tháng đầu năm, do ngân hàng đã giữ được tính thanh khoản của dòng tiền, độ an toàn cao, thu được một nguồn vốn lớn từ 6 tháng trước và tín hiệu tích cực từ lạm phát cùng với sự can thiệp của NHNN.

Năm 2009, lãi suất huy động tăng dần qua các tháng trong năm, cho thấy sự căng thẳng nguồn vốn của các ngân hàng. Tháng 12/2009, lãi suất cho vay sản xuất kinh doanh cao nhất là 12%, nhưng do được hỗ trợ lãi suất nên phần thực trả của doanh nghiệp chỉ 8%/năm. Nguyên nhân là do áp lực về vốn để thực hiện chính sách cho vay ưu đãi của chính phủ và nhu cầu đáo hạn các khoản tiền gửi vào cuối năm. Khi ngân hàng thực hiện chính sách hỗ trợ lãi suất, thì điều kiện là không được từ chối cho vay nếu đối tượng đủ điều kiện.

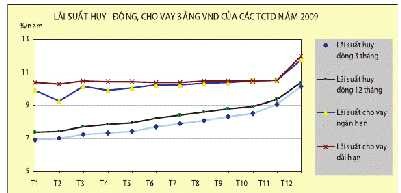
Nguồn: Báo cáo thường niên của NHNN.

Hình 3.5: Lãi suất huy động, cho vay bằng VND của các TCTD năm 2009

Năm 2010, trước những biến động thị trường tiền tệ trong nước cũng như trên thế giới, Chính phủ và NHNN thực hiện điều hành chính sách tiền tệ thận trọng, linh hoạt hơn nhằm tạo điều kiện hỗ trợ tích cực cho thị trường tiền tệ - tín dụng hoạt động ổn định. Trước tiên, TT 13 (TT 19 sửa đổi) ban hành ngày 20/5/2010 và có hiệu lực từ ngày 1/10/2010 quy định việc tăng tỷ lệ an toàn vốn tối thiểu CAR từ 8% lên 9% và tổng số vốn cho vay không vượt quá 80% tổng số vốn huy động được. Đồng thời, thông tư cũng nâng hệ số rủi ro của những khoản cho vay kinh doanh chứng khoán và BĐS lên 250%. Và 23 NHTM buộc phải tăng vốn điều lệ tối thiểu lên 3000 tỷ đồng trong năm 2010. Bên cạnh đó, NHNN cũng đã ban hành TT số 03/2010/TT-NHNN; TT 07/2010/TT-NHNN; TT 12/2010/TT-NHNN cho phép TCTD được thực hiện cho

vay bằng VND theo cơ chế lãi suất thỏa thuận. Trước tình trạng leo thang khó có điểm dừng của lãi suất huy động dưới nhiều hình thức, NHNN đã phải trực tiếp yêu cầu các ngân hàng giảm mặt bằng lãi suất huy động, bao gồm cả khoản chi khuyến mại dưới mọi hình thức, sẽ không vượt quá 14%/năm. Như vậy, mặc dù đã cho phép các ngân hàng được áp dụng lãi suất thỏa thuận nhưng trước việc chạy đua lãi suất, NHNN đã phải can thiệp bằng biện pháp hành chính. Lãi suất cho vay trong năm 2010 thể hiện hai điểm nóng là trong những tháng đầu năm (trước và sau khi thực hiện lãi suất thỏa thuận theo thông tư số 07/2010/TT-NHNN) và hai tháng cuối năm thì lãi suất cho vay ở mức khá cao (khoảng 14.5 – 18%).

Bảng 3.2 : Diễn biến lãi suất điều hành năm 2010 của NHNN

Diễn biến lãi suất điều hành năm 2010 của NHNN

Thời gian

Lãi suất

cơ bản (%)

Lãi suất tái cấp

vốn (%)

Lãi suất tái chiết

khấu (%)

Lãi suất cho vay qua

đêm (%)

1/1 – 4/11/2010

5/11 – 12/2010

Nguồn: Ngân hàng Nhà nước

Trong thời gian trước tháng 3/2011, nền kinh tế nước ta đang trên đà phục hồi nên lãi suất không có nhiều biến động. Tuy nhiên, sau tháng 3, lạm phát bắt đầu tăng nên NHNN phải thực hiện chính sách tiền tệ thắt chặt, điều này làm tăng lãi suất tiền gửi và cho vay ở các NHTM. Nhằm ngăn chặn tính cạnh tranh không lành mạnh giữa các ngân hàng, NHNN ban hành TT 02/2011/TT-NHNN ngày 3/3/2011 quy định về mức lãi suất trần huy động tiền gửi là 14% cho các NHTM. Mặc dù NHNN đã có nhiều biện pháp (ví dụ: sa thải lãnh đạo NH nếu phát hiện thủ thuật gian lận…), nhưng với áp lực rủi ro thanh khoản, các NHTM vẫn tìm mọi cách để “lách luật”. Do đó, NHNN phải bổ sung TT 30/2011/TT-NHNN ngày 28/9/2011, quy định lãi suất tối đa với tiền gửi bằng đồng Việt Nam của tổ chức, cá nhân tại TCTD, chi nhánh ngân hàng nước ngoài, cụ thể: lãi suất tối đa áp dụng với tiền gửi không kì hạn và có kì hạn dưới 1 tháng là 6%/năm. Lãi suất tối đa áp dụng với tiền gửi có kì hạn từ 1 tháng trở lên là

14%/năm, riêng Quỹ tín dụng nhân dân là 14.5%. Quy định trần lãi suất 14%/năm làm cho các NHTM gặp khó về thanh khoản và phải đi vay trên thị trường liên ngân hàng với lãi suất cao. Cá biệt, có những giao dịch lãi suất lên tới mức 30-40%/năm kỳ hạn 1 tháng.

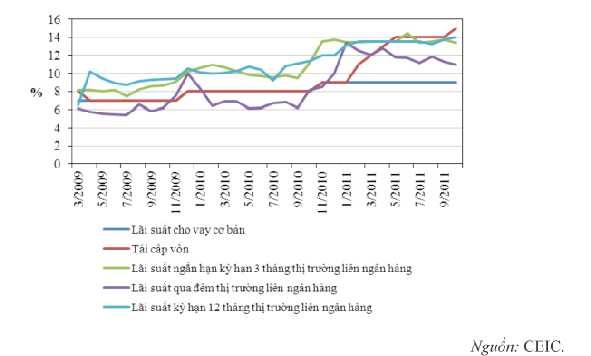
Hình 3.6: Biến động các loại lãi suất trên thị trường liên ngân hàng

NHNN đã liên tục giảm lãi suất nhằm giúp đỡ các doanh nghiệp đang gặp khó khăn khi tiếp cận nguồn vốn vay ngân hàng, cụ thể lãi suất huy động đã được giảm 5 lần từ 14% về còn 8% ở thời điểm cuối năm: lần đầu tiên vào ngày 13/3 theo yêu cầu của Thủ tướng chính phủ lãi suất từ 14% xuống còn 13%; tiếp đó ngày 11/4 giảm 1% về còn 12%; và 28/5/2012 giảm về 11%; ngày 11/6 giảm về 9%. Bên cạnh đó, thông tư 19 NHNN ban hành ngày 8/6/2012 cho phép các NHTM tự quyết định lãi suất kì hạn dài. Lãi suất cho vay trên thị trường liên ngân hàng giảm mạnh xuống mức thấp nhất trong những năm gần đây ở hầu hết các kì hạn, dao động quanh mức 2% với lãi suất qua đêm so với mức trên 20% vào năm 2011. Lãi suất này giảm và ổn định kể từ khi thông tư 21 có hiệu lực, NHNN điều tiết chủ yếu qua nghiệp vụ thị trường mở và phát hành tín phiếu. Lãi suất tín phiếu trên thị trường mở (OMO) đang có xu hướng giảm dần, tạo điều kiện cho lãi suất trái phiếu chính phủ giảm, từ đó định hướng giảm lãi suất chung trên toàn thị trường.

O IR

20029001290020229206042910606290030729200092900170029201122100713212051521201412200211210813220091422051621021822002192210191122001512320120

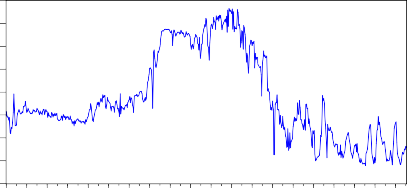
Nguồn: NHNN và kết quả xử lí số liệu bằng Eviews

Hình 3.7: Diễn biến lãi suất qua đêm liên ngân hàng năm 2012.

Biểu đồ cho thấy lãi suất qua đêm liên ngân hàng có xu hướng tăng từ năm 2009 đến năm 9/3/2012, sau đó là đợt giảm mạnh, và biến động cho đến thời điểm 12/3/2013.

G S R 5

20029001290020229206042910606290030729200092900170029201122100713212051521201412200211210813220091422051621021822002192210191122001512320120

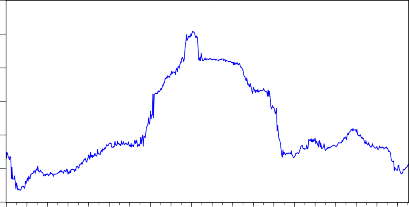
Nguồn: Dữ liệu Bloomberg và kết quả xử lí số liệu bằng Eviews

Hình 3.8: Biến động lãi suất trái phiếu chính phủ 5 năm.

Lãi suất trái phiếu chính phủ 5 năm cũng có xu hướng tăng cho đến tháng 6/2011 rồi giảm dần cho đến thời điểm ngày 12/3/2013.

3.2. Tình hình biến động của tỷ giá hối đoái:

Những năm trước năm 2008, theo Thời báo kinh tế Việt Nam (vneconomy.vn) thì tỷ giá USD/VND thường khá ổn định, bình quân thời kì 2004 2007 tăng 0.57%. Tuy nhiên, bước sang năm 2008 thì biến động tỷ giá có sự biến động khác so với năm trước.

Sự khác nhau này thể hiện qua 4 giai đoạn:

(1) Giảm liên tục trong 3 tháng đầu (1/1/2008-25/3/2008): Đây là giai đoạn kiều hối chuyển về nước khá lớn nên đã hình thành hiện tượng cung lớn hơn cầu, đẩy tỷ giá USD/VND trên thị trường liên ngân hàng liên tục sụt giảm (từ 16,112đ xuống còn 15,960đ, mức thấp nhất là 15,560đ/USD). Đồng thời, chính phủ và NHNN cũng đẩy mạnh kiềm chế lạm phát và thực hiện chính sách tiền tệ thắt chặt. Do đó, NHNN không mua đô la Mỹ nhằm hạn chế bơm tiền vào lưu thông, tăng biên độ tỷ giá từ 0.75% lên 1% trong ngày 10/3/2008.

(2) Tỷ giá tăng mạnh (26/3-16/7/2008) và liên tục, đỉnh điểm vào ngày 18/6 là 19,400đ/USD, chênh lệch 2,600đ so với mức trần và sau đó giảm dần. Ngày 27/6, NHNN tăng biên độ dao động tỷ giá từ 1% lên 2%.

(3) Tỷ giá giảm mạnh và dần đi vào ổn định (17/7-15/10/2008): Với sự can thiệp kịp thời của NHNN, tỷ giá đã giảm xuống mức 16,400 đ/USD, và dao động quanh mức 16,600 từ tháng 8 đến tháng 11. Nhận thấy cơn sốt đô la Mỹ đã ở mức báo động, NHNN đã công khai dự trữ ngoại hối quốc gia lên đến 20.7 tỷ đô la Mỹ khi thông tin trên thị trường cho rằng đô la Mỹ đang khan hiếm. Đồng thời, NHNN cũng ban hành một loạt chính sách nhằm bình ổn thị trường, như: cấm mua bán ngoại tệ trên thị trường tự do, cấm mua bán USD thông qua đồng tiền khác để lách biên độ,…

(4) Tỷ giá tăng đột ngột trở lại, đạt mức 16,998 đ/USD. Sau khi NHNN tăng biên độ tỷ giá từ 2% lên 3% trong ngày 7/11/2008, tỷ giá đã tăng tới mức 17,440đ/USD.

Năm 2009, tỷ giá USD/VND liên tục tăng mạnh, ở các NHTM tỷ giá niêm yết mua và bán luôn ở mức sát trần. Do đó, từ ngày 26/11/2009, NHNN đã tiến hành tăng tỷ giá bình quân liên ngân hàng lên mức 17,961 đ/USD (quyết định phá giá VND 5.4%, tỷ lệ phá giá cao nhất từ năm 1998 để chống đầu cơ tiền tệ) và biên độ tỷ giá +/- 3% sẽ được thay thế cho biên độ +/- 5% như trước đây. Ngoài ra, Thủ tướng yêu cầu các tập đoàn, tổng công ty lớn Nhà nước phải bán ngoại tệ đang nắm giữ cho ngân hàng. Đồng thời, 8