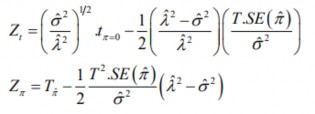Mô Hình Ảnh Hưởng Của Fdi Từ Thiên Đường Thuế Đến Xói Mòn Cơ Sở Thuế

TRADE: Độ mở thương mại của mỗi quốc gia

εit : phần dư của mô hình với εit ≈ i.i.d (0, бi2), E(μi/εit) = 0 i =1, 2, 3, …, N

t = 1, 2, 3, …, T

(N và T lần lượt là số quốc gia và khoảng thời gian quan sát trong mô hình)

Phương trình xem xét hiệu ứng phi tuyến của thuế suất luật định với FDI mở rộng từ phương trình (3.2) và trở thành:

LGFDIi,t = β0 + β1RTAXINCi,t + β2RTAXINC3i,t + β3GDPi,t + β4POPULAi,t

+ β5INFLATi,t + β6GOSPENi,t + β7PROPRI i,t + εi,t

Phương trình xem xét hiệu ứng phi tuyến của thuế suất hiệu quả với FDI mở rộng từ phương trình (3.3) và trở thành:

LGFDIi,t = β0 + β1TAXPROi,t + β2TAXPRO3i,t + β3GDPi,t + β4POPULAi,t

+ β5INFLATi,t + β6GOSPENi,t + β7PROPRI i,t + εi,t

Có thể bạn quan tâm!

Xem toàn bộ 193 trang tài liệu này.

Hiệu ứng phi tuyến sẽ tồn tại khi mà dấu kỳ vọng của β1 và β2 là ngược chiều nhau, hay có sự đổi dấu của β1 và β2. Dấu kỳ vọng của của β1 và β2 thể hiện mối quan hệ phi tuyến giữa thuế suất thuế TNDN và FDI. Trên đồ thị thể hiện sự phi tuyến này sẽ tồn tại một giá trị xác định của thuế suất làm cho tác động của nó lên FDI bằng 0. Giá trị xác định này được xem là ngưỡng của thuế suất trong hiệu ứng phi tuyến. Do đó, thuế suất TNDN trước giá trị ngưỡng và sau giá trị ngưỡng sẽ tác động ngược chiều nhau. Vì vậy, nếu có hiệu ứng phi tuyến xảy ra, nghĩa là theo chính sách cạnh tranh thuế, trong giai đoạn đầu khi các quốc gia chỉ tập trung biện pháp sử dụng thuế suất, một sự gia tăng trong thuế suất thuế TNDN sẽ làm giảm FDI, và sẽ tiếp tục giảm cho đến đạt một mức ngưỡng. Nhưng sau đó, khi các chính sách thuế được cải cách tốt hơn, sự tăng lên trong thuế suất thuế TNDN sẽ làm tăng FDI. Luận án sử dụng phương pháp ước lượng GLS để xác định độ lớn của các hệ số hồi quy và phương pháp 2SLS để kiểm tra tính vững cho mô hình.

3.3.2 Mô hình ảnh hưởng của FDI từ thiên đường thuế đến xói mòn cơ sở thuế

Luận án tiếp tục tiến hành nghiên cứu thực nghiệm ảnh hưởng của FDI đến thuế TNDN của các quốc gia đang phát triển, sau khi chứng minh mối quan hệ nhân quả giữa thuế TNDN và FDI bằng phương pháp định lượng.

Ảnh hưởng của FDI đến thuế TNDN của các quốc gia đang phát triển được phân tích qua mô hình về xói mòn cơ sỏ thuế TNDN do FDI từ các thiên đường thuế gây ra, được đề xuất bởi Richard Bolwijn, Bruno Casella and Davide Rigo (2018) và Petr Janský và Miroslav Palanský (2019).

RINCOMEi,t = α+ β1RINCOMEi,t-1 + 𝛃2RHAVEi,t + ∑ 𝑋 i,t + εi,t (3.5)

Do mối quan hệ nhân quả giữa thuế và FDI, phương trình (3.5) là mô hình động với sự hiện diện của biến trễ RINCOMEit-1. Trong đó:

RINCOMEit: là thu nhập của dòng FDI vào các quốc gia đang phát triển, được tính bằng tỷ suất lợi nhuận của FDI trên dòng FDI vào của mỗi quốc gia. Đây cũng là biến đại diện cho cơ sở thuế TNDN.

RHAVEit: là tỷ trọng của dòng FDI từ các thiên đường thuế vào các quốc gia đang phát triển, được tính bằng tỷ lệ của FDI từ thiên đường thuế trên tổng dòng FDI vào của mỗi quốc gia.

 Xit: tập hợp các biến kiểm soát trong mô hình, gồm: GDP: tốc độ tăng trưởng kinh tế hàng năm tính theo tỷ lệ %

LABOR: số người trong độ tuổi lao động của mỗi quốc gia, dưới dạng logarit POPULA: tổng dân số của mỗi quốc gia, dưới dạng logarit

INFLAT: tỷ lệ lạm phát hàng năm của mỗi quốc gia và được tính theo tỷ lệ % PROPRI: chỉ số quyền tài sản của mỗi quốc gia

GOINTEG: chỉ số minh bạch của mỗi quốc gia

εit : phần dư của mô hình với εit ≈ i.i.d (0, бi2), E(μi/εit) = 0 i =1, 2, 3, …, N

t = 1, 2, 3, …, T

(N và T lần lượt là số quốc gia và khoảng thời gian quan sát trong mô hình);

3.4 Phương pháp nghiên cứu

3.4.1 Phương pháp ước lượng bình phương tối thiểu tổng quát (GLS)

Giả thuyết quan trọng trong mô hình hồi quy tuyến tính cổ điển là các yếu tố sai số xuất hiện trong hàm hồi quy tổng thể có phương sai không thay đổi, nghĩa là chúng có cùng phương sai; đồng thời không có quan hệ tương quan chuỗi giữa các sai số, nghĩa là không có hiện tượng tự tương quan. Khi các giả thuyết này bị vi phạm, hiện tượng phương sai thay đổi và tự tương quan sẽ khiến cho các hệ số hồi quy ước lượng

được bằng phương pháp bình phương nhỏ nhất dù vẫn tuyến tính và không thiên lệch, nhưng không còn là ước lượng hiệu quả nhất. Tuy nhiên, Moulton (1986) và Moulton (1990) cho rằng khi sử dụng dữ liệu bảng để phân tích có thể gặp phải sự hiện diện của hiệu ứng nhóm dẫn tới vấn đề sai số trong các kết luận thống kê.

Khắc phục những nhược điểm này, phương pháp GLS (generalized least squares) được đặt dưới giả định rằng mô hình là hoàn toàn xác định, có sự khác biệt về phương sai sai số ở mỗi nhóm đối tượng, nhưng là không đổi trong phạm vi từng đối tượng. Với những giả thuyết này, GLS đem lại ước lượng tiệm cận hiệu quả và vững. Đồng thời, việc ước lượng cũng cho phép khắc phục hiện tượng tự tương quan và phương sai thay đổi trong mô hình hồi quy với dữ liệu bảng. Vì vậy, Scot & Holt (1982) đề xuất sử dụng phương pháp bình phương tối thiểu tổng quát (GLS) sẽ ít bị thiên chệch hơn trong các sai số chuẩn dùng để ước lượng các hệ số góc.

Trường hợp bỏ qua hiệu ứng nhóm, uớc lượng OLS và sai số chuẩn không điều chỉnh được tính theo công thức:

𝛽̂ = (𝑋′𝑋) −1𝑋′𝑦, 𝑣𝑎𝑟 ̂ (𝛽̂) = 𝑠 2 (𝑋 ′𝑋) −1

𝑠 2 = 𝑦′(𝑦 − 𝑋𝛽̂)/(𝑛 − 𝑘)

Moulton (1986) đề xuất sử dụng phương pháp kiểm định nhân tử Lagrange để kiểm tra sự hiện diện của hiệu ứng nhóm. Khi đó, ước lượng GLS được dùng để tính các sai số chuẩn gần đúng bằng phương pháp maximum likelihood:

𝛽̃ = (𝑋 ′𝑉̃ −1𝑋) −1𝑋 ′𝑉̃ −1𝑦, 𝑣𝑎𝑟 ̃ (𝛽̃) = (𝑋 ′𝑉̃ −1𝑋) −1

Trong đó 𝑉̃ được tính tại các ước lượng của thành phần phương sai hoặc hiệp phương sai. Cuối cùng, sai số chuẩn điều chỉnh OLS được tính theo công thức:

𝑣𝑎𝑟 ̃ (𝛽̂) = (𝑋 ′𝑋) −1𝑋′𝑉̃𝑋 (𝑋 ′𝑋) −1

Mô hình chuyển đổi cuối cùng lúc này thỏa mãn các giả thuyết của mô hình cổ điển, không có phương sai thay đổi và tự tương quan. Do đó, áp dụng phương pháp OLS trên mô hình này sẽ thu được ước lượng vững, hiệu quả và không chệch.

3.4.2 Ước lượng với biến công cụ

Các mô hình nghiên cứu trước đây về tác động của thuế TNDN đến FDI đều có khả năng xảy ra hiện tượng nội sinh do mối quan hệ tương hỗ giữa các biến vĩ mô trong mô hình. Để khắc phục tính thiên chệch của ước lượng do hiện tượng nội sinh gây ra, tác giả sử dụng phương pháp ước lượng với biến công cụ bằng phương pháp bình

phương tối thiểu hai giai đoạn (2SLS) nhằm kiểm tra tính vững cho mối quan hệ này. Phương pháp này được Bollen (1995, 1996) đề xuất và phát triển. Các nghiên cứu thực nghiệm của Li & Harmer (1998), Oczkowski & Farrell (1998), Farrell (2000), Oczkowski (2001), Farrell & Oczkowski (2002), và Smith & ctg (2002, 2003) cho thấy sử dụng 2SLS cho thấy kết quả ước lượng giảm tính thiên chệch so với các ước lượng truyền thống.

Để kiểm tra mô hình có bị nội sinh và việc sử dụng ước lượng 2SLS là cần thiết, tác giả dựa vào đề xuất của Davidson & MacKinnon (1993) cho dữ liệu bảng. Ngoài ra, kiểm định Sagan-Hansen cũng được sử dụng để đánh giá việc sử dụng các biến làm biến công cụ cho thu nhập có thỏa mãn ràng buộc nhận dạng quá mức (overidentifying restriction).

3.4.3 Ước lượng GMM Arellano-Bond sai phân hai bước

Theo các nghiên cứu thực nghiệm trước đây, các mô hình cơ bản để xem xét mối quan hệ giữa thuế TNDN và FDI thường bắt đầu bằng mô hình hồi quy cơ bản Pool ước lượng bình phương bé nhất (OLS). Tuy nhiên, do các giả định mạnh của OLS thường khó thỏa mãn trong thực tế, nên mô hình này có thể phản ánh sai hệ số hồi quy của X đối với Y. Mô hình Pool không còn phù hợp do vi phạm các giả thuyết quan trọng như:

(1) Hiện tượng nội sinh trong mô hình: Một trong những giả thuyết quan trọng để phương pháp OLS cho kết quả tốt nếu các biến trong mô hình không có hiện tượng nội sinh. Tuy nhiên trong thực tế, các biến đại diện cho thuế TNDN, FDI, và các biến kinh tế vĩ mô liên quan thường tác động qua lại lẫn nhau hoặc xuất hiện những nhân tố tác động đông thời… nên có thể sẽ dẫn đến hiện tượng nội sinh do có mối quan hệ hai chiều giữa hai biến. Đối với mối quan hệ giữa thuế TNDN và FDI, bằng các nghiên cứu thực nghiệm, các nhà kinh tế học đã tìm ra được một mối quan hệ nội sinh giữa thuế và đầu tư trực tiếp nước ngoài. Trong đó, thuế TNDN có tác động trực tiếp đến dòng FDI của các quốc gia, và ngược lại, dòng vốn FDI cũng ảnh hưởng đến thuế TNDN của các quốc gia đó với các mức độ khác nhau.

(2) Phương sai thay đổi: Một số đặc điểm mang tính chất quốc gia, bất biến không thay đổi theo thời gian (hay còn gọi là hiệu ứng cố định) liên quan đến FDI như nhân chủng học, đặc điểm văn hóa, khoảng cách địa lý… có thể hiện hữu mối tương quan với những biến giải thích. Những tác động cố định này là hiện diện trong đại lượng

sai số µi của những phương trình thực nghiệm… khiến vi phạm giả thuyết mô hình Pool.

(3) Hiện tượng tự tương quan: các biến đại diện cho thuế TNDN, FDI, và các biến kinh tế vĩ mô được thu thập là dữ liệu chuỗi thời gian, hơn nữa trong thực tế các biến này sẽ có sự tác động qua lại theo độ trễ của thời gian (ví dụ dòng vốn FDI năm nay bị tác động bởi dòng FDI năm ngoái và những năm trước…). Do đó, nếu có hiện tượng tự tương quan (hoặc tương quan chuỗi), thì các sai số chuẩn ước lượng, và tự bản thân nó, các giá trị t ước lượng sẽ bị nghi ngờ. Vì thế, trước khi chúng ta chấp nhận các kết quả của mô hình Pool, chúng ta cần kiểm tra xem có sự hiện diện của hiện tượng tự tương quan hay không.

Những vấn đề này dẫn đến hiện tượng ước lượng không nhất quán và bị chệch bởi phương pháp hồi qui OLS. Vì vậy, luận án nghiên cứu áp dụng kỹ thuật hồi qui moment tổng quát GMM Arellano & Bond (1991) do Holtz-Eakin & ctg (1988) đề xuất. Để loại bỏ những tác động cố định được đề cập trên (fixed effects), trong những hồi qui này, tất cả những biến sử dụng dưới dạng sai phân bậc một. Ngoài ra, theo Judson & Owen (1999), một số biến có tính nội sinh được dùng như biến được công cụ dưới dạng các độ trễ khác nhau trong khi các biến có tính ngoại sinh còn lại sẽ được sử dụng như biến công cụ với giả thuyết rằng các sai số ở phương trình gốc không tồn tại hiện tượng tương quan chuỗi nghiêm trọng. Ước lượng GMM sử dụng các điều kiện moment cho phép tạo ra các ước lượng chính xác ngay cả khi có sự xuất hiện của sự không nhất quán của các đơn vị chéo (Hansen, 2000; Hayashi, 2000).

Để kiểm tra tính vững của ước lượng, nghiên cứu sử dụng phương pháp Difference GMM được phát triển cho mô hình bảng động tuyến tính (Arellano & Bond, 1991; Arellano & Bover, 1995; Holtz-Eakin, 1988). Theo GMM, phương trình ước lượng sẽ được biến đổi thành phương trình sai phân có dạng:

∆𝑦𝑖𝑡 = 𝛾∆𝑦𝑖𝑡−1 + 𝛽∆𝑋𝑖𝑡 + 𝛿∆𝑍𝑖𝑡 + ∆𝑢𝑖𝑡

Với ∆ là toán tử sai phân bậc 1

Khi chuyển sang hồi quy với biến sai phân bậc 1, các thiên chệch tiềm ẩn do bỏ sót biến và các hiệu ứng cố định của các đơn vị chéo (địa lí, nhân khẩu học) sẽ được loại bỏ. Tuy nhiên, sai phân hóa làm cho ∆𝑦𝑖𝑡−1 tương quan với ∆𝑢𝑖𝑡 và khiến các ước lượng của mô hình bị chệch. Khi đó, ước lượng GMM sai phân sẽ xử lý được vấn đề này bằng

cách lấy giá trị trễ của các biến phụ thuộc làm công cụ. Arellano & Bond (1991) đề xuất sử dụng các đỗ trễ từ 𝑦𝑖𝑡−2 làm biến công cụ cho ∆𝑦𝑖𝑡−1 vì 𝑦𝑖𝑡−2 có tương quan với 82

∆𝑦𝑖𝑡−1 nhưng không tương quan với ∆𝑢𝑖𝑡, trong điều kiện 𝑢𝑖𝑡 không bị tương quan chuỗi.

Ta có : 𝐸| 𝑌 𝑖,𝑡−𝑠∆𝑢𝑖𝑡 | = 0 với t=3,4,…,T và 𝑠 ≥ 2

Mặt khác, giả định ngoại sinh hoàn toàn của các biến giải thích không còn đúng trong trường hợp có hiện tương nhân quả ngược (𝐸| 𝑌 𝑖,𝑡−𝑠𝑢𝑖𝑡 | ≠ 0 với 𝑡 < 𝑠). Vì vậy, đối với các biến giải thích bị nội sinh yếu hay được xác định trước thì chỉ có các độ trễ của nó mới phù hợp làm biến công cụ:

𝐸| 𝑌 𝑖,𝑡−𝑠∆𝑢𝑖𝑡 | = 0 với t=3,4,…,T và 𝑠 ≥ 2

Với các giả định trên, phương trình có thể được ước lượng với GMM. Cuối cùng, Jodson &ctg (1996) và Roodman (2006) cho rằng GMM sai phân thích hợp cho dữ liệu bảng với T nhỏ và N lớn.

Liên quan đến tính hiệu quả trong việc hồi qui thì các ước lượng GMM sai phân hai bước (dif-GMM) hiệu quả hơn nhiều so với các ước lượng GMM sai phân một bước. Tuy vậy, Roodman (2009) cho rằng việc áp dụng dif-GMM trong các mẫu nhỏ, như trong nghiên cứu này chẳng hạn, cũng gặp phải một số vấn đề khác mà có thể khiến cho việc ước lượng không đạt tối ưu. Điều này nảy sinh do sự xuất hiện quá nhiều các biến được sử dụng làm biến công cụ, gia tăng nếu mà khoảng thời gian quan sát trong mẫu nghiên cứu tăng lên. Do vậy, số lượng biến công cụ hình thành tương đối lớn so với số lượng các nước. Để tránh điều này, Roodman (2009) đề xuất áp dụng quy tắc ngón trỏ sao cho số lượng biến công cụ nhỏ hơn hoặc bằng số lượng các nước trong mẫu nghiên cứu.

Tính hợp lý của các biến được dùng như biến công cụ trong dif-GMM được đánh giá thông qua các thống kê Arellano-Bond và thống kê Sargan/ Hansen. Kiểm định Arellano-Bond được dùng để dò và phát hiện tự tương quan chuỗi ở sai phân bậc một. Do vậy, kết quả kiểm định tương quan chuỗi bậc một AR(1) không cần được quan tâm, trong khi tự tương quan chuỗi bậc hai AR(2) được kiểm định dựa trên chuỗi sai phân bậc 1 của sai số để phát hiện hiện tượng tự tương quan bậc một của sai số. Trong khi đó, kiểm định Sargan/Hansen với giả thuyết null H0: biến công cụ có tính ngoại sinh, nghĩa là biến công cụ không tương quan với sai số. Vì thế, p-value của thống kê Hansen/Sargan càng lớn càng tốt.

3.4.4 Kiểm định quan hệ nhân quả giữa thuế thu nhập doanh nghiệp và FDI

Lý thuyết và các kết quả nghiên cứu thực nghiệm trên cho thấy rằng, thuế TNDN và FDI đã có mối quan hệ hai chiều tùy thuộc vào dữ liệu nghiên cứu và các giai đoạn nghiên cứu khác nhau. Do đó, trước khi xem xét ảnh hưởng của FDI đến thuế TNDN trong mẫu nghiên cứu, cần thiết phải đánh giá mối quan hệ nhân quả Granger giữa hai biến này trước khi tiến hành hồi qui.

Quan hệ nhân quả Granger giữa thuế TNDN và FDI được kiểm định cho mối quan hệ giữa các biến:

(iii) Mối quan hệ giữa số thu thuế TNDN và dòng FDI vào các quốc gia đang phát triển.

(iv) Mối quan hệ giữa cơ sở thuế TNDN và dòng FDI từ thiên đường thuế vào các quốc gia đang phát triển.

Các kiểm định được thực hiện thông qua áp dụng các kiểm định đồng nhất về sự phụ thuộc giữa các quốc gia, tính dừng, đồng liên kết, và kiểm định mối quan hệ nhân quả.

3.4.4.1 Kiểm định giả thuyết về sự phụ thuộc giữa các quan sát chéo trong dữ liệu bảng (Cross-Sectional Dependence – CD Test)

Kiểm định được thực hiện trước tiên để xác định việc tồn tại mối quan hệ giữa các quốc gia trong khu vực (Urbain & Westerlund, 2006). Bên cạnh đó, vì dữ liệu bảng trong nghiên cứu có số quan sát chéo lớn hơn số quan sát về thời gian (N =32 và T =11), thống kê nhân tử Lagarane thông qua các thống kê Pesaran (2004), Friedman (1937) và Frees (1995) được sử dụng do sự phù hợp của nó với bối cảnh T < N (Hoyos & Sarafidis, 2006; Blackburne & Frank, 2007) trong quá trình kiểm tra sự phụ thuộc giữa các quốc gia.

3.4.4.2 Kiểm định tính dừng của các biến

Do kiểm định nhân quả Granger yêu cầu các chuỗi dừng, nên các biến tham gia sẽ được kiểm định tính dừng cho dữ liệu bảng. Tác giả kiểm tra tính dừng của các biến theo các kiểm định Augmented Dickey Fuller (ADF), Phillips-Perron (PP) và Im- Pesaran-Shin (IPS). Giả thuyết H0 của kiểm định này là tồn tại nghiệm đơn vị, có nghĩa là các biến không dừng.

 Kiểm định Augmented Dickey Fuller (ADF)

Dựa trên nền tảng kiểm định Dickey-Fuller, ADF có mô hình như sau:

Trong đó: Yt : Biến chuỗi thời gian cần khảo sát.

∆ : toán hạn sai phân

b; a0; …am : các tham số ước lượng ut : nhiễu trắng

Giả thuyết null trong các tình huống này có thể được diễn đạt:

H0: β = 0 (cho thấy Yt có một xu hướng stochastic, đó là không dừng). Giả thuyết đối lập: H1: β ≠ 0 (cho thấy Yt dừng)

Một xu thế thời gian (t) có thể được thêm vào phương trình trên, nếu Yt dừng quanh một quá trình tuyến tính xác định. Vì thế, phương trình trên được xác định lại:

với, t: là biến xu thế; và δ: là tham số ước lượng của biến xu thế.

 Kiểm định Philips-Perron Phillips và Perron:

Philips-Perron Phillips và Perron đã phát triển một loạt các kiểm định nghiệm đơn vị, sau này trở nên phổ biến cho phân tích chuỗi thời gian trong tài chính. Các kiểm định nghiệm đơn vị Phillips-Perron (PP) khác với các kiểm định ADF chủ yếu theo cách mà chúng xử lý đối với tương quan chuỗi và phương sai sai số không đồng nhất. Đặc biệt, trong khi ADF sử dụng mô hình tự hồi qui kiểu tham số để xấp xỉ cấu trúc ARMA của các sai số trong mô hình kiểm định thì kiểm định PP bỏ qua bất kỳ sự tương quan chuỗi nào trong mô hình kiểm định.

Với Ut tích hợp bậc zero I(0) và có phương sai sai số đồng nhất. Kiểm định PP hiệu chỉnh sự tương quan chuỗi và phương sai sai số không đồng nhất trong các sai số Ut của mô hình kiểm định bằng cách bổ sung trực tiếp các thống kê kiểm định tπ=0 và

𝑇π̂ Các thống kê bổ sung này ký hiệu là Zt và Zπ có dạng: