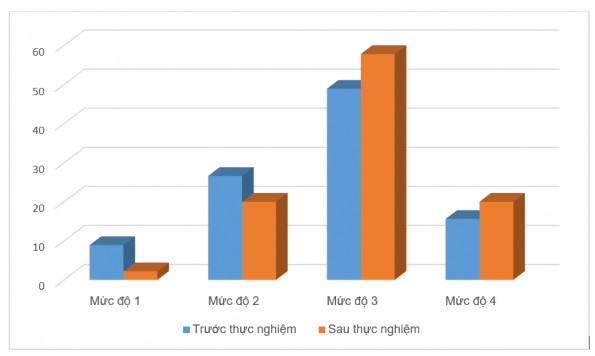
Biểu đồ 3.2 tỉ lệ phần trăm kết quả trước và sau thực nghiệm của lớp đối chứng
Nhận xét: Kết quả kiểm tra trước và sau thực nghiệm của lớp đối chứng không có sự thay đổi lớn.
Bảng 3.5. So sánh kết quả trước và sau của lớp thực nghiệm
Số HS | Mức độ 1 | Mức độ 2 | Mức độ 3 | Mức độ 4 | |||||
SL | % | SL | % | SL | % | SL | % | ||
TTN | 45 | 5 | 11,1 | 19 | 42,2 | 14 | 31,1 | 7 | 15,6 |
STN | 45 | 0 | 0 | 3 | 6,7 | 25 | 55,6 | 17 | 40,7 |
Có thể bạn quan tâm!
-
Biện Pháp 3: Phát Triển Khả Năng Tư Duy, Dự Đoán Phát Hiện, Định Hướng Lời Giải Các Bài Toán Hình Học Lớp 9 -
Biện Pháp 4: Cung Cấp Cho Hs Các Tri Thức Về Các Quy Tắc Suy Luận Lôgic Trong Hình Học 9 -
Phân Tích Chất Lượng Học Sinh Trước Khi Tiến Hành Thực Nghiệm -
Kiến Thức: Hs Hiểu Được Góc Có Đỉnh Ở Bên Trong Đường Tròn, Góc Có Đỉnh Ở Bên Ngoài Đường Tròn. -
Kĩ Năng: Học Sinh Rèn Kĩ Năng Vẽ Cung Chứa Góc Dựng Trên Đoạn Thẳng Cho Trước. -
Kiến Thức: - Học Sinh Hiểu Định Nghĩa Tứ Giác Nội Tiếp, Tính Chất Về Góc Của Tứ Giác
Xem toàn bộ 143 trang tài liệu này.
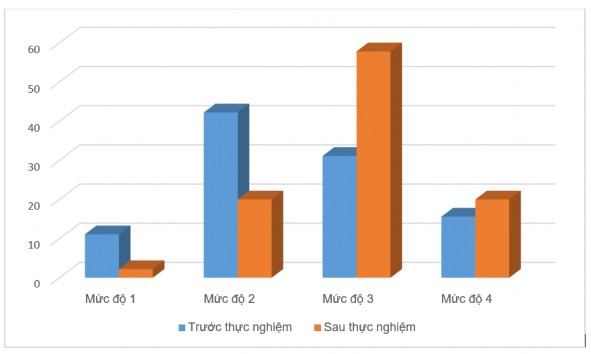
Biểu đồ 3.3 Tỉ lệ phần trăm kết quả trước và sau thực nghiệm của lớp thực nghiệm
Nhận xét: Ta thấy tỉ lệ HS đạt mức 2,3 tăng lên đáng kể, mức độ 0,1 giảm rò rệt. Kết quả trên cho thấy việc phát triển năng lực suy luận cho HS trong quá trình dạy học môn Toán là rất cần thiết.
Qua các biểu đồ trên ta thấy HS các lớp thực nghiệm có năng lực suy luận cao hơn HS lớp đối chứng. Các mức độ điểm số cho thấy rằng năng lực của lớp thực nghiệm tốt hơn lớp đối chứng khá nhiều. Năng lực suy luận của lớp thực nghiệm tiến bộ rò rệt trước và sau thực nghiệm. Như vậy tính khả thi của quan điểm đã được khẳng định.
3.5. Kết luận chương 3
Chương 3 của luận văn đã trình bày quá trình thực nghiệm sư phạm để kiểm chứng tính khả thi và tính hiệu quả của các biện pháp đã trình bày ở chương 2. Quá trình thực nghiệm cùng những kết quả được rút ra từ thực nghiệm cho phép khẳng định: mục đích thực nghiệm đã được hoàn thành, tính khả thi của các quan điểm đã được khẳng định. Thực hiện các quan điểm đó sẽ góp phần phát triển năng lực suy luận trong Toán học nói chung, trong Hình học lớp 9 nói riêng; góp phần phòng tránh tiếp thu kiến thức một cách thụ động, thiếu sáng tạo.
KẾT LUẬN CHUNG
Sau khi hoàn thành nghiên cứu đề tài: “Sử dụng biểu diễn trực quan phát triển năng lực suy luận toán học cho học sinh thông qua dạy học hình học lớp 9 ” chúng tôi rút ra được những kết luận sau:
1. Góp phần làm sáng tỏ cơ sở lý luận và thực tiễn trong việc sử dụng BDTQ phát triển năng lực suy luận cho HS; hệ thống hóa quan điểm của nhiều nhà khoa học về suy luận suy diễn, quy nạp và ngoại suy;
- Tổng hợp và phân tích có hệ thống các khía cạnh lý luận liên quan đến nghiên cứu quá trình suy luận của học sinh. Học sinh cǜng gặp các khó khăn trong quá trình suy luận bởi vì các phát biểu hay các khẳng định mà học sinh đưa ra chỉ dựa trên việc quan sát thực tế từ các hình vẽ tĩnh (bằng giấy và bút). Việc sử dụng BDTQ giúp HS quan sát được trực quan hơn, từ đó giúp HS phát triển khả năng suy luận.
- Hệ thống hóa lý luận về năng lực suy luận.
- Đánh giá thực trạng dạy học hình học 9 ở trường THCS.
2. Đưa ra vai trò của việc sử dụng BDTQ giúp phát triển năng lực suy luận rút ra từ thực nghiệm của các nhóm HS.
3. Đề xuất 4 biện pháp sư phạm nhằm phát triển năng lực suy luận cho HS trong
dạy học hình học 9:
- Biện pháp 1: sử dụng biểu diễn trực quan động hỗ trợ suy luận;
- Biện pháp 2: Xây dựng bài toán hình học kết thúc mở hỗ trợ HS phát triển khả năng khám phá toán bằng suy luận thông qua việc sử dụng BDTQ.
- Biện pháp 3: Phát triển khả năng tư duy, dự đoán phát hiện, định hướng lời giải các bài toán Hình học lớp 9
- Biện pháp 4: Cung cấp cho HS các tri thức về các quy tắc suy luận lôgic trong hình học 9
Trong mỗi biện pháp, tác giả trình bày cơ sở của biện pháp, cách thức thực hiện và minh họa bằng một số ví dụ cụ thể.
4. Luận văn đã thể hiện việc thực nghiệm sư phạm trên đối tượng HS đại trà và
cho thấy kết quả tốt trên các mẫu phiếu học tập. Tuy nhiên, trong quá trình nghiên cứu
không tránh khỏi những thiếu sót. Rất mong nhận được sự đóng góp ý kiến của các quý
thầy cô và các bạn đồng nghiệp để luận văn hoàn thiện hơn
Như vậy, có thể khẳng định: Mục đích nghiên cứu đã được thực hiện, nhiệm vụ nghiên cứu đã được hoàn thành và giả thuyết khoa học là chấp nhận được.
CÔNG TRÌNH KHOA HỌC ĐÃ CÔNG BỐ LIÊN QUAN ĐẾN LUẬN VĂN
Nguyễn Danh Nam, Nguyễn Thị Diệu Ngọc (2021). Sử dụng biểu diễn trực quan động hỗ trợ học sinh suy luận toán học. Tạp chí Giáo dục và Xã hội, ISSN 1859-3917, số 123(184), tr.38-43.
TÀI LIỆU THAM KHẢO
A. Tiếng Việt
1 Ban chấp hành Trung ương khóa XI (2013), Nghị quyết hội nghị Trung ương 8 khóa XI (Nghị quyết số 29-NQ/TW ngày 4-11-2013) về đổi mới căn bản, toàn diện giáo dục và đào tạo.
1 Bộ Giáo dục và Đào tạo (2007), Tài liệu bồi dưỡng phương pháp dạy học,
Dự án phát triển giáo dục Trung học phổ thông.
2 Bộ Giáo dục và Đào tạo (2007), Sách giáo khoa Toán 9 tập 1, Nxb Giáo dục Việt Nam.
3 Bộ Giáo dục và Đào tạo (2007), Sách giáo khoa Toán 9 tập 2, Nxb Giáo dục Việt Nam.
4 Bộ Giáo dục và Đào tạo (2007), Sách Bài tập Toán 9 tập 1, Nxb Giáo dục Việt Nam.
5 Bộ Giáo dục và Đào tạo (2007), Sách Bài tập Toán 9 tập 2, Nxb Giáo dục Việt Nam.
6 Bộ Giáo dục và Đào tạo (2007), Sách GV Toán 9 tập 2, Nxb Giáo dục Việt
Nam.
7 Bộ Giáo dục và Đào tạo (2007), Sách GV Toán 9 tập 2, Nxb Giáo dục Việt
Nam.
8 Bộ Giáo dục và Đào tạo (2017), Dự thảo Chương trình giáo dục phổ thông tổng thể.
10 Cruchetxki V. A (1973), Tâm lí năng lực Toán học của HS, Nhà xuất bản Giáo dục, Hà Nội.
11 Cruchetxki V. A (1980), Những cơ sở Tâm lý học sư phạm, Tập 1, Nhà xuất bản Giáo dục, Hà Nội.
12 Phạm Minh Hạc (1992), Một số vấn đề tâm lí học, Nhà xuất bản Giáo dục, Hà Nội.
13 Đỗ Văn Hùng, Chẩn đoán một số sai lầm của HS tiểu học khi sử dụng phép suy luận tương tự trong học Toán, Education Sci.2012, vol 57, No 9, pp 59- 67.
14 Nguyễn Thị Hương, Phát triển năng lực suy luận ngoại suy cho học sinh trong dạy học hình học lớp 9, Luận án thạc sĩ khoa học giáo dục.
15 Nguyễn Bá Kim (2009), Phương pháp dạy học môn Toán, Nxb Đại học sư
phạm.
16 Nguyễn Bá Kim, Đinh Nho Chương, Nguyễn Mạnh Cảng, Vǜ Dương Thụy, Nguyễn Văn Thường (1994), Phương pháp dạy học môn Toán (Phần 2) – Dạy học những nội dung cụ thể, Nhà xuất bản Giáo dục.
17 Đào Thái Lai, Nguyễn Danh Nam (2011), Mô hình Toulmin trong lập luận và chứng minh hình học, Kỷ yếu Hội thảo quốc gia về giáo dục toán học ở trường phổ thông, Nxb Giáo dục Việt Nam.
18 Nguyễn Lân (2006), Từ điển từ và ngữ Việt Nam, NXB Tổng hợp TPHCM.
sư phạm.
19 Nguyễn Danh Nam, Phát triển chương trình môn toán phổ thông, Tạp chí
khoa học Giáo dục.
20 Nguyễn Danh Nam (2013), Sử dụng suy luận ngoại suy trong quá trình
chứng minh hình học,Tạp chí Giáo dục, số 319, Tr.41-43.
21 Nguyễn Danh Nam, Vǜ Thị Ngận, Năng lực suy luận thống kê của HS trung học phổ thông, Tạp chí Giáo dục, số đặc biệt tháng 5, Tr.162-165.
22 Vǜ Thị Ngận, Phát triển năng lực suy luận thống kê cho HS lớp 10 ở trường trung học phổ thông, Luận văn thạc sĩ Giáo dục.
23 Nguyễn Thị Ni (2015), Sử dụng mô hình Toulmin để phân tích quá trình lập luận và chứng minh của HS, Luận văn thạc sĩ Giáo dục.
24 Nguyễn Đăng Minh Phúc (2013), Tích hợp các mô hình thao tác động với môi trường dạy học toán điện tử nhằm nâng cao khả năng khám phá kiến thức mới của HS, Luận án tiến sĩ khoa học Giáo dục.
25 Trương Thị Khánh Phương (2015), Sử dụng biểu diễn trực quan hỗ trợ suy luận quy nạp và ngoại suy của HS mười năm tuổi trong quá trình tìm kiếm quy luật toán, Luận án Tiến sĩ khoa học Giáo dục, Trường ĐHSP Tp Hồ Chí Minh.
26 Đỗ Đức Thái (chủ biên), Đỗ Tiến Đạt, Lê Tuấn Anh, Đỗ Đức Bình, Phạm Xuân Chung, Nguyễn Sơn Hà, Phạm Sỹ Nam, Vǜ Phương Thúy, Dạy học phát triển năng lực môn Toán trung học cơ sở, Nhà xuất bản Đại học Sư phạm, 2018.
27 Nguyễn Quang Uẩn, Trần Hữu Luyến, Trần Quốc Thành (2013), Tâm lí học đại cương, NXB ĐHQG Hà Nội.
28 Trần Trung, Đặng Xuân Cương, Nguyễn Văn Hồng, Nguyễn Danh Nam, Ứng dụng công nghệ thông tin vào dạy học môn toán ở trường trung học phổ thông, Nxb Giáo dục Việt Nam.
29 Trần Vui, Biểu diễn trực quan trong việc học toán, Tạp chí Giáo dục, số
227, Tr.53-55.
30 Xavier Roegiers (1996), Khoa sư phạm tích hợp hay làm thế nào để phát
triển các năng lực ở nhà trường, NXB Giáo dục.
B. Tiếng Anh
31 Arcavi, A. (2003), The role of visual representations in the learning of
mathematics”, Educational Studies in Mathematics, Vol. 52, pp. 215-241.
32 Asli S, Ozgun-Koca (1998), Students’ use of representation in mathematics education, International Group for the Psychology of Mathematics Education, USA.
33 Boero, P. Douek, N. Morselli, F. & Pedemonte, B. (2010), Argumentation and proof : a contribution to theoretical perspectives and their classroom implementation. In Printo, M. M. F. & Kawasaki, T. F. (Eds.). Proceedings of the 34th Conference of the International Group for the Psychology of Mathematics Education, Vol. 1, pp. 179-209. Belo Horizonte, Brazil: PME
34 Boero, P., Garuti, R., Mariotti M. A. (1996). Some dynamic mental processes underlying producing and provingconjectures. In L. Puig & A. Gutierrez (Eds.), Proceedings of the Twentieth
35 Eco, U. (1983), Horns, hooves, insteps: some hypotheses on three types of abduction, In U. Eco