Biện Pháp 3 : Làm Cho Học Sinh Biết Phát Hiện Những Bước Thay Đổi Từ Sự

Do S, A1, A'1 thẳng hàng nên: OS

xOA1 (1 - x)OA1

OS 

x a 3 (1 - x)b

Có thể bạn quan tâm!

Phát triển tư duy biện chứng của học sinh trong dạy học Hình học ở trường trung học phổ thông - 16
Phát triển tư duy biện chứng của học sinh trong dạy học Hình học ở trường trung học phổ thông - 17
Phát triển tư duy biện chứng của học sinh trong dạy học Hình học ở trường trung học phổ thông - 18
Biện Pháp 4 : Làm Cho Học Sinh Có Khả Năng Xem Xét Các Đối Tượng Toán Học Trong Sự Mâu Thuẫn Và Thống Nhất
Biện Pháp 6 : Làm Cho Học Sinh Thấy Được Mối Liên Hệ Giữa Các Kiến Thức Toán Học Với Thực Tiễn
Sự Lựa Chọn Và Phối Hợp Các Biện Pháp

Xem toàn bộ 225 trang tài liệu này.

(1). Do S, A2, A'2 thẳng hàng nên:

6 8

OS 

yOA

(1 - y)OA OS y a 3 (1 - y)b

(2)

21 2 2 4

Do hai vectơ a, b không cùng phương nên từ (1), (2) ta có:

xy

6 2



x - 3





8 (1 - x) 3 (1 - y)

y - 1

3 4

OS 

- 3OA1

 4OA'1 OS

- 1

OA 3

3 OA'

Do 13

= 1 nên S, A3, A'3 thẳng hàng. Suy ra A1A'1, A2A'2, A3A'3 đồng quy tại S.

2 2

* PP thứ hai: Chọn một điểm thích hợp làm gốc vectơ. Biểu diễn các vectơ có gốc chung và các điểm ngọn lần lượt thuộc các đường thẳng đã cho theo cùng hệ vectơ chọn trước. Tiếp đó chứng tỏ rằng, tìm được các điểm thích hợp để các vectơ được xét là bằng nhau, từ đó suy ra các điểm ngọn của các vectơ này trùng nhau, nghĩa là các đường thẳng đã cho đồng quy tại điểm ngọn chung của các vectơ ấy. Cơ sở của PP này là dựa trên BT sau đây:

BT gốc: Các đường thẳng a1, a2, ... , ak đồng quy khi và chỉ khi tồn tại các điểm M1, M2, ... , Mk tương ứng thuộc các đường thẳng a1, a2, ... , ak sao cho với O tùy ý thì

OM1 = OM 2 = ... = OM k .

Giải: - Điều kiện cần: Nếu các đường thẳng a1, a2, ... , ak đồng quy tại M thì M thuộc tất cả các đường thẳng này, nên có thể chọn các điểm M1, M2, ... , Mk cùng trùng với điểm M, tương ứng thuộc a1, a2, ... , ak. Khi đó:

OM1 = OM 2 = ... = OM k = OM

- Điều kiện đủ: Nếu

OM1 =

OM 2 = ... =

OM k = OM thì các điểm M1, M2, ... , Mk

trùng nhau và trùng với M, nghĩa là các đường thẳng a1, a2, ... , ak đồng quy tại M. Dó đó từ BT tổng quát trên, ta có thể giải hàng loạt BT sau:

BT 1: Cho tam giác ABC. Qua mỗi đỉnh của tam giác vẽ đường thẳng song song

với đường thẳng đi qua M và trung điểm của cạnh đối diện.

CMR: các đường thẳng vẽ bằng cách như vậy đồng quy. N

Giải: Kí hiệu D, E, F lần lượt là trung điểm các cạnh BC, CA, AB của tam giác ABC. AN1, BN2, CN3 là các đường thẳng tương ứng song

song với các đường thẳng MD, ME, MF. B C

AN1 // MD 

AN1 k1 MD

MN1 - MA

k1 MD

Hình 2.49

MN 1

MA 1 k

1 (MB MC)

(1)

BN2 // ME 

CN3 // MF 

MN 2

MN 3

MB 1 k

MC 1 k

2 (MA MC)

3 (MA MB)

(2)

(3)

Chọn k1 = k2 = k3 = 2. Từ (1), (2), (3) ta có:

MN 1 MN 2 MN 3 MN MA MB MC

Suy ra: N1  N2  N3  N

Vậy các đường thẳng AN1, BN2, CN3 đồng quy tại N.

BT 2: Cho tam giác ABC và điểm M tùy ý. Các điểm M1, M2, M3 tương ứng là các điểm đối xứng của M đối với các trung điểm C1, A1, B1 của các cạnh AB, BC, CA. CMR: các đường thẳng CM1, AM2, BM3 đồng quy.

Hướng dẫn: Gọi N1, N2, N3 trung điểm của CM1, AM2, BM3

Ta chứng minh: MN 1 MN 2 MN 3

Suy ra các đường thẳng CM1, AM2, BM3 có trung điểm chung.

BT 3: Cho bốn điểm A, B, C, D và điểm M tùy ý. Qua trung điểm của mỗi đoạn thẳng có các mút là hai điểm trong bốn điểm đã cho, vẽ đường thẳng tương ứng song song với đường thẳng đi qua điểm M là trung điểm đoạn thẳng nối hai điểm còn lại. Chứng minh rằng, các đường thẳng vẽ bằng cách như vậy đồng quy tại một điểm.

BT 4: Cho hai hình bình hành ABCD và A1B1C1D1 sắp xếp sao cho B1 thuộc cạnh AB, D1 thuộc cạnh AD. Chứng minh rằng các đường thẳng DB1, BD1, CC1 đồng quy.

BT 5: Cho bốn điểm A, B, C, D và điểm M tùy ý. Qua mỗi điểm A, B, C, D vẽ đường thẳng song song với đường thẳng đi qua M và trọng tâm tam giác xác định bởi ba điểm còn lại.

Chứng minh rằng các đường thẳng vẽ được bằng cách như vậy đồng quy tại một điểm N.

Như vậy, trong quá trình DH theo hướng phát triển TDBC cho HS, GV cần dựa trên quan điểm: TD quan trọng hơn kiến thức, nắm vững PP quan trọng hơn thuộc lí thuyết.

Trên cơ sở so sánh các trường hợp riêng lẻ, dùng phép tương tự để chuyển từ trường hợp riêng này sang trường hợp riêng khác, khai thác mối liên hệ mật thiết với trừu tượng hoá, làm rõ mối quan hệ chung riêng giữa mệnh đề xuất phát và mệnh đề tìm được bằng đặc biệt hoá và hệ thống hoá, tạo khả năng tìm được nhiều giải pháp trên nhiều góc độ và tình huống khác nhau, khả năng tìm ra những mối liên hệ trong những sự kiện bên ngoài tưởng chừng như như không có liên hệ với nhau, khả năng tìm giải pháp là duy nhất. Các HĐ này góp phần rèn luyện tính nhuần nhuyễn cũng như tính nhạy cảm vấn đề của TD.

VD 2: Xét các BT.

BT 1: Cho tứ diện vuông OABC (vuông tại O). Chứng minh rằng hình chiếu của

đỉnh O lên mặt phẳng (ABC) là trực tâm tam giác AB

Giải: Gọi H là hình chiếu của O lên mp(ABC).

Vì OA  (OBC) OA  BC.

Theo định lí ba đường vuông

Hình 2.50

góc suy ra AH  BC.

Tương tự BH  CA, CH  AB. Vậy H là trực tâm tam giác ABC.

BT 2: Chứng minh rằng: Trong một tứ diện đều, hình chiếu của một đỉnh lên mặt đối diện là trực tâm tam giác của mặt đó.

Giải: Giả sử ABCD là tứ diện đều, A1 là hình chiếu của A lên mặt (BCD). Gọi B2 là trung điểm của CD. Suy ra AB2  CD (tam giác ACD đều)

 CD  (ABB2)  (ABB2)  ( (BCD). A

Vì AA1  (BCD) suy ra AA1  (ABB2)

 B, A1, B2 thẳng hàng và BA1 là đường B

cao của (BCD).

Tương tự ta có CA1

và DA1

cũng là các

C A1 D

đường cao của (BCD.

Vậy A1 là trực tâm tam giác BCD.

Hình 2.51

Nhận xét của GV qua hai BT trên: Dễ thấy OA  BC (BT 1); AB  CD (BT 2). Tức là hai tứ diện trên thuộc vào loại tứ diện có các cặp cạnh đối vuông góc.

Yêu cầu HS phát biểu BT tổng quát: CMR trong tứ diện trực tâm thì một đường cao của tứ diện đi qua trực tâm của mặt đáy tương ứng.

Lời giải tương tự với hai BT trên.

VD 3: Các mệnh đề xuất phát để dẫn đến "Định lí hàm số sin trong KG". BT 1: Cho góc tam diện vuông Ox, Oy, Oz. CMR:

SinxOy 

Sin(Oz)

SinyOz 

Sin(Ox)

SinzOx Sin(Oy)

(Kí hiệu (Ox), (Oy), (Oz) là độ lớn các góc nhị diện cạnh Ox, Oy, Oz)

Giải: BT là hiển nhiên. Vì xOy = (Oz) = 900.

BT 2: Cho hình chóp tam giác đều S.ABC. CMR:

SinASC Sin(SC)

SinBSC 

Sin(SA)

SinCSA Sin(SB)

Giải: Hiển nhiên. Vì ASB = BSC = CSA và (SA) = (SB) = (SC).

BT 3: Cho tứ diện trực tâm ABCD

CMR:

SinBAC Sin( AD)

SinCAD 

Sin( AB)

SinDAB Sin( AC)

Giải: Giả sử BB1  (ACD) thì B1 là trực tâm tam giác ACD  CB1  AD, DB1

 AC. Gọi B2 = DB1x AC; B3 = CB1 x AD. Khi đó: BB2  AC; BB3  AD. Do đó: (AC) = BB 2B1; (AD) = BB 3B1.

A Ta có: BB1 = BB2.sinBB 2B1

(tam giác BB 2B1 vuông tại B1)

= BB3.sinBB

3B1

C (tam giác BB 3B1 vuông tại B1)

Hình 2.52 Mà BB2 = AB.sinBAC (tam giác BAB2 vuông tại B2) BB3 = AB.sinBAD (tam giác BAB3 vuông tại B3)

Suy ra: SinBAC.sin(AC) = SinBAD.sin(AD)

SinBAC SinCDAB

(1)

Sin( AD) Sin( AC)

Tương tự, ta cũng có:

SinBAC SinCAD

(2)

Sin( AD) Sin( AB)

Từ (1) và (2) suy ra điều phải chứng minh.

Từ cách khai thác các trường hợp đặc biệt trên, GV có thể hướng dẫn, gợi ý HS phát biểu BT tổng quát sau (Định lí hàm số sin trong KG):

Cho góc tam diện Ox, Oy, Oz.

Ba góc phẳng ở đỉnh là , ,  ( =yOz,  = z x,  = xOy).

Chứng minh rằng:

SinSinSin

Sin(Ox) Sin(Oy) Sin(Oz)

Trong quá trình DH, GV phải cung cấp cho HS những tri thức về PP để HS tự tìm tòi, tự phát hiện và phát biểu vấn đề, dự đoán được các kết quả, tìm được hướng giải của một BT, hướng chứng minh của một định lí.

Chẳng hạn, PP suy luận quy nạp hoàn toàn: Đó là suy luận đi từ cái riêng đến cái chung.

Quy nạp hoàn toàn rút ra kết luận nói rằng tính chất A thuộc về tất cả các phần tử của tập hợp đang xét, trên cơ sở biết rằng tính chất A thuộc về mọi phần tử tập hợp đó.

Sơ đồ: A(x1)  ( A(x2)  ...  ( A(xn)  A(x). Trong đó x lấy các giá trị từ 1 đến n.

VD 4: Các BT xuất phát:

BT1: Cho hình nón đỉnh S đáy là hình tròn tâm (O, R), thiết diện qua trục hình nón là một tam giác đều. Gọi (S1) là mặt cầu nội tiếp hình nón có tâm O1, bán kính r1; V1, V lần lượt là thể tích của hình cầu (S1) và hình nón.

Chứng minh rằng:

V 1  1

V 2

BT 2: Cho hình nón đỉnh S đáy là hình tròn (O, R). Thiết diện qua trục hình nón là một tam giác đều. Gọi (S1) là mặt cầu nội tiếp hình nón có tâm O1, bán kính r1; (S2) là mặt cầu tiếp xúc với (S1) và mặt xung quanh của hình nón có tâm là O2, bán kính r2; V1, V2, V lần lượt là thể tích của các hình cầu (S1), (S2) và hình nón.

Chứng minh:

V1 V2  1

V 2

Từ đó ta có BT tổng quát: Cho hình nón đỉnh S đáy là hình tròn tâm O, bán kính

R. Thiết diện qua trục của hình nón là một tam giác đều, (S1 là mặt cầu nội tiếp hình nón có tâm O1 bán kính r1; (S2) là mặt cầu tâm O2 bán kính r2 tiếp xúc với (S1) và mặt xung quanh của hình nón; (S3) là mặt cầu tâm O3 bán kính r3 tiếp xúc với (S2) và mặt xung quanh của hình nón, ... , (Sn) là mặt cầu tâm On, bán kính rn tiếp xúc với mặt cầu (Sn-1) và mặt xung quanh của hình nón.

Chứng minh rằng: n  N, tổng thể tích của (S1), (S2), (S3), ..., (Sn) luôn nhỏ hơn nửa thể tích của hình nón.

2.5.3. Biện pháp 3: Làm cho học sinh biết phát hiện những bước thay đổi từ sự biến đổi về lượng sang biến đổi về chất

- TDBC giúp HS thấy được mối quan hệ "lượng" và "chất" của sự vật. Từ đó, HS có thể cảm nhận quy luật "lượng - chất" của lôgic BC.

- Khi DH toán cần giúp HS thấy được những bước chuyển hoá của đối tượng toán học.

VD 1: Xét ba điểm A, B, C có: AC = a; AB = b; BC = c như Hình 2.53

A.b B c C.

Hình 2.53

Khi đó, nếu ta có: b + c = a thì A, B, C thẳng hàng.

Hay ta có thể viết b1 + c1 = a1 thì A, B, C thẳng hàng.

Nếu ta nâng số mũ lên bậc hai: b2 + c2 = a2 thì A, B, C không thẳng hàng nữa mà

tạo thành một tam giác ABC vuông tại A. B

Như vậy, khi ta nâng lũy thừa lên, tức là

có sự thay đổi về lượng thì vị trí của A, B, c

C không còn giữ nguyên như trước nữa mà

A, B, C chuyển từ ba điểm thẳng hàng thành ba đỉnh của một tam giác vuông, tức là có sự thay đổi về chất.

Nếu ta tiếp tục nâng lũy thừa lên bậc n 3,

A C

Hình 2.54

ta có bn + cn = an thì tam giác ABC từ vuông trở thành nhọn. Thật vậy, từ biểu thức bn + cn = an thì suy ra a là cạnh lớn nhất.

Do đó, để chứng minh ABC nhọn, ta chỉ cần chứng minh góc A nhọn. Từ giả thiết đã cho, ta có:

an = bn + cn = b2.bn2 + c2.cn2 < b2.an2 + c2.an2 = an2(b2 + c2)

2 2 2

Suy ra, a2 < b2 + c2.

Áp dụng định lí côsin trong tam giác, ta có:

cos A

b c a  0 2bc

Vậy A là góc nhọn, do đó B, C cũng là góc nhọn hay tam giác ABC nhọn.

Nhận xét: Khi ta nâng lũy thừa từ 2 lên n 3, tức là tạo ra sự biến đổi về lượng thì tam giác ABC từ tam giác vuông chuyển sang tam giác nhọn, tức là có sự thay đổi về chất.

VD 2: Biện luận vị trí tương đối của 2 đường thẳng sau theo tham số m.

1: 4x my + 4 m = 0

2: (2m + 6)x + y 2m 1 = 0 [15, tr. 100].

Giải

Ta có:

D 4

2m  6

m = 2(m2 + 3m + 2) = 2(m + 1)(m + 2)

m Dx 1

4 m

 2m  1

= 2(m2 + m 2) = 2(m 1)(m + 2)

D  4 m

y  2m  1

2m  6

= 2(m2 5m 14) = 2(m 7)(m + 2)

- Khi: D 0 m 1 và m 2 thì 1 cắt 2 tại 1 điểm

x



M: 

Dx

m  1

m  1

m  7

Khi: D = 0 m 1





m 2



y

I D

m  1

* Với m = 1 thì Dx =  4 0 1 // 2.

* Với m = 2 thì Dx = 0; Dy = 0 hay D = Dx = Dy = 0 1 2

Nhận xét: Khi giá trị của D; Dx; Dy thay đổi (có sự biến đổi về lượng) thì vị trí cuả 2 đường thẳng 1 và 2 có thể cắt nhau tại 1 điểm M, hoặc là song song hoặc là trùng nhau (tức có sự thay đổi về chất).

VD 3: Trong mặt phẳng tọa độ Oxy, cho một phương trình có dạng:

x y

a 2 b 2

 1 (*) (a, b >0)

Xác định hình dạng đồ thị của phương trình trên.

Giải:

- Nếu a = b thì phương trình (*) là một đường tròn tâm O(0 ; 0), bán kính R = a = b.

- Nếu a b thì phương trình (*) là có đồ thị là một Elip.

+ a > b > 0: Elip có trục lớn là 0x, trục bé 0y.

+ b > a > 0: Elip có trục lớn là 0y, trục bé 0x.

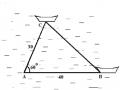
VD 4: Cho Conic (C) có: M( 1; 2m), tiêu điểm F(m; 2m), m 0.

: x  5 = 0 là đường chuẩn.