Biện Pháp 6 : Làm Cho Học Sinh Thấy Được Mối Liên Hệ Giữa Các Kiến Thức

* Cho M(1; 2),

M ' 9 ;12 . Viết đường thẳng d là đường trung trực của đoạn MM’. Trả





Có thể bạn quan tâm!

Phát triển tư duy biện chứng của học sinh trong dạy học Hình học ở trường trung học phổ thông - 18
Biện Pháp 3 : Làm Cho Học Sinh Biết Phát Hiện Những Bước Thay Đổi Từ Sự Biến Đổi Về Lượng Sang Biến Đổi Về Chất
Biện Pháp 4 : Làm Cho Học Sinh Có Khả Năng Xem Xét Các Đối Tượng Toán Học Trong Sự Mâu Thuẫn Và Thống Nhất
Sự Lựa Chọn Và Phối Hợp Các Biện Pháp
Phát triển tư duy biện chứng của học sinh trong dạy học Hình học ở trường trung học phổ thông - 23
Phát triển tư duy biện chứng của học sinh trong dạy học Hình học ở trường trung học phổ thông - 24

Xem toàn bộ 225 trang tài liệu này.

lời được các câu hỏi này sẽ làm cho HS nhìn nhận Toán học một cách toàn diện hơn và thấy được bản chất của nó.

BT 2: Phương trình của đường tròn (C) tâm I (x0; y0), bán kính R là:

2 2 2

x x0 y y R (1) thì ta cũng có:

0 o 0 0

x 2 y 2  2x x  2 y y x 2 y 2 R 2  0

a x0

b

Đặt y

2 2 2

c x0 y0 R

Ta được:

x 2 y 2  2ax  2by c  0

(2) cũng là phương trình đường tròn.

Nhưng BT “ngược”: Mỗi phương trình có dạng (2) với a, b, c tùy ý có phải đều là phương trình của 1 đường tròn hay không?

Câu trả lời là không. Phương trình (2) chỉ là đường tròn khi: a 2 b 2 c  0 .

2.5.6. Biện pháp 6: Làm cho học sinh thấy được mối liên hệ giữa các kiến thức Toán học với thực tiễn

- TDBC ở đây là:

+ Làm rõ mối liên hệ BC: "Từ trực quan sinh động đến TD trừu tượng, từ TD trừu tượng đến thực tiễn" với tư cách là quy luật của lôgic BC mà Lênin đã vạch ra.

+ Thực tiễn là chân lí "kiến thức Toán học".

- Trong DH Toán thực tiễn có hai phạm vi:

+ Trong Toán học: Vận dụng lí thuyết để giải toán thuần túy về toán.

+ Trong thực tế: Giải các BT thực tế, minh hoạ hay chứng minh các kiến thức toán là tồn tại.

Qua đó: HS học toán tốt hơn; HS biết vận dụng điều đã học vào thực tiễn xã hội.

Phần từ: Từ trực quan sinh động  TD trừu tượng ở các phần trên đã trình bày. Thực tiễn là tiêu chuẩn chân lí (kiến thức Toán). Ở đây bổ sung thêm cho hoàn chỉnh bước thứ hai từ: TD trừu tượng  thực tiễn.

Vận dụng kiến thức này để giải các BT trong thực tế.

VD 1: Dùng HH sơ cấp tại thực địa

Với những mục đích thực tế, thường xuất hiện sự cần thiết phải tiến hành việc dựng hình tại chỗ, chẳng hạn khi xây nhà, khi mở đường hoặc khi đo đạc các công trình tại chỗ. Trước hết trong mục này ta giả thiết những công việc trên được tiến hành trên mặt đất bằng phẳng. Có thể nghĩ rằng, như vậy các công việc này chẳng khác gì về bản chất với công việc dùng compa và thước để vẽ các đường tròn, các cung và các đường thẳng bất kì, còn tại thực địa khi khoảng cách giữa các điểm khá lớn muốn làm điều đó ta lại phải dùng những sợi dây dài hoặc những cái thước khổng lồ, mà không phải lúc nào cũng có. Mà nói chung vẽ trực tiếp lên đất mọi cung hoặc mọi đường thẳng là công việc rắc rối. Ở đây để hiểu các BT ta đưa ra các hạn chế:

- Không tiến hành kẻ các đường thẳng thực trên mặt đất, mà chỉ đánh dấu chúng. Chẳng hạn, bằng các dãy cọc dày đặc tạo ra các điểm. Đối với nhu cầu thực tế điều này không thiếu.

- Cấm vẽ trên đất các cung nói chung, dù nhỏ hay lớn. Vì vậy trên thực tế ta không có compa. Một tác dụng nữa của compa là đặt trên các đường thẳng những khoảng cụ thể, thì chúng ta giả thiết các đoạn này không cho bằng số mà nhờ vào hai điểm tại chỗ ở đâu đó đã được đánh dấu bằng các chiếc cọc. Bởi bản thân các khoảng cách sẽ được đo bằng các bước chân, các bàn chân, các ngón tay hoặc mọi vật phù hợp với việc này.

Với hai hạn chế trên, thêm vào đó lại không sử dụng thước đo độ công việc dĩ nhiên là khó khăn, chính vì lẽ đó ta có các BT cụ thể sau:

BT 1: Đánh dấu đường thẳng

Tại chỗ ta dùng cọc đánh dấu hai điểm cách xa nhau. Làm thế nào để đánh dấu đường thẳng đi qua chúng, và làm như thế nào để không cần có người giúp đỡ vẫn có thể đóng được cọc trên đường thẳng giữa hai điểm đó?

Cách làm: Đầu tiên dùng mắt ngắm sao cho cọc thứ ba che khuất hai cọc A và B, vị trí cọc thứ ba này nằm trên đường thẳng chung AB kéo dài về phiá đầu A, hoặc phía đầu B, như vậy ta không khó khăn gì có thể xác lập vị trí C của chiếc cọc thứ ba

nằm trên đường thẳng AB kéo dài. Sau đó các điểm của đoạn AB kéo dài có thể dựng được nhờ cách làm vừa rồi, bởi vì, các điểm này sẽ nằm hoặc trên AC kéo dài, hoặc trên BC kéo dài (tuỳ thuộc vào điểm A hay điểm B nằm gần điểm C hơn). Nói chung, điểm bất kì của đường thẳng AB sẽ nằm trên đường kéo dài của một trong các đoạn thẳng AB, AC, hoặc BC.

BT 2: Giao điểm giữa các đường thẳng

Bằng các cọc đánh dấu hai điểm của một đường thẳng và hai điểm của đường thẳng thứ hai. Làm thế nào để tìm giao điểm của hai đường thẳng này?

Cách làm: Cũng dùng mắt ngắm như BT 1, dễ dàng có thể tìm được giao điểm, bởi vì nó nằm trên cả hai đường thẳng kéo dài cả hai đoạn thẳng với các đầu được đánh dấu tại các điểm đã cho.

BT 3: Đối xứng qua một điểm

Tại thực địa ta đánh dấu hai điểm A, B.

Hãy tìm điểm C đối xứng với điểm A qua B?

Cách làm: Tiếp tục kéo dài AB từ điểm B và đặt trên nó điểm C cùng độ dài AB từ điểm B. Để làm điều này cần phải đo bằng một đơn vị nào đó

thích hợp khoảng cách giữa các điểm A và B (chẳng hạn: Như bước chân, gang tay, hộp diêm, ...)

VD 2: Hai chiếc tàu thủy cùng xuất phát từ một vị trí A, đi thẳng theo hai hướng tạo với nhau góc 600. Tàu B chạy với tốc độ 20 hải lí một giờ. Tàu C chạy với tốc độ 15 hải lí một giờ. Sau 2 giờ, hai tàu cách nhau bao nhiêu hải lí? (1 hải lí 1,852 km) [126, tr. 54].

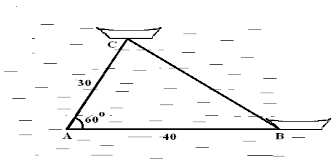
Giải: Sau 2 giờ, tàu B đi được 40 hải lí, tàu C đi được 30 hải lí.

Hình 2.59

Từ BT thực tế trên, ta có BT HH:

Cho tam giác ABC có AB = 40, AC = 30, Aˆ= 600. Tính BC?

Áp dụng định lí côsin vào tam giác ABC, ta có: a2 = b2 + c2 2bc.cosA

BC2 = AC2 + AB2  2.AC.AB.cos A

= 302 + 402  2. 30.40.cos 600

= 900 + 1600  1200 = 1300

1300

Vậy BC = 36 (hải lí)

Sau 2 giờ, hai tàu cách nhau khoảng 36 hải lí.

Đây là một BT xuất phát từ thực tế, có thể dùng để minh họa cho HS khi học về định lí côsin trong tam giác, để từ đó giúp HS thấy được rằng: Toán học bắt nguồn từ thực tiễn rồi trở về phục vụ thực tiễn.

VD 3: BT thực tế: Cho hai lực F 1

1200

100N

F 1

và F 2 có cùng điểm đặt tại O. F 1 và F 2

đều có cường độ là 100 N, góc hợp bởi F 1

100N

và F

2 bằng 1200.

Hình 2.60

F 2

Tìm cường độ lực tổng hợp của hai lực ấy [126, tr. 15].

Giải: Theo quy tắc hình bình hành, ta dựng

hình bình hành nhận OF1, OF2 làm các cạnh. O

100N

F 1 A

Khi đó, ta có lực tổng hợp cần tìm là:

F = F 1 + F 2 = OB

Áp dụng định lí côsin trong tam giác.

Ta có: OB2 = OA2 + AB2 2.OA.AB.cos 600

= 1002 + 1002 2.100.100. 1 = 1002

100N 1200

F 2 F

C Hình 2.61 B

OB = 100.

Vậy cường độ lực tổng hợp là: F =

= 100 N.

VD 4: Trên nóc một tòa nhà có một cột ăng-ten cao 5m. Từ vị trí quan sát A cao 7m so với mặt đất, có thể nhìn thấy đỉnh B và chân C của cột ăng-ten dưới góc 500 và 400 so với phương nằm ngang.

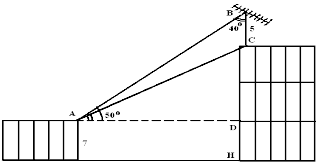
Tính chiều cao của tòa nhà [126, tr. 67].

Hình 2.62

Giải: Từ BT thực tế, ta có BT HH: Theo Hình 2.62, ta có:

BC = 5m, AI = 7m,

BAD = 500,

CAD= 400. Tính CH.

Tam giác ABC có: BAC

= 500 400 = 100,

ABC = 900 500 = 400.

Theo định lí sin trong tam giác ABC, ta có: B

sin100

AC

sin 400

AC  5.sin 40 5m

18.5 (m)

400

40050

sin100 C

Trong tam giác vuông ACD.

Ta có: sin 400 = CD

A D

CD = AC.sin 400

= 18,5.sin 400 11,9 (m)

Chiều cao của tòa nhà là:I

CH = CD + DH 11,9 + 7 18,9 (m)

Hình 2.63

BT trên là một BT thực tế, được áp dụng khi HS học bài “Hệ thức lượng trong tam giác”, cụ thể là khi học về định lí sin trong tam giác.

VD 5: Một đường hầm xuyên qua núi có chiều rộng là 20m, mặt cắt đứng của đường hầm có dạng nửa elip như hình vẽ.

Biết rằng tâm sai của đường elip là e  0,5 .

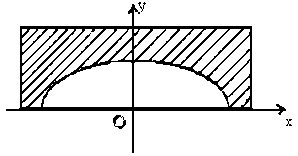
Hãy tìm chiều cao của đường hầm đó [126, tr. 101]. Giải: Gọi chiều cao của đường hầm là: b (b > 0).

Hình 2.64

Nửa trục lớn của elip là:

a  10m.

Elip có nửa tiêu cự là:

c a.e  5m

a 2 c 2

Chiều cao của đường hầm là: b 

 8,7m

100  25

Đây là một BT thực tế, được áp dụng khi HS học xong bài “Đường elip”.

VD 6: Vệ tinh nhân tạo đầu tiên được Liên Xô (cũ) phóng từ Trái Đất năm 1957. Quỹ đạo của vệ tinh đó là một đường elip nhận tâm của Trái Đất là một tiêu điểm. Người ta đo được vệ tinh cách bề mặt Trái Đất gần nhất là 583 dặm và xa nhất là 1342 dặm (1 dặm 1,609 km).

Tìm tâm sai của quỹ đạo đó biết bán kính của Trái Đất xấp xỉ 4000 dặm [126, tr. 103].

Giải:

. .

A’

Gọi tâm Trái Đất là F2 và giả sử quỹ đạo

chuyển động của vệ tinh có phương trình:

A1 A2

x y

a 2 b2

 1.

Hình 2.65

Khi đó khoảng cách từ vệ tinh đến tâm

Trái Đất là:

d a c x .

Do a x a

nên

a c d a c .

Gọi R là bán kính Trái Đất thì

a c  583 R



a c  1342 R

2a  1925  2R

2c  759



Tâm sai của quỹ đạo là: e 

759

1925  2R

 759

1925  8000

 0,07647 .

2.5.7. Biện pháp 7: Làm cho học sinh biết chú trọng các thao tác tư duy

a. Kết hợp PP phân tích và PP tổng hợp

- TDBC ở đây là xem xét sự vật một cách tổng thể, cảm nhận được quy luật “toàn diện” của Lôgic BC.

Tìm được các mối liên hệ giữa các mặt của các sự vật có liên quan.

- Khi giải các BT làm cho HS thấy được mối liên hệ giữa các yếu tố bằng các PP: PP tổng hợp, PP phân tích.

+ PP tổng hợp: Đi từ cái đã biết đến cái chưa biết. PP này được trình bày rất nhiều trong SGK.

+ PP phân tích: Đi từ cái chưa biết đến cái đã biết. Bao gồm phân tích đi lên và phân tích đi xuống.

Việc kết hợp hai PP này giúp HS nhìn nhận một BT, một định lí, ... một cách

tường tận hơn. A

VD 1: Chứng minh rằng: Trong tam giác ABC

Ta có:

a 

sin A

sin B

c

sin C

[126, tr. 56].

1 2 b

Giải: Trước hết ta chứng minh:

sin B

c

sin C

(1).

H a C

Thực vậy: Kẻ AH BC

AH .AC AB 0

AH .AC AH .AB

AH .BC  0

Hình 2.66

AH .AC.cos Aˆ2AH .AB.cos Aˆ

b.cos Aˆ2c.cos Aˆ

b.sin C c.sin B

( sin C  cos Aˆ2, sin B  cos Aˆ1, phụ chéo)

b

sin B

c

sin C

(1) được chứng minh.

*Chứng minh: Làm tương tự.

sin A

b

sin B

(2).

Từ (1) và (2) suy ra BT được chứng minh.

Ta có sơ đồ chứng minh trên theo PP tổng hợp:

A0 A1 A2  .... An 1 An X (định lí, BT)

1444442444443

Mệnh đề, giả thiết đã biết. Cụ thể:

Bài này bước A0 là: kẻ AH BC, ... , bước A7 = X là:

sin B

c

sin C

(đpcm).

Chú ý: - Nếu gọi A là mệnh đề cần chứng minh và Ai (i = 1, ... , n) hoặc là tiên đề, định lí, định nghĩa, giả thiết thì sơ đồ của phép tổng hợp là:

A1A2  ...An1AnX. Nói cách khác đi là từ A1 suy ra A2, từ A2 suy ra A3, và cho đến An1 suy ra An = X.

- Phép tổng hợp thường dùng để trình bày cách chứng minh.

VD 2: Cho 3 điểm A(3; 0), B(5; 4) và P(10; 2). Viết phương trình đường thẳng

đi qua P đồng thời cách đều A và B [126, tr. 90].

Hướng dẫn: Định hướng phân tích P(10 ; 2)



Phương của 

A,B ở cùng phía của :

d A; d B;  // AB

VTCP của  là AB .

A B

A,B ở về hai phía của :



d A; d B; 

 đi qua trung điểm K của AB VTCP của  là PK .

.

Sơ đồ 2.2

ٱ Kٱ