Thiết Kế Và Xây Dựng Phần Mềm Thực Nghiệm

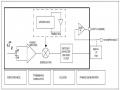
hướng, góc liệng của TBB trong không gian phục vụ cho quá trình ĐKĐH cho TBB.

4.3 Thiết kế và xây dựng phần mềm thực nghiệm

Với mục đích tổng hợp bộ lọc số, việc đầu tiên cần phải thực hiện đó là rời rạc hóa mô hình trạng thái (3.9) ở chương 3. Rời rạc hóa hệ phương trình đó có thể sử dụng các phương pháp xấp xỉ khác nhau, ở đây ta sẽ sử dụng xấp xỉ Euler. Còn việc xấp xỉ hệ phương trình (3.10) có thể thực hiện bằng giải tích. Với việc sử dụng các phương pháp đã nêu ta thu được mô hình rời rạc của bộ lọc như sau



H1x (k  1)  H1x (k)  T*1y(k)H1z (k) 1z (k)H1y(k)



H1y (k  1)  H1y (k)  T* 1x (k)H1z (k) 1z (k)H1x (k)



H1z (k  1)  H1z (k)  T*1z (k)H1y(k) 1y(k)H1x (k)

Có thể bạn quan tâm!

• Mô Phỏng Đánh Giá Các Mô Hình Hệ Thống Xác Định Vtg Đã Xây Dựng
• Nghiên cứu xác định định hướng không gian của thiết bị bay theo các phép đo từ trường trái đất - 13
• Thiết Kế Và Tổ Chức Phần Cứng Thực Nghiệm
• Cấu Trúc Các Kênh Điều Khiển Định Hướng Tbb Và Phương Pháp Phối Ghép Với Các Bộ Đo Góc Và Vtg
• Nghiên cứu xác định định hướng không gian của thiết bị bay theo các phép đo từ trường trái đất - 17
• Nghiên cứu xác định định hướng không gian của thiết bị bay theo các phép đo từ trường trái đất - 18

Xem toàn bộ 151 trang tài liệu này.

 (k  1)  (1 T ) (k)  w (k)

1x



T1x

1x x

 (k  1)  (1 

T )

(k)  w (k)

1y



T1y

1y y

 (k  1)  (1  T )

(k)  w (k)

1z



T1z

1z z

(4.1)

Để đơn giản cho sử dụng ta sẽ viết hệ phương trình (4.1) dưới dạng ma trận – vector như sau:

Ở đây:

x(k 1)  fk (x(k),tk )  w(k)

(4.2)

x(k) H1x (k)

H1y (k)

H1z (k)

H1x (k)

1x (k)

1y (k)

1z (k)T

(4.3)

là vector trạng thái.

Để tổng hợp được thuật toán lọc ta cần phải lựa chọn các phép đo sao cho hệ thống là có thể quan sát được. Như đã đề cập ở các chương 2 và 3 thì việc chỉ sử dụng riêng các cảm biến từ trường theo ba trục không thể quan sát

được đơn trị các trạng thái của hệ thống, do đó ta cần phải sử dụng thêm ít nhất một cảm biến VTG bổ sung. Phương án tốt nhất đã đề cập, ta sẽ sử dụng một cảm biến VTG có trục nhạy trùng với trục OY1 của hệ TĐLK.

Như vậy vector quan sát đối với bộ lọc cần tổng hợp gồm có các phép đo

từ trường ba trục theo hệ TĐLK và một phép đo VTG thẳng đứng, vector đo được biểu diễn như sau

T

z(k) H (k) H (k) H (k)  (k) v(k)

(4.4)

1x 1y 1z 1y 

Ở đây v(k) là vector nhiễu đo, được giả thiết là tạp trắng Gauss có mật độ phổ đã biết.

Như vậy nhiệm vụ của bài toán lọc là ở chỗ, dựa vào các quan sát (phép đo) ở (4.4) bằng cách tốt nhất ta sẽ ước lượng vector trạng thái x(k) ở (4.3) mà động học của các trạng thái này được mô tả bởi hệ phương trình (4.1).

Điểm mới mà ta có được khi sử dụng mô hình toán học đã nêu đó là việc ta sẽ ước lượng chính các thành phần VTT theo ba trục. Hơn nữa, lựa chọn mô hình này sẽ làm đơn giản đi rất nhiều việc thực hiện thuật toán lọc, vì tính các phép đo là hàm tuyến tính của các trạng thái cần ước lượng. Sau đây ta sẽ lần lượt xem xét phương pháp xây dựng các bộ lọc phi tuyến tối ưu, dưới dạng chương trình phần mềm, theo những thuật toán đã giới thiệu ở mục 3.2 của chương 3.

4.3.1 Phần mềm thuật toán Extended Kalman Filter (EKF)

1. Algorit chương trình

Lọc Kalman mở rộng EKF dùng để ước lượng các trạng thái/tham số của hệ thống phi tuyến ngẫu nhiên. Tính phi tuyến thể hiện có thể hoặc ở mô hình động học trạng thái, hoặc ở mô hình đo, hoặc có thể ở cả hai mô hình. Tính ngẫu nhiên thể hiện ở sự bất định về mô hình động học và sai số của phép đo.

Đối với bài toán lọc đã nêu thì tính phi tuyến xuất hiện chỉ ở phương trình trạng thái, mô hình quan sát là tuyến tính. Hàm vector mô tả động học trạng thái f được xác định từ (4.2), ma trận độ nhạy phép đo H được xác định từ phương trình đo (4.4), các ma trận phương sai nhiễu quá trình Qk và ma trận phương sai nhiễu đo Rklà đã biết. Do đó có thể thực hiện thuật toán lọc Kalman mở rộng theo lưu đồ thuật toán ở hình 4.12

Khởi tạo bộ lọc

xˆ0 Ex0



P

x0

 E (x  xˆ )(x  xˆ )T 



0 0 0 0



Tính hệ số khuếch đại lọc

K  P ()HT[HP ()HT  R ]1

k k

k

k

Cập nhật phép đo

xˆk()  xˆk()  Kk(zk Hxˆk())

Tính ma trận phương sai hậu nghiệm

Pk ()  [I  KkH]Pk ()

Tăng bước vòng lặp

k  k 1

Thuật toán dự báo một bước

xˆk1()  f (xˆk())

A

k1 x xxˆ k()

f |

P ()  A P ()AT  Q

k1

k1 k k1 k

Vector đo theo thời gian z1, z2,…

Vector ước lượng tối ưu xˆ k

Hình 4.12 Lưu đồ thuật toán lọc EKF

2. Giao diện khởi tạo, hiển thị

Chương trình thực nghiệm sử dụng kết hợp hai ngôn ngữ lập trình Labview và Matlab để đảm bảo sự thuận tiện theo giao diện chương trình, cũng như khả năng thực hiện các phép toán phức tạp. Để thực hiện thuật toán lọc EKF phần mềm sẽ được tổ chức như sau:

Thứ nhất, phần mềm đảm bảo lấy mẫu các dữ liệu phép đo. Phần này được thực hiện nhờ các subVIs có trong thư viện của Labview. Các phép đo sẽ được lấy mẫu đồng thời, được đưa vào bộ đệm, sau đó đọc từ bộ đệm và đưa vào VI chính để cập nhật phép đo.

Thứ hai, phần mềm đảm bảo thực thi thuật toán. Phần này được thực hiện nhờ VI chính. Được viết trên ngôn ngữ Matlab. Phần này gồm có:

- Phần khởi tạo chương trình, nhằm mục đích khởi tạo các tham số ban đầu, đặt các hằng số;

- Phần thực hiện thuật toán theo lưu đồ hình (4.12).

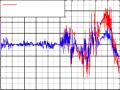
Cuối cùng là phần mềm đảm bảo giao diện hiển thị kết quả. Để so sánh thì trên mỗi đồ thị đều

hiển thị các giá trị

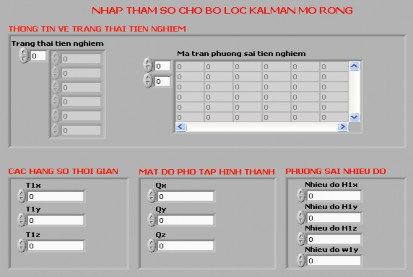
Hình 4.13 Giao diện nhập tham số bộ lọc EKF

thực và giá trị sau lọc của mỗi trạng thái. Giao diện thể hiện phần nhập tham số cho bộ lọc được thể hiện ở hình (4.13).

4.3.2 Phần mềm thuật toán Unscented Kalman Filter (UKF)

Thuật toán lọc EKF trong thực tế chỉ có thể áp dụng cho các hệ thống gần như tuyến tính, đối với các hệ thống có tính phi tuyến cao thì việc áp dụng thuật toán này trở nên không hiệu quả. Về bản chất, thuật toán lọc EKF

được dựa trên việc tuyến tính hóa các hàm phi tuyến, điều này gây ra sai số rất lớn đối với các hệ thống phi tuyến nếu như ở một thời điểm nào đó trong hệ thống xuất hiện các điểm gián đoạn mà ở đó ma trận Jacobi không tồn tại hoặc hệ thống ở một trạng thái nào đó mà ma trận Jacobi bị suy biến. Để khắc phục hạn chế này, phép biến đổi Unscented (UT) đã được phát triển như là một phương pháp truyền thông tin kỳ vọng và phương sai qua các phép biến đổi phi tuyến. Phương pháp này chính xác hơn, dễ thực hiện hơn, và quan trọng là khối lượng tính toán tương đương với tuyến tính hóa.

Cũng giống như thuật toán lọc EKF, việc thực hiện thuật toán lọc Kalman Unscented (UKF) cũng được tiến hành từng bước, lặp lại các phương trình của thuật toán. Hàm f mô tả động học hệ thống và hàm độ nhạy đo VTT tương ứng được xác định từ các hệ phương trình (4.1) và (4.4). Ma trận phương sai nhiễu quá trình Qk và nhiễu đo Rk đã biết.

Các trọng số được xác định dựa trên phép biến đổi Unscented theo các

công thức sau

wm 

0 L 



wc  (1 2 )

(4.5)



0 L 

wm  wc 1

i  1, 2,...2L

Ở đây:

i i



2(L )

+ L là kích thước của vectơ trạng thái (L=6);

+ xác định độ trải phổ (spread) của các điểm sigma (104  1);

+  (2  1)L , là hằng số với mục đích hợp nhất phần thông tin tiên niệm

của phân bố và đã chứng minh được là đối với phân bố Gauss thì  2

1. Algorit chương trình

là tối ưu.

Khởi tạo bộ lọc

xˆ0 Ex0

P  E

(x  xˆ )(x  xˆ )



Tính các điểm sigma

k1 xˆk1, xˆk1 

(1)Px, xˆk1  (1)Px

x0





T

0 0 0 0





k1

k 1 

Các phương trình cập nhật thời gian

*  f ( )



k|k1 k1

w 



2n





ˆ m *

k|k1 i i,k|k1

i0





2n

P  wm (*

ˆ

)(*

ˆ

)T  Q

xk|k 1



i0

i i,k|k1 k|k1 i,k|k1 k|k1 k1

ˆ ,ˆ (1 )P ,ˆ

 (1 )P 

k|k1 k|k1 k|k1 xk|k 1

k|k1 xk|k 1 

 H



k|k1 k|k1

2n

Zˆ wm

k|k1





i0

i i,k|k1

Vector đo theo thời gian

z1, z2, …

Các phương trình cập nhật phép đo





2n

P  wc( Zˆ

)( Zˆ

)T  R

xk xk



i0

i i,k|k1 k|k1 i,k|k1 k|k1 k

P

2n



 wc(ˆ

)(ˆ

)T  R

xk zk



i0

i i,k|k1 k|k1 i,k|k1 k|k1 k

K  P P1

k xk zk

xˆ  xˆ

xk xk

 K (z

 Zˆ

), P  P

 K P KT

k k|k1 k k k|k1 xkxk|k 1 k xkxkk

Vector trạng thái ước lượng tối ưu xˆ k

Hình 4.14 Lưu đồ thuật toán lọc UKF

2. Giao diện khởi tạo, hiển thị

Tổ chức chương trình thực hiện thuật toán lọc UKF cơ bản cũng giống như đối với thuật toán EKF. Điểm khác biệt là ở chỗ:

Ở phần thứ nhất của bước thứ hai, ngoài việc khởi tạo các tham số, đặt các giá trị hằng, còn có thêm phần tính toán các trọng số của phép biến đổi Unscented;

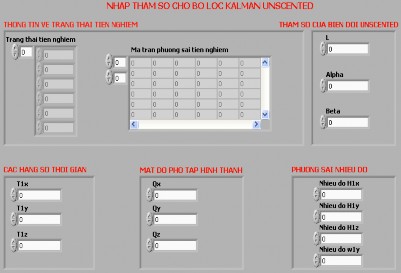
Ở phần thứ hai của bước thứ hai, để thuận tiện cho việc tính toán ta xây dựng các chương trình con để tính toán việc truyền kỳ vọng và phương sai của hàm phi tuyến dựa trên phép biến đổi Unscented. Việc nhập tham số cho bộ lọc được thực hiện thông qua giao diện hình (4.15).

Hình 4.15 Giao diện nhập tham số cho lọc UKF

4.3.3 Phần mềm thuật toán lọc Kalman thích nghi (MS-AUKF)

Kết quả đo của các cảm biến từ trường chịu ảnh hưởng đáng kể của sai số thăng giáng ngẫu nhiên. Sai số này thay đổi phụ thuộc vào điều kiện bay, tác động của từ trường các hệ thống điện trên khoang thiết bị bay. Để đảm bảo độ chính xác ước lượng ta cần sử dụng thuật toán lọc thích nghi theo phương sai của nhiễu đo.

Như mục 3.2.3. của chương 3 đã nêu, bộ lọc MS-AUKF được đề xuất trên cơ sở hình thành bởi hai UKF song song. Tại mỗi bước thời gian, UKF- master ước lượng “Trạng thái/Tham số” từ phương sai nhiễu thu được bởi UKF-slaver, trong khi UKF-slaver ước lượng phương sai nhiễu sử dụng Innovations được tạo bởi UKF-master.

1. Algorit của thuật toán lọc MS-AUKF

Tổ chức chương trình lọc Kalman Unscented thích nghi về cơ bản cũng giống như tổ chức phần mềm để thực hiện thuật toán lọc UKF. Khác biệt ở chỗ ta cần xây dựng thêm một bộ lọc Kalman tiêu chuẩn (tham chiếu) để ước lượng phương sai nhiễu đo. Phần mềm bảo đảm bảo giao diện vì vậy cũng được bổ sung để đánh giá khả năng thích nghi của thuật toán (xem hình 4.16).

2. Giải pháp phần mềm nâng cao chất lượng của bộ lọc

T

Như đã đề cập ở các chương 2 và 3, để có thể ước lượng một cách chính xác các thành phần VTG không được quan sát, thì yêu cầu đặt ra đối với cảm biến VTG bổ sung là phải có độ chính xác cao. Tuy nhiên ta vẫn có thể sử dụng một cảm biến vận tốc góc có độ chính xác không cao để làm cảm biến bổ sung. Điều này có thể thực hiện được nếu như loại trừ được sai số đo VTG của cảm biến này. Trong mục 4.2 đã lựa chọn cảm biến LY510ALH dạng MEMS làm cảm biến bổ sung. Bằng cách ước lượng sai số bias của cảm biến này ta có thể bù được ảnh hưởng của nó đến độ chính xác ước lượng, nâng cao chất lượng của bộ lọc. Như vậy sai số bias của LY510ALH sẽ được bổ sung vào vector trạng thái. Khi đó vector trạng thái là

x (k) H (k) H (k) H (k)

 (k)

 (k)

 (k) x (k)

(4.6)

new

1x 1y 1z 1x 1y 1z bias 

ở đây xbias(k) là bias của cảm biến VTG.

Ma trận độ nhạy phép đo H sẽ thay đổi vì phép đo tốc độ góc lúc này sẽ là

1ydo (k) 1y (k)  xbias (k)  v1y (k)

(4.7)

Bias của MEMs được mô tả bởi quá trình ngẫu nhiên dạng random-walk

xbias (t)  wth/bias (t)

với wth/bias (t) là tạp trắng Gauss có mật độ phổ đã biết.

Hay dưới dạng rời rạc hóa

xbias (k 1)  xbias (k)  Twth/bias (k)

(4.8)

(4.9)

Xem tất cả 151 trang.