CÂU HỎI CHƯƠNG 1
1. Trình bày mục tiêu của TTNT.
2. Trình bày khái niệm cơ bản về TTNT.
3. Nêu các tiền đề cơ bản của TTNT.
4. Nêu các kỹ thuật trong TTNT.
5. Nêu vai trò của TTNT trong công nghệ thông tin.
6. Nêu các thành phần của TTNT.
7. Nêu những lĩnh vực nghiên cứu và ứng dụng cơ bản của TTNT.
8. Nêu những vấn đề đang được giải quyết của TTNT.
CHƯƠNG 2: CÁC CHIẾN LƯỢC TÌM KIẾM
2.1. Biểu diễn vấn đề trong không gian trạng thái
Bài toán tìm kiếm, một cách tổng quát, có thể hiểu là tìm một đối tượng thỏa mãn một số yêu cầu trong một tập hợp các đối tượng. Có rất nhiều vấn đề mà việc giải quyết nó được quy về bài toán tìm kiếm, do đó cần phải xác định không gian tìm kiếm. Không gian tìm kiếm bao gồm tất cả các đối tượng mà ta cần quan tâm tìm kiếm. Nó có thể là không gian liên tục, chẳng hạn không gian các véctơ thực n chiều; nó cũng có thể là không gian các đối tượng rời rạc.
Trong mục này ta sẽ xét việc biểu diễn một vấn đề trong không gian trạng thái sao cho việc giải quyết vấn đề được quy về việc tìm kiếm trong không gian trạng thái.
2.1.1. Không gian trạng thái của bài toán
Muốn biểu diễn một vấn đề trong không gian trạng thái, cần xác định các yếu tố sau:
(1) Trạng thái ban đầu;
(2) Một tập hợp các toán tử, trong đó mỗi toán tử R mô tả một hành động hoặc một phép biến đổi có thể đưa một trạng thái u tới một trạng thái v.
Tập hợp tất cả các trạng thái có thể đạt tới từ trạng thái ban đầu bằng cách áp dụng một dãy toán tử, lập thành không gian trạng thái của vấn đề.
Ta sẽ ký hiệu không gian trạng thái là U, trạng thái ban đầu là uo (uoU). Mỗi toán tử R có thể xem như một ánh xạ R: UU.
Một tập hợp T các trạng thái kết thúc (trạng thái đích) TU.
Khi biểu diễn một vấn đề thông qua các trạng thái và các toán tử thì việc tìm nghiệm của bài toán được quy về việc tìm đường đi từ trạng thái ban đầu tới trạng thái đích. (Một đường đi trong không gian trạng thái là một dãy toán tử dẫn một trạng thái tới một trạng thái khác).
Do đó, không gian trạng thái có thể biểu diễn bằng đồ thị định hướng, trong đó mỗi đỉnh của đồ thị tương ứng với một trạng thái. Nếu có toán tử R biến đổi trạng thái u thành trạng thái v, thì có cung gán nhãn R đi từ đỉnh u tới đỉnh v (trạng thái v được gọi là kề với trạng thái u). Khi đó một đường đi trong không gian trạng thái sẽ là một đường đi trong đồ thị này.
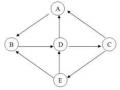
Ví dụ 2.1: Xét không gian trạng thái có uo=A, T={B} và được miêu tả bằng đồ thị sau:
A
G
C
E
D
F
B
Hình 2.1. Mô tả không gian trạng thái bằng đồ thị định hướng
Trong đồ thị Hình 2.1, ta có:
- uo =A
- T={B}
- Tập các toán tử:
Tên toán tử | Ý nghĩa | |
1 | R1 | AG |
2 | R2 | AE |
3 | R3 | CA |
4 | R4 | CF |
5 | R5 | EG |
6 | R6 | EC |
7 | R7 | GD |
8 | R8 | DE |
9 | R9 | DB |
10 | R10 | FB |
11 | R11 | BE |
Có thể bạn quan tâm!
-
Nhập môn trí tuệ nhân tạo - 1 -
Nhập môn trí tuệ nhân tạo - 2 -
Hiểu Và Mô Hình Hoá Ngữ Nghĩa Ngôn Ngữ Tự Nhiên -
Các Chiến Lược Tìm Kiếm Kinh Nghiệm (Tìm Kiếm Heuristic) -
Đồ Thị Không Gian Trạng Thái Ví Dụ 2.13 -
Đồ Thị Và Hoặc Biểu Diễn Toán Tử A B, C, D
Xem toàn bộ 272 trang tài liệu này.
2.1.2. Các ví dụ
Sau đây là các ví dụ về các không gian trạng thái được xây dựng cho một số vấn đề.
Ví dụ 2.2: Trò chơi 8 số
Trong bảng ô vuông 3 hàng, 3 cột, mỗi ô chứa một số nằm trong phạm vi từ 1 đến 8 sao cho không có 2 ô có cùng giá trị, có một ô trong bảng bị trống (không chứa giá trị nào). Xuất phát từ một sắp xếp nào đó các số trong bảng, hãy dịch chuyển ô trống sang
1 | 2 | 3 |
4 | 5 | |
6 | 7 | 8 |
1 | 2 | 3 |
4 | 5 | 6 |
7 | 8 |
phải, sang trái, lên trên hoặc xuống dưới sao cho ô trống không ra ngoài bảng để đưa bảng A về bảng B (Hình 2.2).
Bảng A Bảng B
Hình 2.2. Trò chơi 8 số
Trong bài toán này, trạng thái ban đầu là Bảng A, còn trạng thái kết thúc là Bảng B. Tương ứng với các quy tắc chuyển dịch các quân, ta có bốn toán tử: up (đẩy quân lên trên), down (đẩy quân xuống dưới), left (đẩy quân sang trái), right (đẩy quân sang phải). Chẳng hạn, từ trạng thái ban đầu (bảng A), ta chỉ có thể áp dụng các toán tử down, left, up.
2 | 3 | |
4 | 5 | |
6 | 7 | 8 |
down
left
up
2 | 3 | |
1 | 4 | 5 |
6 | 7 | 8 |
1 | 2 | 3 |
4 | 5 | |
6 | 7 | 8 |
1 | 2 | 3 |
6 | 4 | 5 |
7 | 8 |
Trong Ví dụ 2.2. việc tìm ra một biểu diễn thích hợp để mô tả các trạng thái của vấn đề là khá dễ dàng và tự nhiên. Song trong nhiều vấn đề việc tìm được biểu diễn thích hợp cho các trạng thái của vấn đề là hoàn toàn không đơn giản. Việc tìm ra dạng biểu diễn tốt cho các trạng thái đóng vai trò hết sức quan trọng trong quá trình giải quyết một vấn đề. Có thể nói rằng, nếu ta tìm được dạng biểu diễn tốt cho các trạng thái của vấn đề, thì vấn đề hầu như đã được giải quyết.
Ví dụ 2.3: Nhà buôn và kẻ cướp
Có ba nhà nhà buôn và ba kẻ cướp cùng một chiếc thuyền chở được một hoặc hai người ở bên bờ tả ngạn một con sông. Hãy tìm cách để chở 3 kẻ cướp và 3 nhà buôn đi thuyền từ tả ngạn sang hữu ngạn sông sao cho ở mỗi bờ sông, số nhà buôn ở mọi thời điểm luôn không nhỏ hơn số kẻ cướp (trừ trường hợp bên một bờ sông không có nhà buôn nào). Nhà buôn và kẻ cướp có thể qua lại hai bên bờ sông nhiều lần.
Để biểu diễn các trạng thái, ta sử dụng bộ ba (a, b, k), trong đó a là số nhà buôn, b là số kẻ cướp ở bên bờ tả ngạn, k = 1 nếu thuyền ở bờ tả ngạn và k = 0 nếu thuyền ở bờ
hữu ngạn. Như vậy, không gian trạng thái cho bài toán nhà buôn và kẻ cướp được xác định như sau:
- Trạng thái ban đầu là (3, 3, 1).
- Các toán tử: Có năm toán tử tương ứng với hành động thuyền chở qua sông 1 nhà buôn, hoặc 1 kẻ cướp, hoặc 2 nhà buôn, hoặc 2 kẻ cướp, hoặc 1 nhà buôn và 1 kẻ cướp (do thuyền chỉ chở được tối đa 2 người).
- Trạng thái kết thúc là (0, 0, 0).
- Một lời giải cho bài toán như sau:
Trạng thái | Giải thích | |
1 | (3, 3, 1) | Bắt đầu |
2 | (3, 1, 0) | Chở 2 kẻ cướp sang sông từ tả ngạn sang hữu ngạn |
3 | (3, 2, 1) | Chở 1 kẻ cướp sang sông từ hữu ngạn sang tả ngạn |
4 | (3, 0, 0) | Chở 2 kẻ cướp sang sông từ tả ngạn sang hữu ngạn |
5 | (3, 1, 1) | Chở 1 kẻ cướp sang sông từ hữu ngạn sang tả ngạn |
6 | (1, 1, 0) | Chở 2 nhà buôn sang sông từ tả ngạn sang hữu ngạn |
7 | (2, 2, 1) | Chở 1 kẻ cướp, 1 nhà buôn sang sông từ hữu ngạn sang tả ngạn |
8 | (0, 2, 0) | Chở 2 nhà buôn sang sông từ tả ngạn sang hữu ngạn |
9 | (0, 3, 1) | Chở 1 kẻ cướp sang sông từ hữu ngạn sang tả ngạn |
10 | (0, 1, 0) | Chở 2 kẻ cướp sang sông từ tả ngạn sang hữu ngạn |
11 | (0, 2, 1) | Chở 1 kẻ cướp sang sông từ hữu ngạn sang tả ngạn |
12 | (0, 0, 0) | Chở 2 kẻ cướp sang sông từ tả ngạn sang hữu ngạn |
Ví dụ 2.4:
Cho 2 bình A và B lần lượt có dung tích 3 lít và 5 lít và không có vạch chia độ. Ban đầu 2 bình không có nước. Có thể rót nước đổ đầy các bình, có thể đổ hết nước từ một bình đi, có thể rót nước từ bình này sang bình khác.
Hãy xây dựng không gian trạng thái của bài toán để rót được đúng 4 lít nước trong bình B và hãy chỉ ra 1 cách rót.
Sử dụng bộ (a, b) để biểu diễn mỗi trạng thái, trong đó a là lượng nước của bình A, b là lượng nước của bình B tại thời điểm đang xét.
- Trạng thái ban đầu là (0, 0);
- Tập trạng thái kết thúc là T={(x, 4), 0≤x≤3}
- Các toán tử:
STT | Toán tử | Giải thích |
1 | (a, b) (0, b) (a>0) | Đổ hết nước ở bình A |
2 | (a, b) (a, 0) (b>0) | Đổ hết nước ở bình B |
3 | (a, b) (3, b) (a<3) | Đổ đầy nước ở bình A |
4 | (a, b) (a, 5) (b<10) | Đổ đầy nước ở bình B |
5 | (a, b) (a+b, 0) (a+b3) | Đổ hết nước ở bình B sang bình A |
6 | (a, b) (0, a+b) (a+b5) | Đổ hết nước ở bình A sang bình B |
7 | (a, b) (3, a+b-3) (a<3, a+b>3) | Đổ một phần nước từ bình B sang bình A sao cho bình A đầy nước |
8 | (a, b) (a+b-5, 5) (b<5, a+b>5) | Đổ một phần nước từ bình A sang bình B sao cho bình B đầy nước |
Không gian trạng thái có thể biểu diễn dạng đồ thị như sau:
Hình 2.3. Đồ thị biểu diễn cách rót nước
- Tìm một cách rót:
Trạng thái | Giải thích | |
1 | (0, 0) | Trạng thái ban đầu |
2 | (0, 5) | Đổ đầy nước vào bình B |
STT | Trạng thái | Giải thích |
3 | (3, 2) | Đổ 3 lít nước từ bình B sang bình A |
4 | (0, 2) | Đổ hết nước từ bình A |
5 | (2, 0) | Đổ 2 lít nước từ bình B sang bình A |
6 | (2, 5) | Đổ đầy nước bình B |
7 | (3, 4) | Đổ 1 lít nước từ bình B sang bình A |
Như vậy, một cách rót là:
(0,0) (3,0) (0,3) (3,3) (1,5) (1,0) (0,1) (0,1) (3,1) (0,4).
Ngoài ra, còn một cách rót khác như sau:
(0, 0) (0, 5) (3, 2) (0, 2) (2, 0) (2, 5) (3, 4).
Ví dụ 2.5. Bài toán tháp Hà Nội
Cho ba cọc 1, 2, 3. Ở cọc 1 ban đầu có 3 đĩa sắp xếp theo thứ tự to dần từ trên xuống dưới. Hãy dịch chuyển 3 đĩa đó sang cọc thứ 3 sao cho:
- Mỗi lần chỉ chuyển một đĩa;
- Trong mỗi cọc không cho phép đĩa to nằm trên đĩa nhỏ hơn.
Để biểu diễn các trạng thái, ta ký hiệu các đĩa là 1, 2, 3, trong đó đĩa 1 là lớn nhất và đĩa 3 là nhỏ nhất. Một trạng thái được biểu diễn bởi bộ (i, j, k) trong đó: đĩa 1 ở vị trí i, đĩa 2 ở vị trí j và đĩa 3 ở vị trí k.
Trạng thái đầu uo = (1, 1, 1);
Tập trạng thái kết thúc: T={(3, 3, 3)}
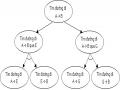
Không gian trạng thái của bài toán có thể miêu tả dạng đồ thị như sau:
Hình 2.4. Biểu diễn không gian trạng của bài toán Tháp Hà Nội.
Ví dụ 2.6. Trò chơi tic-tac-toe
Cho trước một bàn cờ n x n ô (n 3). Bắt đầu ván đấu bằng bàn cờ trống, đấu thủ thứ nhất có thể đặt ký hiệu"X"vào bất cứ ô nào trong n2 ô trống của bàn cờ, tiếp theo,
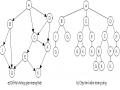
đấu thủ thứ hai đến lượt mình đi sẽ có thể đặt ký hiệu"0"của mình vào ô trống và sẽ cứ luân phiên như thế. Người nào đặt được k ô (3 k) thẳng hàng, cột hoặc đường chéo liền nhau là thắng (Hình 2.5).
Hình 2.5. Một phần không gian trạng thái của bài toán với n=3
2.2. Giới thiệu các chiến lược tìm kiếm
Có thể phân các chiến lược tìm kiếm thành hai loại:
2.2.1. Các chiến lược tìm kiếm mù
Trong các chiến lược tìm kiếm này, không có một sự hướng dẫn nào cho sự tìm kiếm, mà ta chỉ phát triển các trạng thái ban đầu cho tới khi gặp một trạng thái đích nào đó. Có hai kỹ thuật tìm kiếm mù, đó là tìm kiếm theo bề rộng và tìm kiếm theo chiều sâu.
Kỹ thuật tìm kiếm theo bề rộng là tìm kiếm trên tất cả các nút của một mức trong không gian bài toán trước khi chuyển sang các nút của mức tiếp theo. Tư tưởng của tìm kiếm theo bề rộng là các trạng thái được phát triển theo thứ tự mà chúng được sinh ra, tức là trạng thái nào được sinh ra trước sẽ được phát triển trước. Kỹ thuật tìm kiếm theo bề rộng bắt đầu từ mức thứ nhất của không gian bài toán, theo hướng dẫn của luật trọng tài, chẳng hạn"đi từ trái sang phải”. Nếu không thấy lời giải tại mức này, nó chuyển xuống mức sau để tiếp tục… đến khi tìm được lời giải (nếu có).
Kỹ thuật tìm kiếm sâu trong không gian bài toán được bắt đầu từ một nút rồi tiếp tục cho đến khi hoặc đến ngò cụt hoặc đến đích. Tại mỗi nút có luật trọng tài, chẳng hạn,"đi theo nút cực trái”, hướng dẫn việc tìm. Nếu không đi tiếp được, gọi là đến ngò cụt, hệ thống quay lại một mức trên đồ thị và tìm theo hướng khác, chẳng hạn, đến nút"sát nút cực trái”. Hành động này gọi là quay lui. Thuật toán tìm kiếm theo chiều