Mô Phỏng Đánh Giá Các Mô Hình Hệ Thống Xác Định Vtg Đã Xây Dựng

zˆ1,k  Hˆ1x,k ()



zˆ2,k  Hˆ1y,k ()



zˆ



zˆ

3,k  Hˆ1z,k 4,k ˆ1y,k

()

()

- Phương trình tính hệ số khuếch đại lọc:

k k k k k k k



1

K  P ()HTH P ()HT R 

1	0	0	0	0
0 	1	0	0	0
0	0	1	0	0

Có thể bạn quan tâm!

• Phương Sai Sai Số Tổng Khi Xác Định Các Thành Phần Của Vtg
• Thuật Toán Lọc Phi Tuyến Các Thành Phần Vector Vtg Của Tbb
• Các Thuật Toán Lọc Phi Tuyến Khác Trong Tổng Hợp Bộ Đo Vtg Của Tbb
• Nghiên cứu xác định định hướng không gian của thiết bị bay theo các phép đo từ trường trái đất - 13
• Thiết Kế Và Tổ Chức Phần Cứng Thực Nghiệm
• Thiết Kế Và Xây Dựng Phần Mềm Thực Nghiệm

Xem toàn bộ 151 trang tài liệu này.

0

0

Ở đây:

Hk 



0



0 0 0 0 1 0

- Phương trình tính ma trận phương sai tiên nghiệm:

k1 k k k k

P ()  A P ()AT  Q

1 Tˆ1z,k ()  Tˆ1y,k () 0  THˆ1z,k () THˆ1y,k () 



Tˆ1z,k () 1 Tˆ1x,k () THˆ1z,k () 0  THˆ1x,k () 



Tˆ

()

 Tˆ

() 1

 THˆ

() THˆ



() 0

Ở đây: A 

1y,k 1x,k 1y,k 1x,k 

k 0 0 0 (1 T / T ) 0 0 

1x 

0 0 0 0 (1 T / T ) 0 

1y 

0 0 0 0 0 (1 T / T1z ) 

- Phương trình tính ma trận phương sai hậu nghiệm:

Pk () I  Kk Hk Pk ()

3.4.2. Sử dụng thuật toán lọc Kalman Unscented Filter (UKF)

Thực tế sử dụng cho thấy thuật toán lọc Kalman mở rộng chỉ áp dụng tốt cho các hệ thống động học gần như tuyến tính, đối với các hệ thống có tính phi tuyến lớn thì chất lượng của thuật toán lọc Kalman mở rộng không đáp ứng được. Gần đây người ta sử dụng thuật toán lọc Kalman Unscented để ước lượng trạng thái và tham số của hệ động học có tính phi tuyến lớn. Thuật toán này có độ phức tạp tính toán cũng tương đương như thuật toán lọc Kalman mở rộng (EKF) nhưng độ chính xác cao hơn.

Phương trình mô tả hệ thống động học và phép đo cũng giống như các phương trình (3.9) và (3.10) của thuật toán EKF. Các phương trình thực hiện thuật toán lọc Kalman Unscented cụ thể như sau:

xˆ0 Ex0

+ Khởi tạo bộ lọc: P

 E(x

 xˆ )(x  xˆ

)T 

(3.18)

*

X0

0 0 0 0

Hàm:

Ex0 ,

PX0 được tính theo công thức (3.11) của thuật toán EKF.

(1)Pxk1

+ Dùng phép biến đổi Unscented để tính các điểm sigma:

k1 xˆk1, xˆk1 

(1)Px

k 1

, xˆk1 

(3.19)

Ở đây:

Px là ma trận phương sai sai số hậu nghiệm đã được mô tả ở

k1

phần thuật toán lọc Kalman rời rạc mở rộng.

+ Các phương trình cập nhật thời gian:

*

 fk 1(k 1)

k k 1

ˆ

2n m *

k k 1 



w x i i,k k 1 i 0

P 

2n

w m (*

ˆ

)(*

ˆ

)T  Q

xk k1

x i

i,k k 1

k k 1

i,k k 1

k k 1

k 1

i 0

(3.20)

k k 1 ˆk k 1,ˆk k 1 

(1 )Px

,ˆk k 1 

(1 )Px 





k k1

k k1 

k k 1  hk (k k 1)



Sˆ

2n

ˆ

w m S

k k 1

i 0

x i i,k k 1

+ Các phương trình cập nhật phép đo:

P 2n w c (

 Sˆ

)(

 Sˆ

)T  R

x k x k



x i

i 0

i, k k 1

k k 1

i,k k 1

k k 1 k

P

2n

 w c (

ˆ

)(

ˆ

)T  R

x k z k

x i

i 0

i, k k 1

k k 1

i, k k 1

k k 1

k (3.21)

K

 P



x z

k k k

xˆ  xˆ

1

P

x k z k

 K (S

 Sˆ

), P  P

 K P KT

k

i, k k 1

k k k k 1

x k k k 1

k x k x k k

Trong (3.20) và (3.21), Qk

và R k

tương ứng với ma trận phương sai của

nhiễu kênh trạng thái và nhiễu kênh đo, còn các trọng số có thể được tính theo phép biến đổi Unscented, tức là:

Wm 

0 L 



Wc 

 (1 2 )

(3.22)



0 L 

Wm  Wc 1

i  1,2,...2L

Với:

i

i 2(L )

+ L là kích thước của vectơ trạng thái;

+ xác định độ trải phổ (spread) của các điểm sigma (104  1);

+  (2 1)L ;

+ là một hằng số ứng với thông tin tiên nghiệm của phân bố , đối với

phân bố Gauss thì  2 là tối ưu.

Các phương trình sai phân mô tả quá trình và phương trình đo của kênh quan sát giống như được mô tả trong thuật toán lọc Kalman rời rạc mở rộng.

Vector trạng thái khởi tạo, ma trận phương sai sai số ban đầu, ma trận phương sai nhiễu đo, ma trận phương sai nhiễu quá trình và các hằng số thời gian của quá trình Markov cũng giống như thuật toán lọc Kalman rời rạc mở rộng.

Các phương trình sử dụng trong thuật toán cập nhật thời gian và cập nhật phép đo cũng được mô tả tương tự như ở trong thuật toán lọc Kalman rời rạc mở rộng.

3.4.3 Sử dụng kết hợp thuật toán lọc thích nghi và thuật toán lọc Kalman Unscented thích nghi (Master-Slaver Adaptive Unscented Kalman Filter (MS- AUKF)).

Khi sử dụng các cảm biến từ trường thì sai số thăng giáng ngẫu nhiên ảnh hưởng đáng kể tới kết quả đo. Sai số này thay đổi phụ thuộc vào điều kiện bay, tác động của từ trường của các hệ thống điện tử trên khoang TBB. Để đảm bảo độ chính xác ước lượng ta sử dụng thêm thuật toán lọc thích nghi khi tổng hợp bộ lọc UKF. Ta cần tổng hợp thuật toán lọc thích nghi theo phương sai của nhiễu đo. Có nhiều phương pháp lọc thích nghi, tuy nhiên với bài toán này chúng ta sẽ sử dụng thuật toán lọc Kalman Unscented thích nghi kiểu Master-Slaver Adaptive Unscented Kalman Filter.

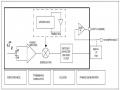
MS-AUKF được xây dựng trên cơ sở hai bộ lọc UKF song song (hình 3.4). Tại mỗi bước thời gian, UKF-master ước lượng “Trạng thái/Tham số” từ phương sai nhiễu thu được bởi UKF-slaver, trong khi UKF-slaver ước lượng phương sai nhiễu sử dụng những thay đổi (innovations) được tạo bởi UKF- master. Điều cần chú ý đó là hai UKF độc lập trong cấu trúc MS-AUKF. Bởi vậy UKF-slaver có thể được thay thế bởi một bộ lọc đơn giản hơn, ví dụ như

xˆk 1

UKF-Master

Cập nhật thời gian

xˆk|k 1

Cập nhật phép đo

xˆ

k

trạng thái

yk

vk innovation

ˆ

k 1

ˆ

k

phương sai nhiễu

UKF-Slaver

Cập nhật thời gian

ˆk|k 1

Cập nhật phép đo

Hình 3.4 Sơ đồ cấu trúc của bộ lọc MS-AUKF

bộ lọc Kalman để tiết kiệm thời gian tính toán trong ứng dụng thời gian thực. UKF-master hoạt động như một bộ lọc Kalman Unscented tiêu chuẩn. Vì vậy sau đây ta chỉ xem xét hoạt động của UKF-slaver.



k

Ta sử dụng i để ký hiệu cho phần tử đường chéo thứ i của ma trận

k

phương sai nhiễu đo Qv , nghĩa là:

Qv  diag(1 ,2 ,...m )

(3.23)

k k k k

Trong trường hợp động học của k

đã biết một cách rõ ràng, nghĩa là:

k  f (k1)  Wk

(3.24)

thì phương trình (3.24) có thể trực tiếp được sử dụng như là mô hình tham

chiếu của UKF-slaver. Trong khi không biết động học của sử dụng mô hình nhiễu tác động sau:

k k1  Wk

k , chúng ta có thể

(3.25)

với

wk được giả thiết là tạp trắng Gauss có kỳ vọng bằng không.

Phương sai của những thay đổi (innovation) tạo bởi UKF-master được

coi là tín hiệu quan sát đối với UKF-slaver, và theo các phương trình cập nhật phép đo, mô hình quan sát được mô tả như sau:

S  g(

)  diag 2n wc (

 y )(

 y )T  Qv 

(3.26)

k k i

i0

i,k k 1

k k 1

i,k k 1

k k 1

k 1



Phép đo của Sˆ

nhận được bởi UKF-slaver là: S

 diag(v vT )

với

vk  yk  yk|k1

k

là innovation và yk là phép đo thực.

k k k

Bởi vậy thuật toán đệ quy của UKF-slaver có thể được thực hiện như sau:

ˆ0 Ex0

+ Slave-I – Khởi tạo:





P0

 E(0

ˆ

0 )(0

ˆ

0 )T 

(3.27)

+ Slave-II – Tính các điểm sigma:

(1)Pk1,

(1)Pk 1

k1 ˆk1,ˆk1 

ˆk1 

(3.28)

+ Slave-III – Cập nhật thời gian:

*

 f(k 1)



ˆ

k k 1

2n

 wm *

k k 1

2n





i0

i i,k k 1

P  wm (*

ˆ

)(*

ˆ

)T  Q

i

k k 1





i0

i,k k 1

k k 1

i,k k 1

k k 1

(3.29)

(1 )P

k k 1

(1 )P

k k 1

k k 1 ˆk k 1,ˆk k 1  ,ˆk k 1 



 g ( )



k k 1 k k k 1

ˆ 2n m



i

Sk k 1 

wi,k k 1 i0

+ Slave IV – Cập nhật phép đo:



2n

P  wc (

 Sˆ

)(

 Sˆ

)T  R 



s k s k





i0 i

2n

i,k k 1 k k 1 i,k k 1 k k 1

P s

w c

(i,k k 1 ˆk k 1)(i,k k 1 ˆk k 1)T R 

(3.30)

k k



K  P

i0

i

P1

k



k s k

s k s k



k

ˆkˆi,k k 1  K

(Sk Sˆk k 1),

P k  Pk k 1  Kk P k k k

K



s

s

T

3.4 Mô phỏng đánh giá các mô hình hệ thống xác định VTG đã xây dựng

Điều kiện thực hiện mô phỏng đánh giá các mô hình ta vẫn làm như đối với mô hình thuật toán lọc phi tuyến với tín hiệu có sai số tiên nghiệm.

Để mô phỏng kiểm chứng các mô hình EKF, UKF và MS-AUKF, ta giả thiết rằng TBBKNL chuyển động tương đối VTT với các VTG không đổi

1x 1y 1z  0.1(rad / s) ; các góc ban đầu bằng 0; VTG của TBB

1y

đo nhờ

một cảm biến VTG độc lập bổ sung. Các hằng số thời gian của các quá trình Markov và mật độ phổ của nhiễu tạp tạo hình có thể xác định được thông qua các thông tin tiên nghiệm về sự thay đổi chậm của các thành phần vector vận tốc góc của thiết bị bay. Chính xác hơn thì hằng số thời gian và mật độ phổ nhiễu tạp tạo hình được xác định nhờ thực nghiệm bay của đối tượng.

Việc tổ chức mô phỏng thử nghiệm thống kê được thực hiện theo phương pháp Monte-carlo. Phương pháp này dựa trên việc sử dụng các giá trị có thể có của các đại lượng ngẫu nhiên với phân bố xác suất cho trước.

Khi dùng phương pháp thử nghiệm thống kê độ chính xác của đánh giá sẽ tăng nếu ta tăng số lượng thử nghiệm, khi tăng N đến một giới hạn nào đó độ chính xác của đánh giá hầu như không thay đổi dù N tiếp tục tăng.

Mối quan hệ giữa độ chính xác và số lượng thử nghiệm được đánh giá qua kỳ vọng và phương sai của các đại lượng ngẫu nhiên [12] được tính như sau:

m* ( t ) 

1N

yk ( t ),

D* ( t ) 

1N

[ yk ( t ) m* ( t )]2 , (3.31)

yi N k 1 i yi N k 1 i yi

Ở đây: N - số lần thử nghiệm;

i

y k ( t ) là giá trị thử nghiệm của

yi ( t ) trong lần thử nghiệm thứ k.

Các đánh giá

m* ( t ) và

D* ( t )là hàm ngẫu nhiên, việc chọn số N sao cho

yi

yi

chúng khác giá trị thực một đại lượng cho trước với xác suất cho trước

Theo quy trình các thuật toán lọc đã trình bày ở các mục 3.3.1 – 3.3.3, sử dụng phần mềm MatLaB để lập trình, ta nhận được những kết quả sau

							w*1x

1

Sai so

0.5

0

-0.5

-1

0 10 20 30 40 50 60 70 80 90 100

1

1

W1x

0.5

0

-0.5

-1

0 10 20 30 40 50 60 70 80 90 100

1

H1y

0

-1

0 10 20 30 40 50 60 70 80 90 100

							w*1z

1

Sai so

0.5

0

-0.5

-1

0 10 20 30 40 50 60 70 80 90 100

Thoi gian(s)

a) Khi không có nhiễu

phép đo VTT không có sai số

0

H1y

-1

0 10 20 30 40 50 60 70 80 90 100

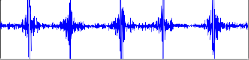
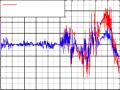
1

w1z

0.5

0

-0.5

-1

0 10 20 30 40 50 60 70 80 90 100

Thoi gian(s)

b) Khi có nhiễu phép đo VTT

có sai số lớn tại những điểm H1y=0

Hình 3.5 Kết quả khi tính trực tiếp vận tốc góc.

Khi cho nhiễu tác động nhỏ, sai số đánh giá các VTT và VTG sử dụng thuật toán EKF mô phỏng theo phương pháp thực nghiệm thống kê Monte Carlo được thể hiện trên hình 3.6

2

1.5

Sai so danh gia H1x

1

0.5

0

-0.5

-1

-1.5

-3

x 10

2

					Sai so danh gia H1x

1.5

Sai so danh gia w1x

1

0.5

0

-0.5

-1

-1.5

-3

x 10

-2

0 10 20 30 40 50 60 70 80 90 100

Thoi gian(s)

a. Sai số đánh giá H1x

-2

					Sai so danh gia w1x

0 10 20 30 40 50 60 70 80 90 100

Thoi gian(s)

d. Sai số đánh giá ω1x

2

1.5

Sai so danh gia H1y

1

0.5

0

-0.5

-1

-1.5

-2

-3

x 10

				Sai so danh gia H1y

0 10 20 30 40 50 60 70 80 90 100

Thoi gian(s)

b. Sai số đánh giá H1y

2

1.5

Sai so danh gia w1y

1

0.5

0

-0.5

-1

-1.5

-2

-3

x 10

				Sai so danh gia w1y

0 10 20 30 40 50 60 70 80 90 100

Thoi gian(s)

e. Sai số đánh giá ω1y

2

1.5

Sai so danh gia H1z

1

0.5

0

-0.5

-1

-1.5

-2

-3

x 10

				Sai so danh gia H1z

0 10 20 30 40 50 60 70 80 90 100

Thoi gian(s)

c. Sai số đánh giá H1z

2

1.5

Sai so danh gia w1z

1

0.5

0

-0.5

-1

-1.5

-2

-3

x 10

				Sai so danh gia w1z

0 10 20 30 40 50 60 70 80 90 100

Thoi gian(s)

f. Sai số đánh giá ω1z

Hình 3.6 Sai số đánh giá các VTT và VTG khi sử dụng thuật toán EKF. Mô phỏng theo phương pháp thực nghiệm Monte Carlo.