Nghiên cứu xác định định hướng không gian của thiết bị bay theo các phép đo từ trường trái đất - 17

y ,

z , E

- góc quay cánh lái tương ứng gật, hướng và liệng, [rad];

k0 , k1 - hệ số truyền mạch hồi tiếp theo góc và tốc độ góc quay cánh lái;

V2 2 2

q  - áp lực tốc độ, [N/ m ; kg/m.s ];

2

SM, SCL – tương ứng diện tích Miden và diện tích cánh lái, [m2]; L- chiều dài của TBB, [m];

Có thể bạn quan tâm!

• Thiết Kế Và Tổ Chức Phần Cứng Thực Nghiệm
• Thiết Kế Và Xây Dựng Phần Mềm Thực Nghiệm
• Cấu Trúc Các Kênh Điều Khiển Định Hướng Tbb Và Phương Pháp Phối Ghép Với Các Bộ Đo Góc Và Vtg
• Nghiên cứu xác định định hướng không gian của thiết bị bay theo các phép đo từ trường trái đất - 18

Xem toàn bộ 151 trang tài liệu này.

Xm, XF, XFlà các tọa độ tương ứng với trọng tâm, tâm áp lực thân và tâm áp lực cánh lái của TBB.

4.5.1 Hàm truyền các kênh điều khiển và ổn định TBB cánh phẳng

1. Biểu thức hàm truyền của TBB theo góc gật và góc tấn công

a. Hàm truyền TBB theo góc gật

K (p) 

(p) 

(a2a6  a3a4 )  a3p



y

(p)

p3  a p2  (a  a

4

1

2

)p  a1a4

(4.10)

K(p) 

KTBB (1  pTV )

2 2 

p 1  2TBBTTBBp  TTBBp

Chấp nhận một số phép đơn giản hóa, qua biến đổi có thể xác định được các tham số trong hàm truyền TBB theo góc gật như sau:

- Hệ số truyền của TBB: K

 a3.a4  a1.a6

(4.11)

- Hằng số thời gian TBB:

TBB

T 

a2  a1.a4

a2  a1.a4

1

(4.12)

- Hệ số tắt dần:

TBB

2 a2  a1.a4

TBB 

a1  a4

(4.13)

- Thời gian khí động:

Trong đó:

TV 

a3.a4

a3

 a2

.a6

(4.14)

q.S .L2

a  mz M ,[1/ s2] là hệ số cản khí động;

1 Z1

JZ1V

a2 

(C.q.S

 P).(XF

y

M

J

 Xm )

,[1/ s2 ] là hệ số ổn định tĩnh của TBB;

y

a3 

C.q.S

.(X J

Z1

CL

Fy

 Xm )

,[1/ s2 ] là hệ số hiệu quả cánh lái.

y

C.q.S

a M

Z1

 P

,[1/ s] gọi là hệ số động lực nâng do góc tấn công;

4 mV

C.q.S

a6 

y CL ,[1/ s] gọi là hệ số động lực nâng cánh lái.

mV

a  G.cos

7 mV

g ,[1/ s] do khi bay bằng, cos1.

V

b. Hàm truyền TBB theo góc tấn công

Từ phương trình hàm truyền TBB theo góc gật (4.10), sử dụng quan hệ động hình học giữa các góc, ta có thể rút ra hàm truyền TBB theo góc tấn công

K (p) (p) 

KTBB

(4.15)

(p)

1 2

TBB

2 2

p  T

p

TTBB TBB

2. Biểu thức hàm truyền TBB theo góc trượt và góc hướng

Để xác định biểu thức hàm truyền của TBB theo các góc trong mặt phẳng hướng, ta tiến hành biến đổi hệ phương trình lực – mômen và các phương trình động hình học về dạng Laplace tương tự như đã thực hiện cho mặt phẳng gật. Sử dụng những quan hệ lực, mômen, động hình học ta rút ra được các hàm truyền.

a. Hàm truyền theo góc hướng

K (p) (p) 

K'TBB (1 T'V p)

(4.16)

TBB

(p)

p(1 2'

TBB

T'TBB

p  T'2

p2 )

b. Hàm truyền theo góc trượt

K (p) (p) 

K'TBB

(4.17)

TBB

(p)

1 2'

TBB

T'TBB

p  T'2 p2

Do tính chất không đối xứng của sơ đồ khí động cánh phẳng của TBB các tham số trong các biểu thức (4.16) và (4.17) được xác định như sau

- Hệ số truyền của TBB: K'

 b3.b4  b1.b6

(4.18)

- Hằng số thời gian TBB:

TBB

T'TBB 

b2  b1.b4

b2  b1.b4

1

(4.19)

- Hệ số tắt dần:

'TBB 

b1  b4

(4.20)

2 b2  b1.b4

- Thời gian khí động:

T'V 

b3.b4

b3

 b2 .b6

(4.21)

Các hệ số động học

b1  b6

xác định một cách tương tự như cho mặt

phẳng gật nhưng với các tham số khí động và động lực riêng của mặt phẳng hướng với lưu ý là do cách bố trí cánh lái hướng, các hệ số cùng tên trong hai mặt phẳng có thể rất khác nhau về giá trị và dấu.

q.S .L2

b  mY M ,[1/ s2] là hệ số cản khí động;

1 Y1

JY1V

b2 

(C.q.S  P).(X  X )

z

M

F m

J

,[1/ s2 ]

là hệ số ổn định tĩnh của TBB;

Y1

C.q.S .(X  X )

b z CL FZ m,[1/ s2 ] là hệ số hiệu quả cánh lái.

3 J

Y1

C.q.S  P

b z M,[1/ s] hệ số động lực nâng do góc trượt;

4 mV



C.q.S

bz CL,[1/ s] hệ số động lực nâng cánh lái hướng;

6 mV

3. Biểu thức hàm truyền TBB theo góc liệng

Thực chất mặt phẳng liệng được hình thành khi xuất hiện yêu cầu cơ động TBB đồng thời trong 2 mặt phẳng gật và hướng, tức là khi đồng thời

cb và 0. Mặt phẳng liệng là hai mặt phẳng điều khiển ban đầu (gật và

hướng) được xoay đi một góc liệng  quanh trục dọc TBB (xem hình 4.28).

Y

Ycos

YE



Z=Ysin

G=mg

YE

V

X1X



P

Z

X Hình 4.28 Điều khiển đổi hướng đối với TBB

Zđk

cánh phẳng



a. Đổi hướng phẳng; b. Đổi hướng kiểu liệng.

y

- Biến đổi Laplace phương trình mômen với điều kiện bỏ qua mômen nhiễu:

X

p2J

1

 mEqS

X

C

1

d.E

 mxqS

X

1

2

d

C 2V p

 mxqS d2

mEqS d

(4.22)

E

 p2 X1 Cp(p) X1 C

(p)



X



 2J V 

1

JX1

mxqS d2

nếu đặt:

c X1 C

là hệ số cản khí động trong chuyển động liệng;

X

1 2J V

1

mEqS d

c X1 C

3 J

là hệ số hiệu quả cánh lái Eleron.

Ta có:

X1

pp  c (p)  c 

(p)

(4.23)

1 3 E

- Biểu thức hàm truyền rút ra từ (4.23):

K (p) 

(p)  c3

 K

(4.24)



E

(p)

p(c1

 p)

p(1 pT)

Trong đó:

K c3 / c1

là hệ số truyền;

T 1/ c1

là hằng số thời gian

xác định quán tính TBB theo điều khiển liệng.

4.5.2 Cấu trúc các kênh điều khiển và ổn định định hướng TBB

Đối với TBBKNL có sơ đồ khí động kiểu cánh phẳng, hệ thống điều khiển trên khoang gồm có 3 kênh gật, hướng và liệng tương ứng với ba góc Ơ-le. Căn cứ trên các thuật toán điều khiển, hàm truyền của TBB và các phần tử như AP, máy lái và các phần tử hiệu chỉnh, ta có thể xây dựng được sơ đồ cấu trúc của các kênh điều khiển và ổn định định hướng [11, 37].

1. Cấu trúc của kênh gật điều khiển - ổn định độ cao

Kênh điều khiển - ổn định độ cao làm việc theo 2 chế độ:

- Chế độ điều khiển, khi trình bay theo độ cao.

K  KH(H)  0 . Tức là khi thay đổi chương

- Chế độ ổn định độ cao bay, khi

K cb

 const.

(=0, hướng vector

vận tốc song song với mặt phẳng nằm ngang).

T2 p

K





1

(p)

KTBB (1  TV )



1  T p

1  T p

ML

p(1  2 T p  T p2 )

2

1

TBB TBB TBB

(p)

KH

K AP

(H)

Hình 4.29 Sơ đồ cấu trúc kênh điều khiển gật

Trong đó:

KH là khâu biến đổi lệnh thành tín hiệu tỷ lệ với góc gật yêu cầu;

KAP là hệ số truyền khối tự lái,

KAP k0

theo biểu thức (1.8);

vào;

1

1  T1p

là khâu giữ chậm trong AP hạn chế tác động thăng giáng đầu

góc;

T2  k1 / k0

suy từ (1.8), đặc trưng cho quán tính của cảm biến vận tốc

1

1  TML p

hàm truyền khâu truyền động lái (máy lái) trong kênh.

2. Cấu trúc của kênh điều khiển - ổn định hướng

T2 p

K 

AP

K



1  (p)

Z

TBB V

K' (1  T' )

1  T p

1  T p

p(1  2' T'

p  T' p2 )

2



1

ML

TBB TBB

TBB

(p)

KZ

(Z)

Hình 4.30 Sơ đồ cấu trúc kênh điều khiển hướng

Trong đó các khâu thuộc AP và máy lái có chức năng và tham số giống như trong kênh gật, riêng khâu biến đổi KZ là biến đổi lệnh thay đổi tọa độ Z thành tín hiệu tỷ lệ với góc đổi hướng yêu cầu;

Tương tự như kênh điều khiển - ổn định độ cao, kênh điều khiển - ổn định hướng cũng làm việc theo 2 chế độ chính.

- Chế độ điều khiển, khi

K  KZ(Z) 0 . Tức là khi thay đổi hướng

so với hướng ban đầu theo chương trình bay.

- Chế độ ổn định hướng, khi

K 0  const.

3. Cấu trúc của kênh điều khiển liệng

Sơ đồ cấu trúc của các kênh điều khiển liệng được xây dựng trên hình





к

K

sinK

Con quay

My

Ky

1

H

1

p

4.31.

к



K

1

E

K



cq

1  T p

1  T p

1 

p



ML





sin

Hình 4.31 Sơ đồ cấu trúc kênh điều khiển liệng TBB

Sơ đồ cấu trúc được xây dựng trên cơ sở các thuật toán điều khiển liệng, hàm

truyền phần tử đo vận tốc thay đổi góc liệng theo nguyên lý con quay hai bậc tự do, hàm truyền máy lái kênh liệng và bản thân TBB.

4.5.3 Phương pháp ghép bộ đo VTG với các kênh điều khiển TBB

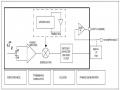
Căn cứ vào mô hình toán học phép đo VTG theo VTT, mô hình bộ lọc tối ưu các thành phần VTG, kết quả thực nghiệm và cấu trúc các kênh điều khiển - ổn định góc định hướng của TBB ta có thể xây dựng được sơ đồ phối ghép bộ đo các thành phần VTG theo VTT với các kênh điều khiển như sau.

MÁY TÍNH TRÊN KHOANG

Biến đổi ADC và thuật toán lọc tối ưu VTG

*x1; *y1; *z1

Thuật toán xác định tọa độ góc

, , 

prog;prog;pro

Th/t tạo lệnh

- Lệnh 

- Lệnh 

- Lệnh 

















Th/t tạo th/số ĐK

- So sánh ,,

- Tính các đạo hàm

’, ’, ’

Kênh điều khiển - ổn định góc gật

(sơ đồ cấu trúc 4.29)

Cảm biến VTT (HMC-2003)

- Cảm biến H1x

- Cảm biến H1y

- Cảm biến H1z

Cảm biến bổ sung

- Gyro MEMS 1y

Kênh điều khiển - ổn định hướng

(sơ đồ cấu trúc 4.30)

Kênh điều khiển - ổn định liệng

(sơ đồ cấu trúc 4.31)



Hình 4.32 Sơ đồ phối ghép hệ đo góc và VTG với các kênh điều khiển TBBKNL

Kết luận chương 4

Từ những nội dung của chương 4, có thể rút ra những kết luận sau:

1. Đã chứng minh được khả năng thực tế hóa bộ đo các thành phần VTG theo VTT trong hệ TĐLK của TBB. Tính đầy đủ của vấn đề cần chứng minh được thể hiện cụ thể qua: lựa chọn vật tư linh kiện; thiết kế, tổ chức phần cứng; tổ chức, xây dựng các chương trình phần mềm thử nghiệm; đối chiếu

tính ưu việt của những phương án (mô hình) xử lý thông tin và những phân tích kết quả thu được từ thực nghiệm.

2. Những kết quả thực nghiệm đã phản ánh trung thực các kết quả mô phỏng theo những phương án lọc – xử lý thông tin đo VTG bằng VTT đã thực hiện trong chương 3. Từ đó cho phép ta lựa chọn mô hình tối ưu của một bộ đo VTG theo thông tin VTT Trái đất, đó là bộ lọc MS-AUKF có chất lượng cao hơn hẳn so với các mô hình còn lại. Bộ lọc này không những đáp ứng được tính chất phi tuyến của hệ đo trong dải rộng, mà còn thích nghi được với những điều kiện bất định của nhiễu tạp trong quá trình sử dụng.

3. Trong chương 4 còn có thêm đề xuất nâng cao chất lượng của bộ đo phụ thuộc điều kiện cảm biến VTG, bổ sung thông tin cho hệ thống, có chất lượng không cao. Đề xuất này đã được thực tế hóa bằng những thuật toán lọc bias đầu ra cảm biến và chứng tỏ cải thiện được đáng kể độ chính xác đo.

4. Từ kết quả phân tích, tổng hợp các thuật toán đo – xử lý thông tin từ trường ở chương 3, kết quả thực nghiệm và cấu trúc các kênh điều khiển - ổn định ở chương 4, cho phép ta xây dựng một hệ thống ĐKĐH cho TBBKNL như mô tả trên sơ đồ hình 4.32.

Từ bốn kết luận trên có thể đánh giá nội dung thực nghiệm của luận án đã đạt được mục đích đề ra là kiểm tra khả năng hiện thực hóa những vấn đề lý thuyết đã nghiên cứu ở chương 2 và 3 thành thiết bị đo VTG và điều khiển ổn định định hướng không gian cho TBBKNL theo một phương án tối ưu.